总结
在考场上因为看到这题时没多少时间了,草草的看了下题,就开始了数据结构暴力搞,后来发现要在递归里套递归,就放弃了(逃)。考后在吸收了他人的经验之后,前来补上。
这题刚看有点像数据结构,但经过仔细分析后,其实不是。它只需要单点修改和区间乘(如果真是数据结构,不至于这样);
如果我们把每个操作看作一个点,把每个类型为(3)的操作与它之后要调用的函数连一条边,再加上题目说了不会之间或间接的调用自己,即无环,那么它就是一个(DAG)。对于(DAG),那就有很多可以操作的了。
从题目入手,若操作为类型(1),及只需对某一个元素进行修改即可,若在它之后有类型为(2)的操作,将整个数列乘上(k),那么可以理解为这个类型为(1)的操作被执行了(k)次。那么,我们需要求出每个单点加的操作之后有多少个乘的操作,共乘了多少倍,记为(sum),仔细想一下,倒着来会好一些,因为我们不可能对于每个操作都单独去求一次(sum),所以肯定是一遍从后往前求,因为你后面求(sum)的对于前面的而言,也是需要的,前面求的又不会影响到你后面的。
至于顺序,就按着它给出的操作顺序倒着来。
然后对于每个操作在执行后会有多少乘积累加,我们用用拓扑序倒序来求,反正它都已经是个(DAG)了,记为(mul),在求(sum)前求出来。
不过需要注意的是,在你求出(mul)和(sum)之后,还需要将(sum)下放,
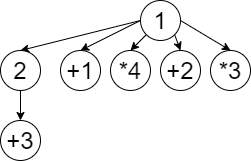
就拿这个图来说,我们假设(1)节点的(sum)为(x),那么(+2)这个操作的(sum)应格外增加(3x),同理(+1)的(sum)应增加(12x)。(好像没搞很懂)
所以下传(sum)时,假设一个节点(x)的(sum)为(S),儿子为(y),从(1)到(k)编号,那么(y_i)的(sum)就应该增加
[S imes prodlimits_{j={i+1}}^kmul_j
]
最后遍历一遍即可。
代码:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+7;
const int mod=998244353;
#define NEKO puts("NEKO")
#define ll long long
#define il inline
#define vocaloid(v) (v>='0'&&v<='9')
template <typename T>
il void read(T &x)
{
x=0;int flag=1;char v=getchar();
while(!vocaloid(v)) {if(v=='-') flag=-1;v=getchar();}
while(vocaloid(v)) {x=(x<<1)+(x<<3)+v-'0';v=getchar();}
x*=flag;
}
template <typename T>
il void write(T x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
struct miku{
int v,next;
}MIKU[maxn<<1];
struct Alone{
int tp,pos;
ll mul,sum,val;
}b[maxn];
ll a[maxn];
int n,m,Q,cnt,ord[maxn];
int h[maxn],in[maxn],opt[maxn],rin;
queue<int>q;
il void add(int u,int v)
{
MIKU[++cnt].next=h[u];
MIKU[cnt].v=v;
h[u]=cnt;
}
il void topo()
{
for(int i=1;i<=m;i++)
if(!in[i]) q.push(i);
while(!q.empty())
{
int x=q.front();q.pop();
opt[++rin]=x;
for(int i=h[x];i;i=MIKU[i].next)
{
int v=MIKU[i].v;
in[v]--;
if(!in[v]) q.push(v);
}
}
}
il void dfs()
{
for(int i=m;i>=1;i--)
{
int x=opt[i];
for(int j=h[x];j;j=MIKU[j].next)
{
int v=MIKU[j].v;
b[x].mul=b[x].mul*b[v].mul%mod;
}
}
}
il void down()
{
for(int i=1;i<=m;i++)
{
int x=opt[i];ll now=1;
for(int j=h[x];j;j=MIKU[j].next)
{
int v=MIKU[j].v;
b[v].sum=(b[v].sum+b[x].sum*now%mod)%mod;
now=now*b[v].mul%mod;
}
}
}
int main()
{
read(n);
for(int i=1;i<=n;i++) read(a[i]);
read(m);
for(int i=1;i<=m;i++)
{
read(b[i].tp);
if(b[i].tp==1)
read(b[i].pos),read(b[i].val),b[i].mul=1;
else if(b[i].tp==2)
read(b[i].val),b[i].mul=b[i].val;
else
{
int x;read(b[i].pos);b[i].mul=1;
for(int j=1;j<=b[i].pos;j++)
{
read(x);add(i,x);
in[x]++;
}
}
}
topo();dfs();
read(Q);ll now=1;
for(int i=1;i<=Q;i++) read(ord[i]);
for(int i=Q;i>=1;i--)
{
int x=ord[i];b[x].sum=(b[x].sum+now)%mod;
now=now*b[x].mul%mod;
}
down();
for(int i=1;i<=n;i++) a[i]=a[i]*now%mod;
for(int i=1;i<=m;i++)
if(b[i].tp==1)
a[b[i].pos]=(a[b[i].pos]+b[i].val*b[i].sum%mod)%mod;
for(int i=1;i<=n;i++) write(a[i]),printf(" ");
return 0;
}