数据结构学习-第一次总结

数据结构学习-第一次总结

1.思维导图

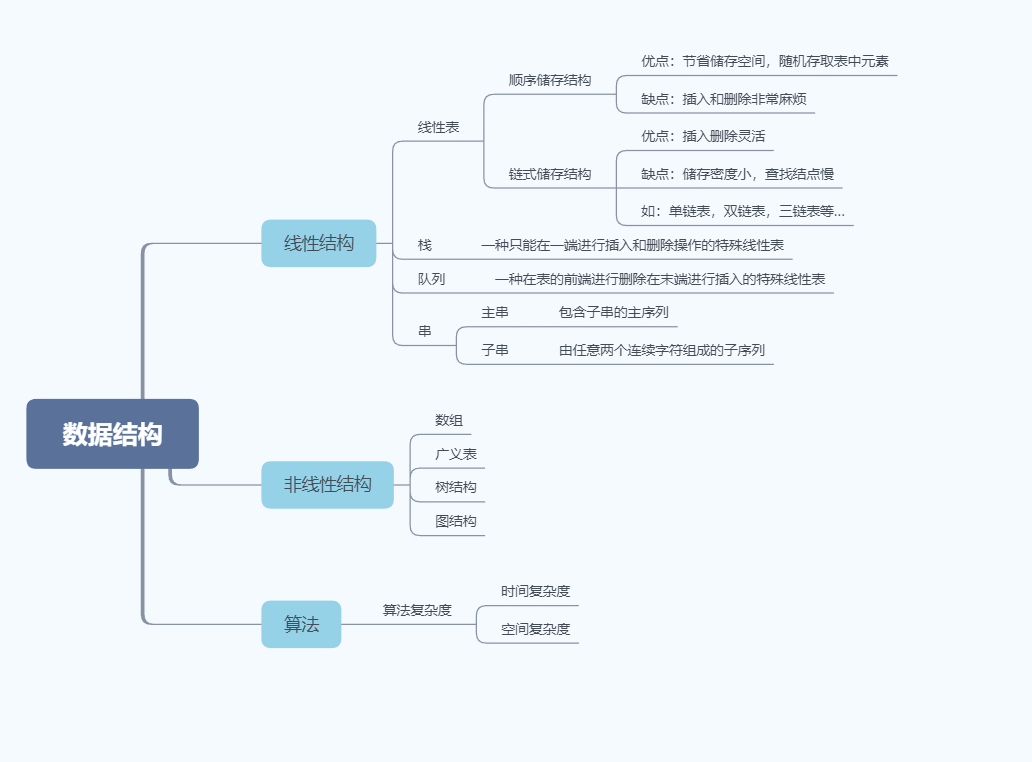
2.学习笔记

线性表

1. 线性表定义： 具有相同特性的数据元素的一个有限序列。
2. 线性表的顺序存储结构 ：使用一块地址连续的存储空间，按照线性表中元素的逻辑顺序依次存放相应元素。
3. 顺序存储结构的特点： 1. 逻辑上相邻，物理地址相邻 2. 实现随机存储（快速访问）
4. 顺序表的基本操作-插入 ：要在第i个位置插入e，须将i到n之间的元素往后移
   代码演示：

bool ListInsert(SqList *&L, int i , ElemType e){
   if (i<1 || i>L->length+1)
      return false; //删除位置不合法
   i--; //将顺序表逻辑序号转化为物理序号
   for(int j=L->length;j>i ;j--) //将data[i..n]元素后移
      L->data[j]=L->data[j-1];
   L->data[i]=e; //在i位置插入元素e
   L->length++; //顺序表长度增1 return true;
 } 

5. 顺序表的基本操作-删除 代码演示：

bool ListDelete(SqList *&L, int i, ElemType &e){
  if (i<1 || i>L->length) //删除位置不合法
      return false;
  i--; //将顺序表逻辑序号转化为物理序号
  e=L->data[i];
  for(int j=i; j<L->length-1;j++)//将data[i..n-1]元素前移
      L->data[j]=L->data[j+1];
  L->length--; //顺序表长度减1
  return true;
} 

6. 线性表的链式结构 ：线性表中的数据元素存放在一组地址任意的存储节点，节点之间使用“链”进行连接。

   节点 = 数据元素 + 指针
   数据元素：存放数据
   指针：存放该节点下一个元素的存储位置

7. 线性表的链式结构

   头指针：指向线性表的第一个元素a1
   头节点：为了简化插入与删除操作，需要在第一个节 点之前设置一个头节点

8. 存储密度 = 数据所占空间 / 节点所占用空间
9. 创建链表：

   头插法
   尾插法

10. 其它链表：双链表，循环链表，双向循环链表。

栈和队列

1. 栈：是限制仅在线性表的一端进行插入和删除运算后进后出（LIFO）的线性表。
   队列：是一种先进先出(FIFO) 的 线性表. 在表一端插入，在另一端删除。
2. 栈的进栈出栈规则：

按序进栈→有n个元素1，2，…,n，它们按1,2, …, n的次序进栈。
栈顶元素先出栈→栈底元素最后出栈；
时进时出→元素未完全进栈时，即可出栈。

3. 链栈无需附加头节点。
4. 栈的应用：

   数制转换
   括号匹配检验
   表达式转换
   迷宫问题

5. 符号配对问题求解：
   部分代码展示：

#include<iostream>
using namespace std;
#include<stack>
#include<queue>
#include<string>
#include<cstring>

int main ( )
{
    char str[100], *p;
    p = str;
    cin >> p;
    int len = strlen( str );
    int i = 0;
    stack<char>Stack;
    queue<char>Queue;
    for(i = 0; i < len; i++){
        if (p == '＋' || p == '-' || p == '*' || p == '/' || p == '↑'){
            Stack.push( p[i] );
         }
    }
    for(i = 0; i < len; i++){
        if(p>=A&&p<=Z) Queue.push( p[i] );
    }
    while (!Stack.empty()) {
        if (Stack.top() != s) {
	Queue.push(Stack.top());
        }
        Stack.pop();
    }
    while (!Queue.empty()) {
        cout << Queue.front();
        Queue.pop();
    }

    return 0;
}

6. 递归：一个直接调用自己或通过一系列的调用语 句间接地调用自己的函数。
7. 递归的两大特点：

   1.自我调用
   2.必须有递归出口

8. 队列详解：

   InitQueue(&Q) 操作结果：构造一个空队列Q。
   DestroyQueue(&Q) 操作结果：队列Q被销毁，不再存在。
   QueueEmpty(Q) 操作结果：若Q为空队列，则返回TRUE，否则返回 FALSE
   QueueLength(Q) 操作结果：返回Q的元素个数，即队列的长度。
   GetHead(Q, &e) 操作结果：用e返回Q的队头元素。
   等...

9. 队满和队空判断条件：front-队头指针 rear-队尾指针

   队空：Q.rear = Q.front
   队满：(Q.rear+1) % m = Q.front

字符串

1. 串---由零个或多个字符组成的有限序列。
2. 空串：包含零个字符， 即长度为零的串称为空串。
   子串：串中任意个连续的字符组成的子序列。
   主串：包含子串的串称为主串。
   位置：字符在序列中的序号。
   相等：两个串的长度相等，并且对应位置的字符 都相同。
3. 串的模式匹配算法：

   BF算法 特点：指针不停的回溯，时间复杂度不定，较高。
   KMP算法 特点：主串不需回溯i指针，将模式串向右“滑动”尽可能远的一段距离。

4. KMP算法，主串上的i为什么无需回溯？

   主串S: abcabcac //S串上指针为I
   模式串T: abcac //T串上指针为j
   如果i回溯到3,j回溯到1，那么S[3..4]与T[1..2]一 样，继续比较起来才有意义。既然S[3..4]与T[1..2]一 样，那么直接拿S[5]与T[3]比较即可，即i无需回溯到 i=3。同理i也无需回溯到4。

5. next[j]函数和nextval[j]函数：

   定义next[j]函数，表示当模式中第j个字符与主串中 字符x“失配”时。x下回
   应和模式串中的第next[j]个字符进行比较。
   nextval函数代码演示：

void get_nextval(SString &T, int &nextval[]) {
   i = 1; nextval[1] = 0; j = 0;
   while (i < T[0]) {
      if (j=0 || T[i]==T[j]) {
         ++i;  ++j;
         if (T[i] != T[j])  nextval[i] = j;
         else  nextval[i] = nextval[j];
       }
       else  j = nextval[j];
    }
 } // get_nextval

3.疑难问题：next值，nextval值的计算。

KMP算法的复杂性以及对next和nextval函数认识的不全导致计算混乱。

详细分析：

next数组的求解方法是：第一位的next值为0，第二位的next值为1，后面求解每一位的next值时，根据前一位进行比较。首先将前一位与其next值对应的内容进行比较，如果相等，则该位的next值就是前一位的next值加上1；如果不等，向前继续寻找next值对应的内容来与前一位进行比较，直到找到某个位上内容的next值对应的内容与前一位相等为止，则这个位对应的值加上1即为需求的next值；如果找到第一位都没有找到与前一位相等的内容，那么需求的位上的next值即为1。
举例： 序号： 1 2 3 4 5
字符串：a b a c a
next值：0 1 1 2 1
nextval值：0 1 0 2 0

• 前两位next始终为 0 1；

• 求第三位next值时看前一位（序号为2）b（都和这个b比较），它的next值为1，则看序列号为1对应是a与b不相同，没有再之前的数，所以第三位next值是1

• 求第四位next值时看前一位（序号为3）a（都和这个a比较），它的next值为1，则看序列号为1对应是a与a相同，所以第三位next值是1 +1=2

• 求第五位next值时看前一位（序号为4）c（都和这个c比较），它的next值为2，则看序列号为2对应是b与c不相同，接着看b的next值为1对应序列号为1的是a，a与c不相同。到头都没有相同的,则next值是1

求nextval值

• 第一位nextval为0，第二位如果与第一位相同则为0，如果不同则为1

• 第三位a的next值为1，找到序号1对应字符串为a，相同则把序号一的next值给第三位的nextval是0

• 第四位c的next值为2，找到序号2对应字符串为b，不相同保留当年next值到nextval还是2

• 第五位a的next值为1，找到序号1对应字符串为a，相同则把序号一的next值给第三位的nextval是0