用例:
将一组数据从大到小进行排列 10, 16, 18, 12, 11, 13, 15, 17, 14, 19
size=10
步骤1.根据数组初始化堆中的数据(无序堆)
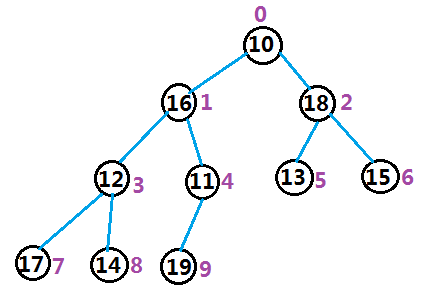
步骤2.从最后一个根节点( 下标为(size-1-1)/2 )开始往第一个根节点遍历,依次将每个最小子树排好序,建造一个小堆:
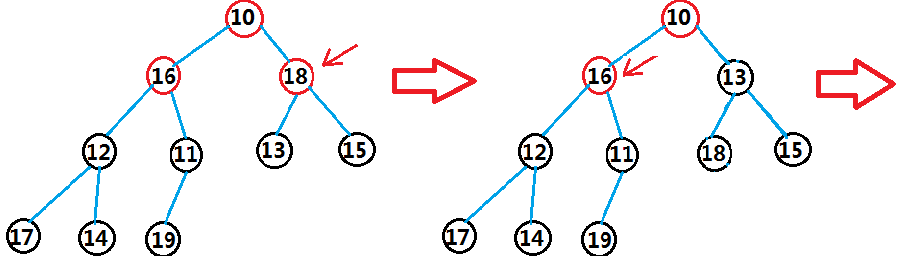

步骤3.进行堆排序:将堆数组的首位置和末位置的数据交换,缩小范围 以--size大小的范围将堆顶数据下调,完成建堆


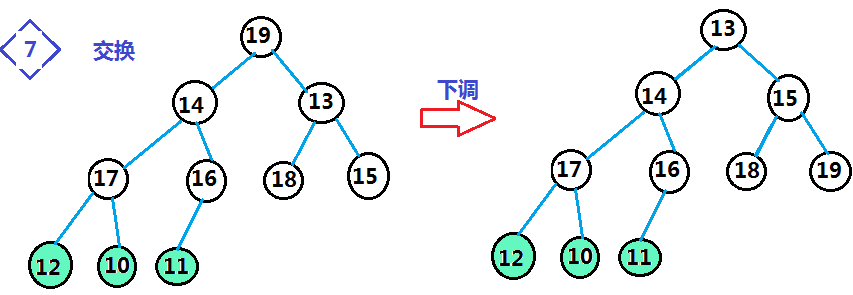
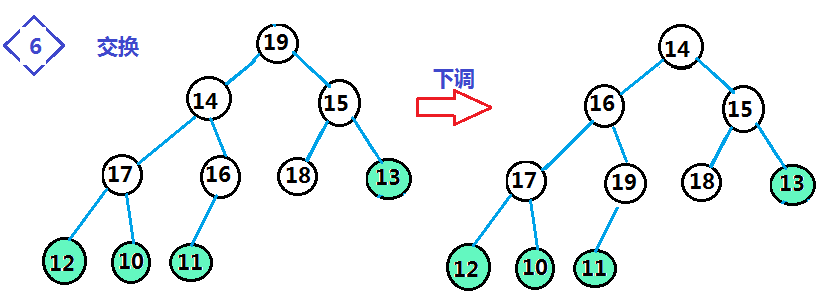
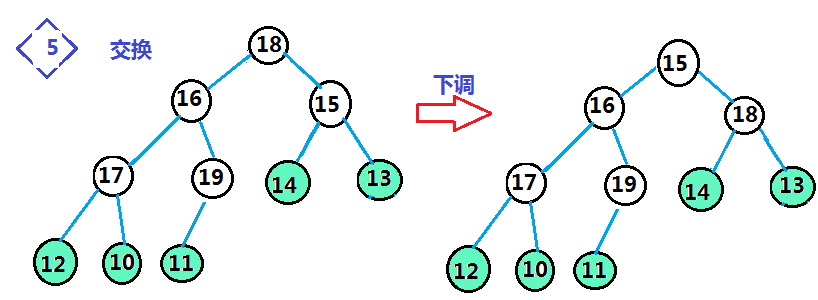
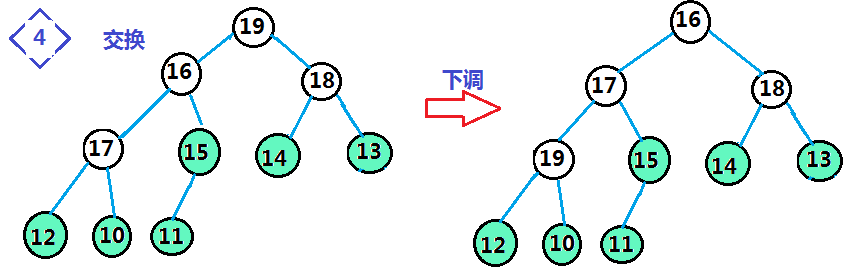
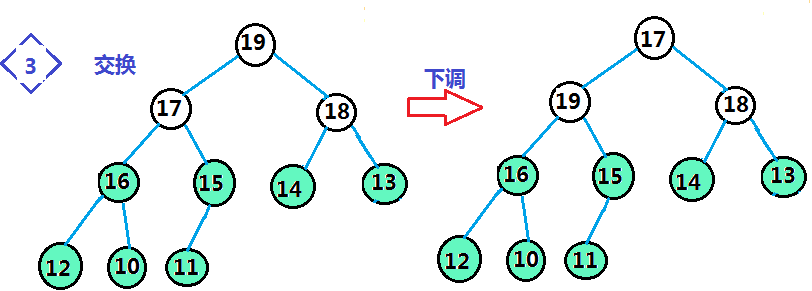
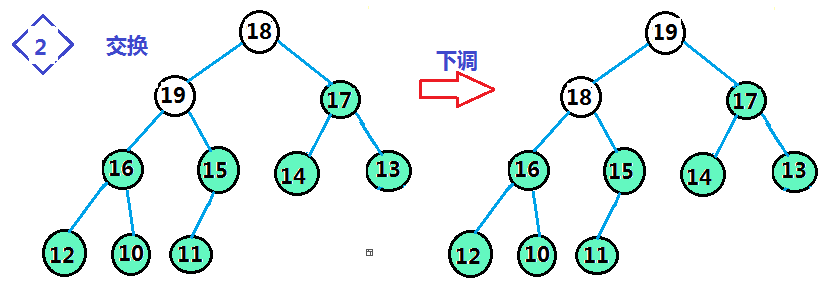

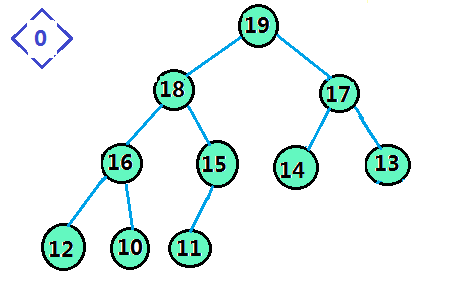
理解了整个思想,我们就来看代码:
先实现一个下调函数用来建堆,并对堆进行调整:(本案例是从大到小进行排序,所以建的是小堆;若是要从小到大进行排序,则要按照大堆思想进行实现,对代码稍微进行改进即可)
//下调
void AdjustDown(int *array, int parent, int size)
{
int left = parent * 2 + 1;
int right = left + 1;
while (left < size)
{
// 比较左右孩子,保证下标left为最小的节点下标
if (right <size && array[right] < array[left])
{
left = right;
}
// 如果父节点大于左右孩子中较小的节点时,就交换这两个节点,要保证两个子节点都大于父节点
if (left<size && array[parent]>array[left])
{
// 交换之后还需继续 将相对较大的数循环向下调
swap(array[left], array[parent]);
parent = left;
left = parent * 2 + 1;
right = left + 1;
}
else
{
break;
}
}
}
堆排序:按照图说的步骤来写代码,首先要初始化一个堆数组并对它进行排序,之后再一步步将堆顶与有效堆尾数据进行交换,并逐渐缩小堆的size,一组有序的数据就排好了!
//堆排序
int* HeapSort(int *heap, int size)
{
for (int start = (size - 1 - 1) / 2; start >= 0; start--)
{
AdjustDown(heap, start, size);
}
for (int i = size - 1; i >= 0; --i)
{
swap(heap[0], heap[i]);
AdjustDown(heap, 0, i);
}
return heap;
}