1.1 适用情况
该算法用于解决一个数组/链表中是否存在环的情况!
1.2 复杂度
时间复杂度:O(n)
空间复杂度:O(1)
1.3 判断是否存在环
核心思想:类似于龟兔赛跑的原理,使用一个快指针和一个慢指针,快指针一次走两步,慢指针一次走一步,若数组/链表中存在环,那么快慢指针一定会在某一时刻指向同一个元素;
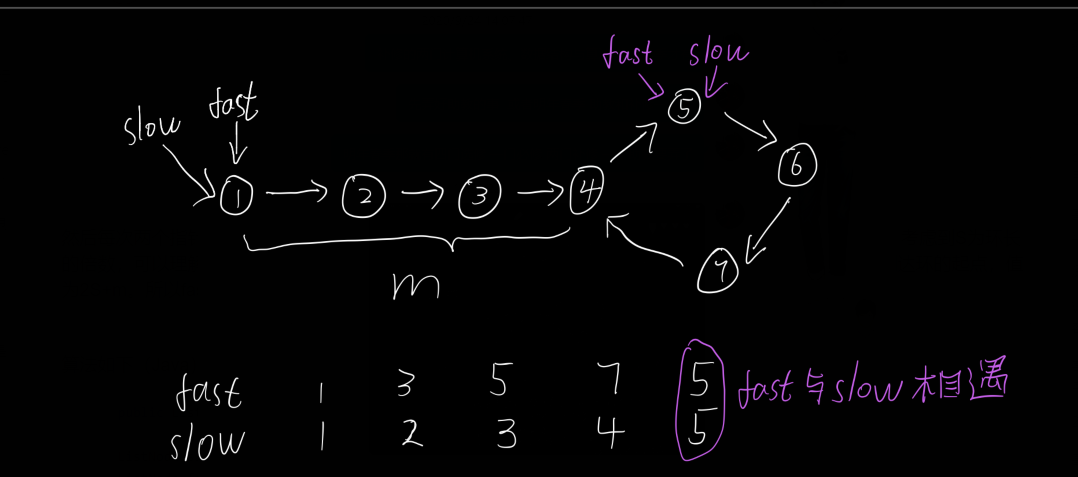
fast指针走过的路程 Sfast=m+n1*k+c
slow指针走过的路程 Sslow=m+n2*k+c
假设Sslow=s,因为快指针一次走两步,慢指针一次走一步,那么Sfast=2s;
其中:
m为起点至环入口的距离;
k为环的长度;
n为指针绕着环转的圈数;
c为最后位置距环入口的距离
那么Sfast-Sslow = 2s - s = (n1-n2)*k = s,即两个指针的走过的总路程相差若干个环的长度,也可以说明慢指针走过的路程刚好等于环的长度的整数倍(在1.4 验证);
所以,当fast指针和slow存在指向同一个元素(非第一个)的情况时,我们就可以认为它存在环;
1.4 找到环的入口
在1.3中我们以及证明了慢指针走过的路程刚好等于环的长度的整数倍,下面我们来验证下:
从图中可以看出慢指针从0开始,走了4步到达相遇的地点,而换的长度刚好是4,这不是特例,任何图都是这样;
那么如何才能找到环的入口呢?
我们现在知道fast指针走了2s的距离,我们只需要加上m就可以刚好走到环的起始点;这样fast指针所走的路程Sfast=2s+m,相当于fast从起点走了m步到达环的入口,再围着环饶了若干圈后又回到了环的入口处,所以现在的主要问题就是怎样得到这个m;
有这样一个策略:我们把slow指针丢到起点,而fast不变位置,现在开始他俩每次都只走一步,那么一定存在这样一种情况,slow指针走了m步到达环的入口时,fast也走了m步到达了环的入口,那么此时它俩都指向环的入口,自然就能确定环的入口了;
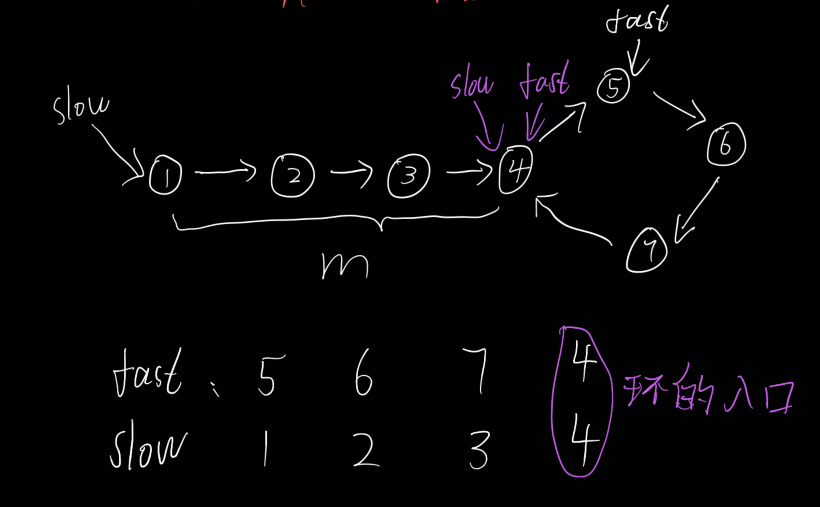
1.5 代码实现
Leetcode中应用此算法的题:环形链表 以及 寻找重复数
链表的实现可参考文章:算法-floyd判环(圈)算法
数组的实现:
int findDuplicate(vector<int> &nums)
{
int len = nums.size();
int fast = 0, slow = 0;
while (nums[slow] != nums[fast] || fast == 0)
{
slow = nums[slow];
fast = nums[nums[fast]];
}
//此时fast和slow处于同一位置,并在环中
//置slow=0
slow = 0;
while (nums[slow] != nums[fast])
{
slow = nums[slow];
fast = nums[fast];
}
return nums[fast];//返回环起始处的元素
}