一、高斯混合模型概述
1、公式
高斯混合模型是指具有如下形式的概率分布模型：
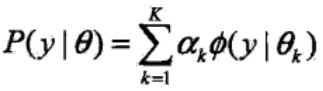
其中，αk≥0，且∑αk=1，是每一个高斯分布的权重。Ø(y|θk)是第k个高斯分布的概率密度，被称为第k个分模型，参数为θk=(μk, αk2)，概率密度的表达式为：
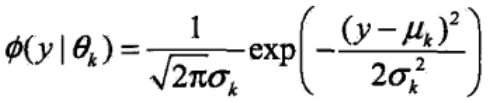
高斯混合模型就是K个高斯分布的线性组合，它假设所有的样本可以分为K类，每一类的样本服从一个高斯分布，那么高斯混合模型的学习过程就是去估计K个高斯分布的概率密度Ø(y|θk)，以及每个高斯分布的权重αk。每个观测样本出现的概率就表示为K个高斯分布概率的加权。
所谓聚类，就是对于某个样本yj，把该样本代入到K个高斯分布中求出属于每个类别的概率：
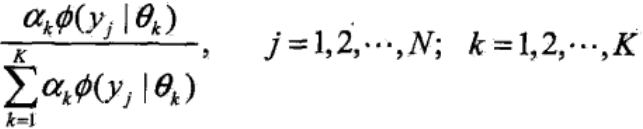
然后选择概率值最高的那个类别作为它最终的归属。把所有的样本分别归入K个类，也就完成了聚类的过程。
2、案例
假设有 20 个身高样本数据，并不知道每个样本数据是来自男生还是女生。在这种情况下，如何将这 20 个身高数据聚成男女生两大类呢？
用高斯混合模型来聚类，那么假设男女生身高分别服从两个不同的高斯分布，高斯混合模型就是由男生身高和女生身高这两个高斯分布混合而成。在高斯混合模型中，样本点属于某一类的概率不是非0即 1 的，而是属于不同类有不同的概率值。如下图，有两个高斯分布，均值分别为μ1和μ2，而高斯混合模型就是又这两个高斯分布的概率密度线性组合而成。
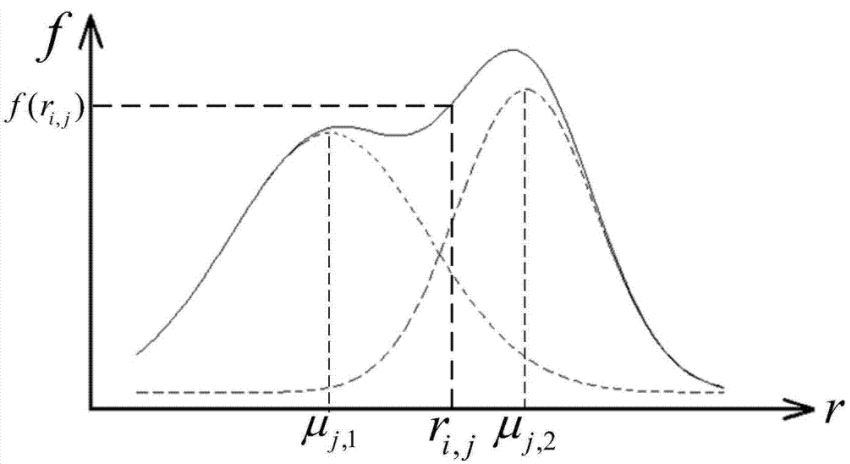
二、高斯混合模型参数估计的EM算法
假设观测数据y1, y2, ...yN由高斯混合模型生成：
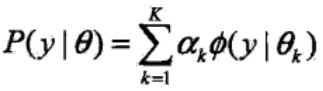
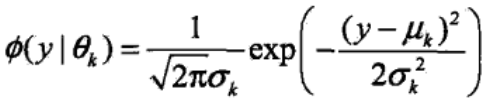
其中，要估计的参数θ=(α1, α2, ...αK; θ1, θ2, ..., θK)，θk=(μk, αk2)，k=1,2,...,K。因此如果高斯混合模型由K个高斯分布混合而成，那么就有3K个参数需要估计。
我们用极大似然估计法来估计参数θ，也就是求参数θ，使得观测数据y的对数似然函数L(θ)=logP(y|θ)的极大化：
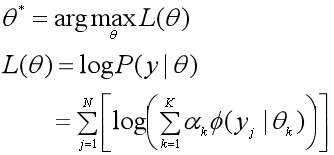
由于对数似然函数L(θ)中包含了和的对数，比较难以求解，因此考虑用EM算法。
（一）高斯混合模型EM算法的推导
用EM算法估计高斯混合模型的参数θ，步骤如下：
1、明确隐变量，写出完全数据的对数似然函数
可以设想观测数据yj，j=1,2,..., N，是这样产生的：
首先依概率αk选择第k个高斯分布分模型Ø(y|θk)，然后依这个分模型的概率分布Ø(y|θk)生成观测数据yj，N个观测数据中有多个来自于同一个分模型。
这时观测数据yj，j=1,2,..., N是已知的，而反映观测数据yj来自于第k个分模型的数据是未知的，也就是隐变量，用γjk表示：
有了观测数据yj和未观测数据γjk，那么完全数据是：
在《概率图模型之EM算法》中，我们说了，EM算法的目标是通过迭代，求不完全数据的对数似然函数L(θ)=logP(y|θ)的极大似然估计，这可以转化为求完全数据的对数似然函数logP(y, γ|θ)的期望的极大似然估计。
于是我们先得到完全数据的似然函数：
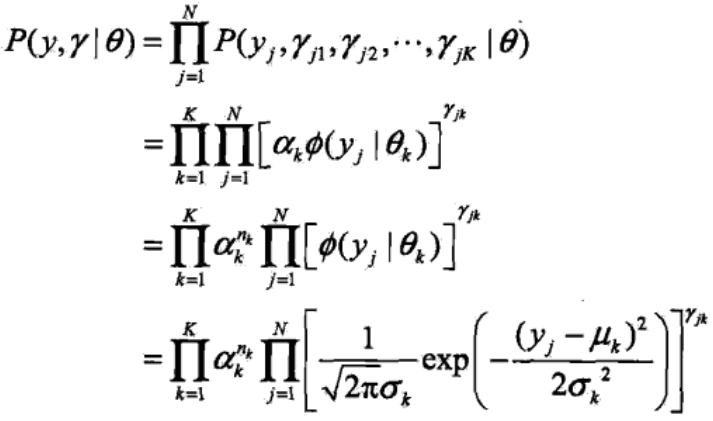
其中nk表示N个观测数据中，由第k个分模型生成的数据的个数。
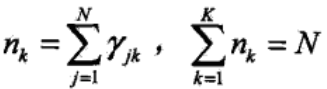
那么完全数据的对数似然函数为：
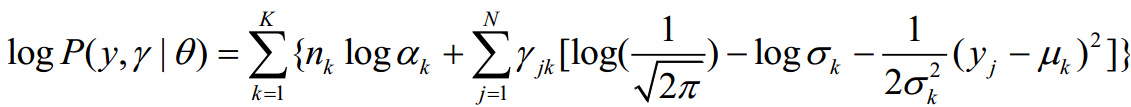
2、EM算法的E步：确定Q函数
Q函数是指，在给定观测数据y和第i轮迭代的参数θ(i)时，完全数据的对数似然函数logP(y, γ|θ)的期望，计算期望的概率是隐随机变量γ的条件概率分布P(γ|y, θ(i))。于是Q函数为：
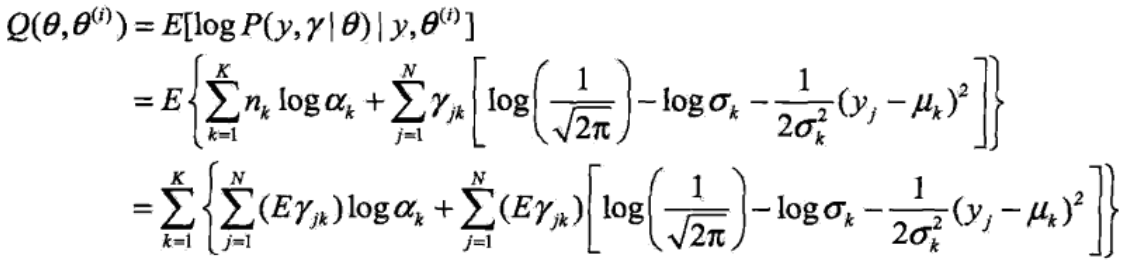
其中隐随机变量γ的条件概率分布P(γ|y, θ(i))为：
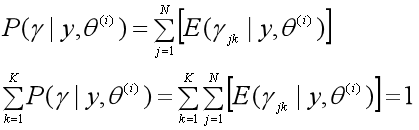
这里需要计算E(γjk|y, θ(i))：
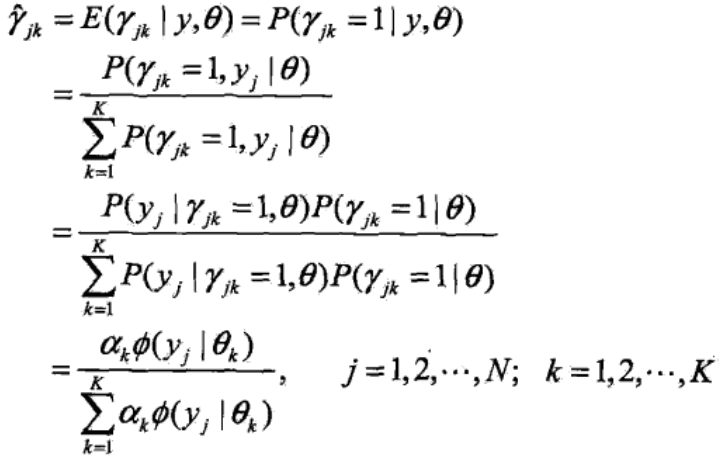
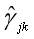是当前模型参数θ(i)下第j个观测数据来自第k个分模型的概率，称为分模型k对观测数据yj的响应度。
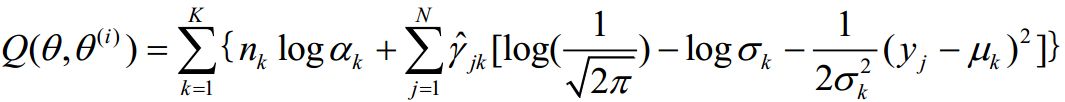
3、确定EM算法的M步：
M步也就是在得到第i轮的参数θ(i)之后，求下一轮迭代的参数θ(i+1)，使函数Q(θ,θ(i))极大：
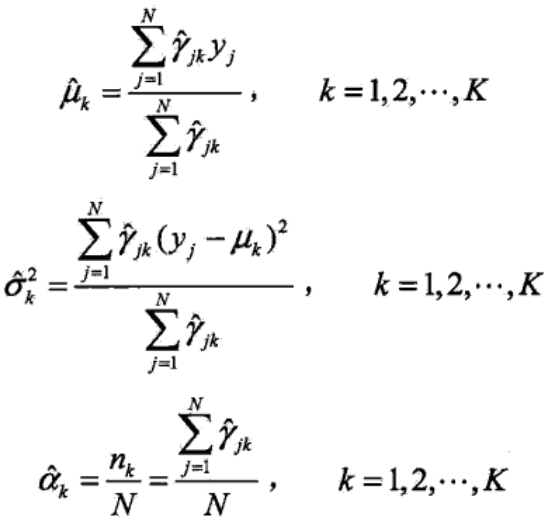
得到参数θ(i+1)之后，继续进行迭代求新的参数，直到Q函数的值不再有明显变化为止。
（二）高斯混合模型EM算法总结
输入：观测数据y1,y2,...,yN，和高斯混合模型：
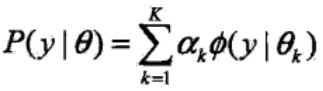输出：高斯混合模型的参数θ=(α1, α2, ...αK; θ1, θ2, ..., θK)，θk=(μk, αk2)，k=1,2,...,K。
步骤：
1、取参数的初始值开始迭代；
2、E步：在第i轮迭代过后，根据当前的模型参数θ(i)，求高斯分布分模型Ø(y|θk)对观测数据yj的响应度：
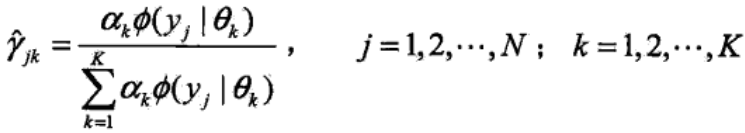
3、M步：计算新一轮迭代的模型参数：
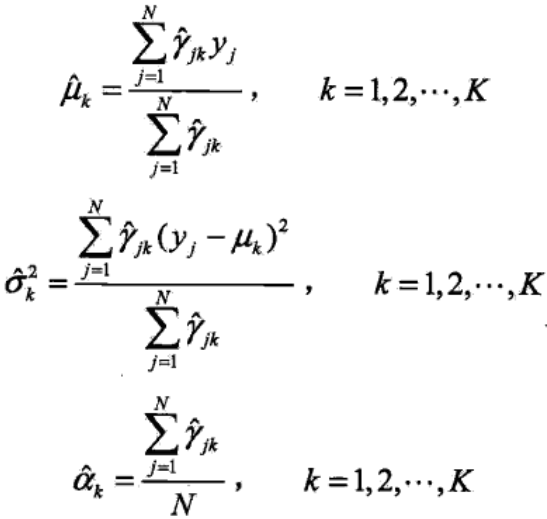
4、重复第2步和第3步，直到收敛而停止迭代。停止迭代的条件是，对于较小的正数ε1、ε2，有：
参考资料：
李航：《统计学习方法》