AB跳过,B实在没心情改了
Nadeko's birthday is approaching! As she decorated the room for the party, a long garland of Dianthus-shaped paper pieces was placed on a prominent part of the wall. Brother Koyomi will like it!
Still unsatisfied with the garland, Nadeko decided to polish it again. The garland has n pieces numbered from 1 to n from left to right, and the i-th piece has a colour si, denoted by a lowercase English letter. Nadeko will repaint at most m of the pieces to give each of them an arbitrary new colour (still denoted by a lowercase English letter). After this work, she finds out all subsegments of the garland containing pieces of only colour c — Brother Koyomi's favourite one, and takes the length of the longest among them to be the Koyomity of the garland.
For instance, let's say the garland is represented by "kooomo", and Brother Koyomi's favourite colour is "o". Among all subsegments containing pieces of "o" only, "ooo" is the longest, with a length of 3. Thus the Koyomity of this garland equals 3.
But problem arises as Nadeko is unsure about Brother Koyomi's favourite colour, and has swaying ideas on the amount of work to do. She has q plans on this, each of which can be expressed as a pair of an integer mi and a lowercase letter ci, meanings of which are explained above. You are to find out the maximum Koyomity achievable after repainting the garland according to each plan.
The first line of input contains a positive integer n (1 ≤ n ≤ 1 500) — the length of the garland.
The second line contains n lowercase English letters s1s2... sn as a string — the initial colours of paper pieces on the garland.
The third line contains a positive integer q (1 ≤ q ≤ 200 000) — the number of plans Nadeko has.
The next q lines describe one plan each: the i-th among them contains an integer mi (1 ≤ mi ≤ n) — the maximum amount of pieces to repaint, followed by a space, then by a lowercase English letter ci — Koyomi's possible favourite colour.
Output q lines: for each work plan, output one line containing an integer — the largest Koyomity achievable after repainting the garland according to it.
6
koyomi
3
1 o
4 o
4 m
3
6
5
15
yamatonadeshiko
10
1 a
2 a
3 a
4 a
5 a
1 b
2 b
3 b
4 b
5 b
3
4
5
7
8
1
2
3
4
5
10
aaaaaaaaaa
2
10 b
10 z
10
10
In the first sample, there are three plans:
- In the first plan, at most 1 piece can be repainted. Repainting the "y" piece to become "o" results in "kooomi", whose Koyomity of 3is the best achievable;
- In the second plan, at most 4 pieces can be repainted, and "oooooo" results in a Koyomity of 6;
- In the third plan, at most 4 pieces can be repainted, and "mmmmmi" and "kmmmmm" both result in a Koyomity of 5.
显然一次询问可以O(n)完成
然而好像。。。m>=n的询问是没有意义的呀?
然后好像就只有26*1500种有效的询问,记忆化一下即可
1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define max(a,b) (a>b?a:b) 25 #define min(a,b) (a<b?a:b) 26 #define print_runtime printf("Running time:%.3lfs ",double(clock())/1000.0) 27 #define TO(j) printf(#j": %d ",j); 28 //#define OJ 29 using namespace std; 30 const int MAXINT = 100010; 31 const int MAXNODE = 100010; 32 const int MAXEDGE = 2*MAXNODE; 33 char BUF,*buf; 34 int read(){ 35 char c=getchar();int f=1,x=0; 36 while(!isdigit(c)){if(c=='-') f=-1;c=getchar();} 37 while(isdigit(c)){x=x*10+c-'0';c=getchar();} 38 return f*x; 39 } 40 char get_ch(){ 41 char c=getchar(); 42 while(!isalpha(c)) c=getchar(); 43 return c; 44 } 45 //------------------- Head Files ----------------------// 46 47 int s[1510],ans[26][1510],n; 48 void get_input(); 49 void work(); 50 int main() { 51 get_input(); 52 work(); 53 return 0; 54 } 55 void work(){ 56 memset(ans,-1,sizeof(ans)); 57 int q=read(),m,c; 58 while(q--){ 59 m=read();c=get_ch()-'a'; 60 if(m>=n) {printf("%d ",n);continue;} 61 if(ans[c][m]!=-1) {printf("%d ",ans[c][m]);continue;} 62 int cnt=0,l=0,t=0,i; 63 for(int i=0;i<n;i++){ 64 if(s[i]!=c) cnt++; 65 while(cnt>m) { 66 if(s[l]!=c) cnt--; 67 l++; 68 } 69 t=max(t,i-l+1); 70 } 71 printf("%d ",t); 72 ans[c][m]=t; 73 } 74 } 75 void get_input(){ 76 n=read(); 77 rep0(i,n) s[i] = getchar()-'a'; 78 }
The crowdedness of the discotheque would never stop our friends from having fun, but a bit more spaciousness won't hurt, will it?
The discotheque can be seen as an infinite xy-plane, in which there are a total of n dancers. Once someone starts moving around, they will move only inside their own movement range, which is a circular area Ci described by a center (xi, yi) and a radius ri. No two ranges' borders have more than one common point, that is for every pair (i, j) (1 ≤ i < j ≤ n) either ranges Ci and Cj are disjoint, or one of them is a subset of the other. Note that it's possible that two ranges' borders share a single common point, but no two dancers have exactly the same ranges.
Tsukihi, being one of them, defines the spaciousness to be the area covered by an odd number of movement ranges of dancers who are moving. An example is shown below, with shaded regions representing the spaciousness if everyone moves at the same time.
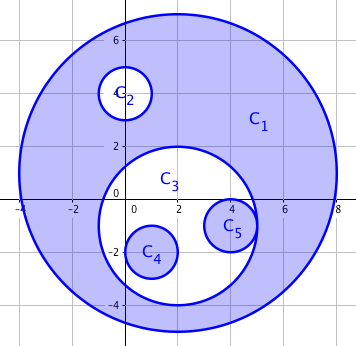
But no one keeps moving for the whole night after all, so the whole night's time is divided into two halves — before midnight and after midnight. Every dancer moves around in one half, while sitting down with friends in the other. The spaciousness of two halves are calculated separately and their sum should, of course, be as large as possible. The following figure shows an optimal solution to the example above.
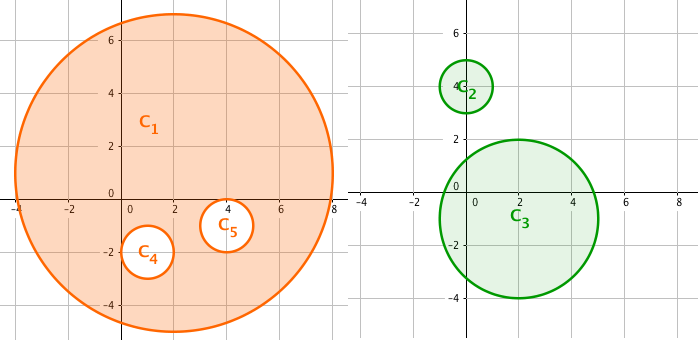
By different plans of who dances in the first half and who does in the other, different sums of spaciousness over two halves are achieved. You are to find the largest achievable value of this sum.
The first line of input contains a positive integer n (1 ≤ n ≤ 1 000) — the number of dancers.
The following n lines each describes a dancer: the i-th line among them contains three space-separated integers xi, yi and ri( - 106 ≤ xi, yi ≤ 106, 1 ≤ ri ≤ 106), describing a circular movement range centered at (xi, yi) with radius ri.
Output one decimal number — the largest achievable sum of spaciousness over two halves of the night.
The output is considered correct if it has a relative or absolute error of at most 10 - 9. Formally, let your answer be a, and the jury's answer be b. Your answer is considered correct if 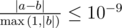 .
.
5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1
138.23007676
8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8
289.02652413
The first sample corresponds to the illustrations in the legend.
首先通过包含关系处理出一个树结构出来
然后这棵树上的每个节点可以有四种状态:上半夜正贡献,上半夜负贡献,下半夜正贡献,下半夜负贡献
不能有两个连续的上半夜正贡献或者下半夜正贡献
然后发现。。最优策略永远是树根选择上半夜,然后下面所有的点全部分配给下半夜

1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define max(a,b) (a>b?a:b) 25 #define min(a,b) (a<b?a:b) 26 #define print_runtime printf("Running time:%.3lfs ",double(clock())/1000.0) 27 #define TO(j) printf(#j": %d ",j); 28 //#define OJ 29 using namespace std; 30 const int MAXINT = 100010; 31 const int MAXNODE = 1010; 32 const int MAXEDGE = 2*MAXNODE; 33 const double PI = 3.14159265358979323846; 34 char BUF,*buf; 35 int read(){ 36 char c=getchar();int f=1,x=0; 37 while(!isdigit(c)){if(c=='-') f=-1;c=getchar();} 38 while(isdigit(c)){x=x*10+c-'0';c=getchar();} 39 return f*x; 40 } 41 char get_ch(){ 42 char c=getchar(); 43 while(!isalpha(c)) c=getchar(); 44 return c; 45 } 46 //------------------- Head Files ----------------------// 47 int cnt,n,fa[MAXNODE]; 48 struct circle{ 49 ll x,y,r; 50 circle(){} 51 circle(ll _x,ll _y,ll _r):x(_x),y(_y),r(_r){} 52 }c[MAXNODE]; 53 struct edge{ 54 int u,v; 55 edge *nxt; 56 edge(){} 57 edge (int _u,int _v,edge *_nxt):u(_u),v(_v),nxt(_nxt){} 58 }mp[MAXEDGE],*head[MAXNODE]; 59 void addedge(int u,int v){ 60 mp[cnt] = edge(u,v,head[u]); 61 head[u] = &mp[cnt++]; 62 mp[cnt] = edge (v,u,head[v]); 63 head[v] = &mp[cnt++]; 64 } 65 double dis(circle &a,circle &b){ 66 return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)); 67 } 68 int contain(circle &a,circle &b){ 69 return a.r>dis(a,b)+b.r-eps; 70 } 71 double dfs(int p,int cd){ 72 double s = c[p].r*c[p].r*PI; 73 if(cd>=1) s=-s; 74 iter(i,p){ 75 if(i->v==fa[p]) continue; 76 s+=dfs(i->v,(cd+1)%2); 77 } 78 return s; 79 } 80 void get_input(); 81 void work(); 82 int main() { 83 get_input(); 84 work(); 85 return 0; 86 } 87 void work(){ 88 double ans=0; 89 rep0(i,n){ 90 int f = -1; 91 rep0(j,n){ 92 if(i==j) continue; 93 if(contain(c[j],c[i])){ 94 if(f==-1||contain(c[f],c[j])) f=j; 95 } 96 } 97 fa[i]=f; 98 if(f!=-1) addedge(i,f); 99 } 100 rep0(i,n) if(fa[i]==-1) ans+=dfs(i,-1); 101 printf("%.10lf ",ans); 102 } 103 void get_input(){ 104 n=read(); 105 rep0(i,n){ 106 c[i].x=read();c[i].y=read();c[i].r=read(); 107 } 108 }
Those unwilling to return home from a long journey, will be affected by the oddity of the snail and lose their way. Mayoi, the oddity's carrier, wouldn't like this to happen, but there's nothing to do with this before a cure is figured out. For now, she would only like to know the enormous number of possibilities to be faced with if someone gets lost.
There are n towns in the region, numbered from 1 to n. The town numbered 1 is called the capital. The traffic network is formed by bidirectional roads connecting pairs of towns. No two roads connect the same pair of towns, and no road connects a town with itself. The time needed to travel through each of the roads is the same. Lost travelers will not be able to find out how the towns are connected, but the residents can help them by providing the following facts:
- Starting from each town other than the capital, the shortest path (i.e. the path passing through the minimum number of roads) to the capital exists, and is unique;
- Let li be the number of roads on the shortest path from town i to the capital, then li ≥ li - 1 holds for all 2 ≤ i ≤ n;
- For town i, the number of roads connected to it is denoted by di, which equals either 2 or 3.
You are to count the number of different ways in which the towns are connected, and give the answer modulo 109 + 7. Two ways of connecting towns are considered different if a pair (u, v) (1 ≤ u, v ≤ n) exists such there is a road between towns u and v in one of them but not in the other.
The first line of input contains a positive integer n (3 ≤ n ≤ 50) — the number of towns.
The second line contains n space-separated integers d1, d2, ..., dn (2 ≤ di ≤ 3) — the number of roads connected to towns 1, 2, ..., n, respectively. It is guaranteed that the sum of di over all i is even.
Output one integer — the total number of different possible ways in which the towns are connected, modulo 109 + 7.
4
3 2 3 2
1
5
2 3 3 2 2
2
5
2 2 2 2 2
2
20
2 2 2 2 3 2 3 2 2 2 2 2 2 2 2 2 2 3 3 2
82944
In the first example, the following structure is the only one to satisfy the constraints, the distances from towns 2, 3, 4 to the capital are all 1.
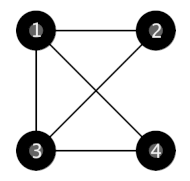
In the second example, the following two structures satisfy the constraints.
无桨不得行船,你的随身物品中有没有长直之物可以充当船桨一用?
莫慌,我有一******
什么破题
这个n=50也看不出复杂度,我晚上没写出来,第二天调了半天,发现是我第一天晚上写的一句话有问题,我忘了删掉,mmp
一个必须要看出的性质是一个点的距离是它所有连接的点的距离的最小值+1
我们先不考虑复杂度(因为看不出来),这显然是个dp计数题,先想想条件怎么用
1、最短路唯一:不知道有什么用,先放着
2、到点1的距离单调不降:这个给dp提供了划分阶段的方式,很重要
3、度数是2或者3:这个也不知道怎么用。。
那就先怼第二个条件,如果距离单调不降,说明什么?
说明我们在尝试给一个已经有n-1个点的图加入第n个点的时候,设n-1个点的图里离1号点最远的点距离为l,这个点只能连到距离为l-1的点或者距离为l的点上,不然他到1号点的距离就比l小了
这给我们提供了划分阶段的方式,现在我们尝试列出这样的一个状态表示:dp[i][j][k]表示有i个点的一张图,有j个点的距离是l-1,k个点的距离是l的方法数
这样好像不怎么能转移,因为我们不知道这些点还需要连出去多少边,不妨改成这样:dp[i][j][k]表示有i个点的一张图,有j条边需要连到距离为l-1的点,有k条边需要连到距离为l的点
这样看上去就可以转移了,但实际上还是有问题,因为我们不知道每个点有多少条边,这样会导致一个点的相同的两条边被计算两次,导致重复计数
这时候我们就需要用到第三个条件:把dp改成这样:dp[i][j1][j2][k1][k2]表示有i个点的一张图,有j1个点距离为l-1,需要连出1条边,j2个点距离为l-1,需要连出2条边,k1个点距离为l,需要练1条边,k2个点距离为l,需要连2条边
由于第二条性质,显然一个点必须和前面的点连一条边,所以它剩下的度数只能是1或者2,点1比较特殊需要单独考虑
这就可以不重不漏转移了,枚举下一个点和哪些点连边即可
转移巨烦
首先如果j1+j2==0,说明l-1的点不需要连出新边了,这时我们才能新建距离为l+1的点,否则在之后的图里永远无法满足l-1的点的连边需求
然后我们要分类讨论新加入点的度数
如果度数为2,允许的转移有:
连一个l-1
连一个l-1,一个l
如果都市为3,允许的转移有:
连一个l-1
连一个l-1,一个l
连一个l-1,两个l
还要讨论连的是k1还是k2,l1还是l2
注意底一条性质,所以我们不允许连两个l-1或者连两个l这种转移
然后时间复杂度是 n^5,注意到这样会炸空间(需要1.3个G),加一个滚动数组优化

1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define max(a,b) (a>b?a:b) 25 #define min(a,b) (a<b?a:b) 26 #define print_runtime printf("Running time:%.3lfs ",double(clock())/1000.0) 27 #define TO(j) printf(#j": %d ",j); 28 //#define OJ 29 using namespace std; 30 const int MAXINT = 100010; 31 const int MAXNODE = 100010; 32 const int MAXEDGE = 2 * MAXNODE; 33 char BUF, *buf; 34 int read() { 35 char c = getchar(); int f = 1, x = 0; 36 while (!isdigit(c)) { if (c == '-') f = -1; c = getchar(); } 37 while (isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); } 38 return f * x; 39 } 40 char get_ch() { 41 char c = getchar(); 42 while (!isalpha(c)) c = getchar(); 43 return c; 44 } 45 //------------------- Head Files ----------------------// 46 47 int dp[2][51][51][51][51]; // 48 int d[51], n; 49 void get_input(); 50 void work(); 51 void add(int &a, ll b) { 52 a = ((ll)(a) + b) % MOD; 53 } 54 int main() { 55 get_input(); 56 work(); 57 return 0; 58 } 59 void work() { 60 if (d[1] == 2 && d[2] == 2) dp[0][1][0][1][0] = 1; 61 if (d[1] == 3 && d[2] == 2) dp[0][0][1][1][0] = 1; 62 if (d[1] == 2 && d[2] == 3) dp[0][1][0][0][1] = 1; 63 if (d[1] == 3 && d[2] == 3) dp[0][0][1][0][1] = 1; 64 for (int i = 2; i < n; i++) { 65 int nx = !(i & 1); 66 memset(dp[nx], 0, sizeof(dp[nx])); 67 for (int j1 = 0; j1 < n; j1++) { //max-1 68 for (int j2 = 0; j2 < n; j2++) { 69 for (int k1 = 0; k1 < n; k1++) { // max 70 for (int k2 = 0; k2 < n; k2++) { 71 if (k1 + k2 + j1 + j2 > n) continue; 72 if (dp[i & 1][j1][j2][k1][k2] == 0) continue; 73 //if (k1 + k2 == 0) continue; 74 ll p = dp[i & 1][j1][j2][k1][k2]; 75 if (j1 + j2 == 0) { 76 if (d[i + 1] == 2) { 77 if (k1 != 0) add(dp[nx][k1 - 1][k2][1][0], p * k1); 78 if (k2 != 0) add(dp[nx][k1 + 1][k2 - 1][1][0], p * k2); 79 } 80 if (d[i + 1] == 3) { 81 if (k1 != 0) add(dp[nx][k1 - 1][k2][0][1], p * k1); 82 if (k2 != 0) add(dp[nx][k1 + 1][k2 - 1][0][1], p * k2); 83 } 84 } 85 if (d[i + 1] == 2) { 86 if (j1 != 0) { 87 add(dp[nx][j1 - 1][j2][k1 + 1][k2], p * j1); 88 if (k1 != 0) add(dp[nx][j1 - 1][j2][k1 - 1][k2], p * j1 * k1); 89 if (k2 != 0) add(dp[nx][j1 - 1][j2][k1 + 1][k2 - 1], p * j1 * k2); 90 } 91 if (j2 != 0) { 92 add(dp[nx][j1 + 1][j2 - 1][k1 + 1][k2], p * j2); 93 if (k1 != 0) add(dp[nx][j1 + 1][j2 - 1][k1 - 1][k2], p * j2 * k1); 94 if (k2 != 0) add(dp[nx][j1 + 1][j2 - 1][k1 + 1][k2 - 1], p * j2 * k2); 95 } 96 } 97 if (d[i + 1] == 3) { 98 if (j1 != 0) { 99 add(dp[nx][j1 - 1][j2][k1][k2 + 1], p * j1); 100 if (k1 != 0) add(dp[nx][j1 - 1][j2][k1][k2], p * j1 * k1); 101 if (k1 >= 2) add(dp[nx][j1 - 1][j2][k1 - 2][k2], p * j1 * k1 * (k1 - 1) / 2); 102 if (k2 != 0) add(dp[nx][j1 - 1][j2][k1 + 2][k2 - 1], p * j1 * k2); 103 if (k2 >= 2) add(dp[nx][j1 - 1][j2][k1 + 2][k2 - 2], p * j1 * k2 * (k2 - 1) / 2); 104 if (k1 != 0 && k2 != 0) add(dp[nx][j1 - 1][j2][k1][k2 - 1], p * j1 * k1 * k2); 105 } 106 if (j2 != 0) { 107 add(dp[nx][j1 + 1][j2 - 1][k1][k2 + 1], p * j2); 108 if (k1 != 0) add(dp[nx][j1 + 1][j2 - 1][k1][k2], p * j2 * k1); 109 if (k1 >= 2) add(dp[nx][j1 + 1][j2 - 1][k1 - 2][k2], p * j2 * k1 * (k1 - 1) / 2); 110 if (k2 != 0) add(dp[nx][j1 + 1][j2 - 1][k1 + 2][k2 - 1], p * j2 * k2); 111 if (k2 >= 2) add(dp[nx][j1 + 1][j2 - 1][k1 + 2][k2 - 2], p * j2 * k2 * (k2 - 1) / 2); 112 if (k1 != 0 && k2 != 0) add(dp[nx][j1 + 1][j2 - 1][k1][k2 - 1], p * j2 * k1 * k2); 113 } 114 } 115 } 116 } 117 } 118 } 119 } 120 printf("%d ", dp[n & 1][0][0][0][0]); 121 } 122 void get_input() { 123 n = read(); 124 rep1(i, n) d[i] = read(); 125 }
