Heidi's friend Jenny is asking Heidi to deliver an important letter to one of their common friends. Since Jenny is Irish, Heidi thinks that this might be a prank. More precisely, she suspects that the message she is asked to deliver states: "Send the fool further!", and upon reading it the recipient will ask Heidi to deliver the same message to yet another friend (that the recipient has in common with Heidi), and so on.
Heidi believes that her friends want to avoid awkward situations, so she will not be made to visit the same person (including Jenny) twice. She also knows how much it costs to travel between any two of her friends who know each other. She wants to know: what is the maximal amount of money she will waste on travel if it really is a prank?
Heidi's n friends are labeled 0 through n - 1, and their network of connections forms a tree. In other words, every two of her friends a, bknow each other, possibly indirectly (there is a sequence of friends starting from a and ending on b and such that each two consecutive friends in the sequence know each other directly), and there are exactly n - 1 pairs of friends who know each other directly.
Jenny is given the number 0.
The first line of the input contains the number of friends n (3 ≤ n ≤ 100). The next n - 1 lines each contain three space-separated integers u, v and c (0 ≤ u, v ≤ n - 1, 1 ≤ c ≤ 104), meaning that u and v are friends (know each other directly) and the cost for travelling between u and v is c.
It is guaranteed that the social network of the input forms a tree.
Output a single integer – the maximum sum of costs.
4
0 1 4
0 2 2
2 3 3
5
6
1 2 3
0 2 100
1 4 2
0 3 7
3 5 10
105
11
1 0 1664
2 0 881
3 2 4670
4 2 1555
5 1 1870
6 2 1265
7 2 288
8 7 2266
9 2 1536
10 6 3378
5551
In the second example, the worst-case scenario goes like this: Jenny sends Heidi to the friend labeled by number 2 (incurring a cost of 100), then friend 2 sends her to friend 1 (costing Heidi 3), and finally friend 1 relays her to friend 4 (incurring an additional cost of 2).
这三个题的意思不是很接近，我就分开来上题面了，这是Eazy
大概意思是求树上的一条链使得边权和最大，签到题，一遍DFS
代码我用了下面一题的k=1版本
Thank you for helping Heidi! It is now the second of April, but she has been summoned by Jenny again. The pranks do not seem to end...
In the meantime, Heidi has decided that she does not trust her friends anymore. Not too much, anyway. Her relative lack of trust is manifested as follows: whereas previously she would not be made to visit the same person twice, now she can only be sure that she will not be made to visit the same person more than k times. (In the case of Jenny, this includes her first visit in the beginning. The situation from the easy version corresponds to setting k = 1.)
This is not as bad as it looks, since a single ticket for a route between two friends allows Heidi to travel between this pair of friends the whole day (in both directions). In other words, once she pays for travel between a pair of friends, all further travels between that pair are free.
How much money will Heidi waste now, in a worst-case scenario?
The first line contains two space-separated integers – the number of friends n (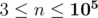
) and the parameter k (1 ≤ k ≤ 105). The next n - 1 lines each contain three space-separated integers u, v and c (0 ≤ u, v ≤ n - 1, 1 ≤ c ≤ 104) meaning that u and v are friends and the cost for traveling between u and v is c.
It is again guaranteed that the social network of the input forms a tree.
Again, output a single integer – the maximum sum of costs of tickets.
9 3
0 1 1
0 2 1
1 3 2
1 4 2
1 5 2
2 6 3
2 7 3
2 8 3
15
9 5
0 1 1
0 2 1
1 3 2
1 4 2
1 5 2
2 6 3
2 7 3
2 8 3
17
11 6
1 0 7932
2 1 1952
3 2 2227
4 0 9112
5 4 6067
6 0 6786
7 6 3883
8 4 7137
9 1 2796
10 5 6200
54092
In the first example, the worst-case scenario for Heidi is to visit the friends in the following order: 0, 1, 5, 1, 3, 1, 0, 2, 6, 2, 7, 2, 8. Observe that no friend is visited more than 3 times.
这是Medium
求树上的边权最大的复杂路径，每个点允许经过K次，一条边多次经过算一次权值
树形dp
首先权在边上不方便，把每个边的权值分配给它底下的点
每个点维护两个值：
1、从这个点下去再上来能获得的最大值 up
2、从这个点下去然后不上来获得的最大值 noup
怎么求这个东西呢
对于叶子节点肯定这两个就是节点的权值
首先一个点如果要下去再上来，那从它最多能访问它的k-1个儿子，且这些儿子都要下去再上来，把他所有儿子拿出来排个序取前k-1个即可
然后是不上来，显然除了刚才取到的下去再上来的k-1个儿子，还可以额外选一个儿子下去不上来，这个需要一些技巧，直接选不好办，我们考虑差分
选择一个本来就选的儿子的收益是
这个点的noup-这个点的up+第k大的儿子的up
选择一个本来没有选的儿子的收益是这个点的noup
在所有儿子的收益里取一个最大值即可
最终答案是0号点的noup
1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define print_runtime printf("Running time:%.3lfs ",double(clock())/1000.0) 25 #define TO(j) printf(#j": %d ",j); 26 //#define OJ 27 using namespace std; 28 const int MAXINT = 100010; 29 const int MAXNODE = 100010; 30 const int MAXEDGE = 2 * MAXNODE; 31 char BUF, *buf; 32 int read() { 33 char c = getchar(); int f = 1, x = 0; 34 while (!isdigit(c)) {if (c == '-') f = -1; c = getchar();} 35 while (isdigit(c)) {x = x * 10 + c - '0'; c = getchar();} 36 return f * x; 37 } 38 char get_ch() { 39 char c = getchar(); 40 while (!isalpha(c)) c = getchar(); 41 return c; 42 } 43 //------------------- Head Files ----------------------// 44 int n, k, cnt,val[MAXNODE]; 45 struct info{ 46 ll up,noup; 47 info(int _u,int _n):up(_u),noup(_n){} 48 info(){} 49 }dp[MAXNODE],tmp[MAXNODE]; 50 bool operator < (const info &a,const info &b){ 51 return a.up>b.up; 52 } 53 struct edge { 54 int u, v, l; 55 edge *nxt; 56 edge() {} 57 edge(int _u, int _v, int _l, edge *_nxt): u(_u), v(_v), l(_l), nxt(_nxt) {} 58 } mp[MAXEDGE], *head[MAXNODE]; 59 void addedge(int u, int v, int l) { 60 mp[cnt] = edge(u, v, l, head[u]); 61 head[u] = &mp[cnt++]; 62 mp[cnt] = edge(v, u, l, head[v]); 63 head[v] = &mp[cnt++]; 64 } 65 void dfs(int p,int fa){ 66 int cnt_s=0,up=val[p],noup=val[p],b; 67 vector<info> tmp; 68 ll add=0; 69 iter(i,p){ 70 if(i->v==fa) continue; 71 val[i->v]=i->l; 72 dfs(i->v,p); 73 cnt_s++; 74 tmp.push_back(dp[i->v]); 75 } 76 b=min(k-1,cnt_s); 77 sort(tmp.begin(),tmp.end()); 78 rep0(i,b) up+=tmp[i].up; 79 rep0(i,cnt_s) { 80 if(i<b) { 81 if(b<cnt_s) add=max(add,tmp[i].noup-tmp[i].up+tmp[b].up); 82 else add=max(add,tmp[i].noup-tmp[i].up); 83 }else{ 84 add=max(add,tmp[i].noup); 85 } 86 } 87 dp[p].up=up; 88 dp[p].noup=up+add; 89 } 90 void get_input(); 91 void work(); 92 int main() { 93 get_input(); 94 work(); 95 return 0; 96 } 97 void work() { 98 dfs(0,-1); 99 printf("%lld ",dp[0].noup); 100 } 101 void get_input() { 102 n=read();k=read(); 103 rep0(i,n-1){ 104 int u=read(),v=read(),l=read(); 105 addedge(u,v,l); 106 } 107 }
Heidi is terrified by your estimate and she found it unrealistic that her friends would collaborate to drive her into debt. She expects that, actually, each person will just pick a random friend to send Heidi to. (This randomness assumption implies, however, that she can now visit the same friend an arbitrary number of times...) Moreover, if a person only has one friend in common with Heidi (i.e., if that person is in a leaf of the tree), then that person will not send Heidi back (so that Heidi's travel will end at some point).
Heidi also found unrealistic the assumption that she can make all the travels in one day. Therefore now she assumes that every time she travels a route between two friends, she needs to buy a new ticket. She wants to know: how much should she expect to spend on the trips?
For what it's worth, Heidi knows that Jenny has at least two friends.
The first line contains the number of friends n (3 ≤ n ≤ 105). The next n - 1 lines each contain three space-separated integers u, v and c (0 ≤ u, v ≤ n - 1, 1 ≤ c ≤ 104) meaning that u and v are friends and the cost for traveling between u and v is c (paid every time!).
It is again guaranteed that the social network of the input forms a tree.
Assume that the expected cost of the trips is written as an irreducible fraction a / b (that is, a and b are coprime). Then Heidi, the weird cow that she is, asks you to output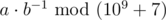 
. (Output a single integer between 0 and 109 + 6.)
3
0 1 10
0 2 20
15
4
0 1 3
0 2 9
0 3 27
13
7
0 1 3
0 5 7
1 2 2
1 3 1
1 4 5
5 6 8
400000019
11
1 0 6646
2 0 8816
3 2 9375
4 2 5950
5 1 8702
6 2 2657
7 2 885
8 7 2660
9 2 5369
10 6 3798
153869806
6
0 1 8
0 2 24
1 3 40
1 4 16
4 5 8
39
In the first example, with probability 1 / 2 Heidi will go to 1 from 0, and with probability 1 / 2 she will go to 2. In the first case the cost would be 10, and in the second it would be 20. After reaching 1 or 2 she will stop, as 1 and 2 are leaves of the social tree. Hence, the expected cost she has to pay is 10·1 / 2 + 20·1 / 2 = 15.
In the third example, the expected cost is 81 / 5. You should output 400000019.
In her travels, Heidi has learned an intriguing fact about the structure of her social network. She tells you the following: The mysterious determinant that you might be wondering about is such that it does not cause strange errors in your reasonable solution... Did we mention that Heidi is a weird cow?
题目大意：叶子节点为终止节点，每个点等概率选一条边走，求1号点走到终止节点的期望距离
最后这个保证真迷。。翻译一下是：如果你的算法正确，你可能在考虑的那个神秘的行列式不会导致奇怪的问题
我知道是高斯消元啊！然而n^3怎么做啊（摔
又是一道神题，看了题解才写出来
假设e[u]表示从u开始走到终止节点的期望，d[u]表示u的度数，l表示边长
考虑一下需要高斯消元的方程，它大概长这样对吧
$ e[u] = frac{1}{d[u]} sum_{v}{(e[v]+l_{u,v})} $
这个东西直接做自然是n^3的，但是你考虑一下叶子节点的方程，它是这样的
$ e[u] = 0 $
然后呢？然后我们把所有e[u]消掉（事实上只有他的父亲节点才有e[u]项），并把这个点从图上删去，重复这一行为直到我们删掉了所有的初始的叶子，现在我们有一些新的叶子，它们的方程是这样的
$ e[u] = frac{1}{d[u]} e[fa] + c $
我们可以继续消，最终叶子节点方程的一般形式是这样的
$ k*e[u] = frac{1}{d[u]} e[fa] + b $
这个形式保证了每一次消元是O(log1e9+7)的，总共需要消元n-1次，总复杂度O(nlog1e9+7)
事实上我们只要对每个点存储k和b就行了
1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define print_runtime printf("Running time:%.3lfs ",double(clock())/1000.0) 25 #define TO(j) printf(#j": %d ",j); 26 //#define OJ 27 using namespace std; 28 const int MAXINT = 100010; 29 const int MAXNODE = 100010; 30 const int MAXEDGE = 2 * MAXNODE; 31 char BUF, *buf; 32 int read() { 33 char c = getchar(); int f = 1, x = 0; 34 while (!isdigit(c)) {if (c == '-') f = -1; c = getchar();} 35 while (isdigit(c)) {x = x * 10 + c - '0'; c = getchar();} 36 return f * x; 37 } 38 char get_ch() { 39 char c = getchar(); 40 while (!isalpha(c)) c = getchar(); 41 return c; 42 } 43 //------------------- Head Files ----------------------// 44 int n, cnt, d[MAXNODE]; 45 struct info{ 46 ll k,b; 47 info(int _k,int _b):k(_k),b(_b){} 48 info(){} 49 }dp[MAXNODE],tmp[MAXNODE]; 50 ll rev(ll b){ 51 ll ans = 1,u=MOD-2; 52 for(;u;b=b*b%MOD,u>>=1) if(u&1) ans=ans*b%MOD; 53 return ans; 54 } 55 struct edge { 56 int u, v, l; 57 edge *nxt; 58 edge() {} 59 edge(int _u, int _v, int _l, edge *_nxt): u(_u), v(_v), l(_l), nxt(_nxt) {} 60 } mp[MAXEDGE], *head[MAXNODE]; 61 void addedge(int u, int v, int l) { 62 mp[cnt] = edge(u, v, l, head[u]); 63 head[u] = &mp[cnt++]; 64 mp[cnt] = edge(v, u, l, head[v]); 65 head[v] = &mp[cnt++]; 66 } 67 void dfs(int p,int fa){ 68 ll _d; 69 if(d[p]==1) _d=0; else _d=rev(d[p]); 70 dp[p].k=1; 71 iter(i,p) dp[p].b+=_d*i->l; 72 dp[p].b%=MOD; 73 74 iter(i,p){ 75 if(i->v==fa) continue; 76 dfs(i->v,p); 77 } 78 if(p==0) return ; 79 if(d[p]!=1){ 80 ll _fd = rev(d[fa]); 81 ll k = rev(dp[p].k); 82 dp[fa].b=(dp[fa].b+_fd*(dp[p].b*k%MOD))%MOD; 83 dp[fa].k=((dp[fa].k-_fd*(_d*k%MOD))%MOD+MOD)%MOD; 84 } 85 } 86 void get_input(); 87 void work(); 88 int main() { 89 get_input(); 90 work(); 91 return 0; 92 } 93 void work() { 94 dfs(0,-1); 95 printf("%lld ",dp[0].b*rev(dp[0].k)%MOD); 96 } 97 void get_input() { 98 n=read(); 99 rep0(i,n-1){ 100 int u=read(),v=read(),l=read(); 101 addedge(u,v,l); 102 d[u]++;d[v]++; 103 } 104 }