题目描述

输入输出格式
输入格式:

输出格式:
对于每个询问操作,输出一行答案。
输入输出样例
输入样例#1:
6 5 2 2 1 2 1 1 1 2 1 3 2 4 2 5 2 6 Q 3 5 C 2 1 1 Q 3 5 C 5 1 2 Q 3 5
输出样例#1:
3 1 2
说明
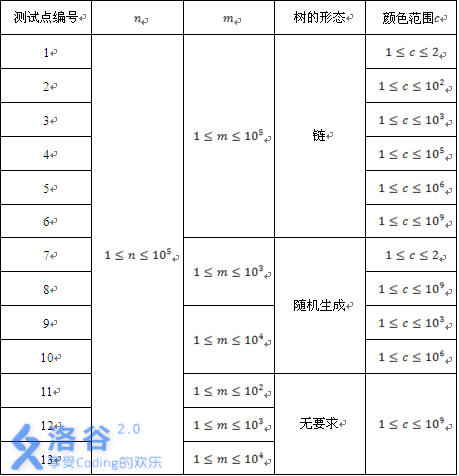

题目大意:给一棵树,要求支持链覆盖+查询链上颜色段数
先考虑链上怎么做吧,颜色段数这个东西支持区间加,一个区间可以用三个属性表示:左端点的颜色,右端点的颜色,区间颜色段数
两段合并以后的颜色段数是:左段颜色段数+右段颜色段数-(左段右端点颜色==右段左端点颜色)
然后既然链上可以线段树,那树上直接树链剖分就好了
注意一下这个区间加是不满足交换律的,要交换的话需要取反,树剖查询到最后的时候要分类讨论一下
1 #include <iostream> 2 #include <cstdlib> 3 #include <cstdio> 4 #include <algorithm> 5 #include <string> 6 #include <cstring> 7 #include <cmath> 8 #include <map> 9 #include <stack> 10 #include <set> 11 #include <vector> 12 #include <queue> 13 #include <time.h> 14 #define eps 1e-7 15 #define INF 0x3f3f3f3f 16 #define MOD 1000000007 17 #define rep0(j,n) for(int j=0;j<n;++j) 18 #define rep1(j,n) for(int j=1;j<=n;++j) 19 #define pb push_back 20 #define set0(n) memset(n,0,sizeof(n)) 21 #define ll long long 22 #define ull unsigned long long 23 #define iter(i,v) for(edge *i=head[v];i;i=i->nxt) 24 #define max(a,b) (a>b?a:b) 25 #define min(a,b) (a<b?a:b) 26 #define print_runtime printf("Running time:%.3lfs ",double(clock())/1000.0) 27 #define TO(j) printf(#j": %d ",j); 28 //#define OJ 29 using namespace std; 30 const int MAXINT = 100010; 31 const int MAXNODE = 100010; 32 const int MAXEDGE = 2 * MAXNODE; 33 char BUF, *buf; 34 int read() { 35 char c = getchar(); int f = 1, x = 0; 36 while (!isdigit(c)) { if (c == '-') f = -1; c = getchar(); } 37 while (isdigit(c)) { x = x * 10 + c - '0'; c = getchar(); } 38 return f * x; 39 } 40 char get_ch() { 41 char c = getchar(); 42 while (!isalpha(c)) c = getchar(); 43 return c; 44 } 45 //------------------- Head Files ----------------------// 46 int c[MAXINT],cl[MAXINT]; 47 struct node { 48 int lb, rb; 49 node *l, *r; 50 int num, lc, rc, tag; 51 void color(int c) { 52 num = 1; 53 lc = rc = tag = c; 54 } 55 void pushdown() { 56 if (tag) { 57 l->color(tag); r->color(tag); 58 tag = 0; 59 } 60 } 61 void pushup() { 62 lc = l->lc; rc = r->rc; 63 num = l->num + r->num - (l->rc == r->lc); 64 } 65 node() { 66 lb = rb = num = lc = rc = tag = 0; 67 } 68 }; 69 struct seg { 70 int lc, rc, num; 71 seg() {} 72 seg(int _lc, int _rc, int _num) : lc(_lc), rc(_rc), num(_num) {} 73 }; 74 seg add(seg a, seg b) { 75 if (a.lc == -1) return b; 76 if (b.lc == -1) return a; 77 seg ans; 78 ans.lc = a.lc; 79 ans.rc = b.rc; 80 ans.num = a.num + b.num - (a.rc == b.lc); 81 return ans; 82 } 83 struct SegTree { 84 node mp[MAXINT * 4]; 85 node *root; 86 int _cnt; 87 SegTree() { 88 _cnt = 0; 89 } 90 node *newnode(int l, int r) { 91 node *p = &mp[_cnt++]; 92 p->lb = l; 93 p->rb = r; 94 return p; 95 } 96 void maketree(int lb, int rb, node *&p) { 97 p = newnode(lb, rb); 98 if (rb - lb > 1) { 99 maketree(lb, (lb + rb) / 2, p->l); 100 maketree((lb + rb) / 2, rb, p->r); 101 p->pushup(); 102 } 103 else { 104 p->lc = p->rc = c[lb]; 105 p->num = 1; 106 } 107 } 108 void cover(int lb, int rb, int c, node *p) { 109 if (lb >= p->rb || rb <= p->lb) return; 110 if (lb <= p->lb && rb >= p->rb) { p->color(c); return; } 111 p->pushdown(); 112 cover(lb, rb, c, p->l); 113 cover(lb, rb, c, p->r); 114 p->pushup(); 115 } 116 seg query(int lb, int rb, node *p) { 117 if (lb >= p->rb || rb <= p->lb) return seg(-1, -1, -1); 118 if (lb <= p->lb && rb >= p->rb) return seg(p->lc, p->rc, p->num); 119 p->pushdown(); 120 return add(query(lb, rb, p->l), query(lb, rb, p->r)); 121 } 122 } st; 123 int n, m, fa[MAXINT], sz[MAXINT], top[MAXINT], dfn[MAXINT], cnt_dfn = 1, dep[MAXINT], cnt; 124 struct edge { 125 int u, v; 126 edge *nxt; 127 edge() {} 128 edge(int _u, int _v, edge *_nxt) : u(_u), v(_v), nxt(_nxt) {} 129 } mp[MAXINT * 2], *head[MAXINT]; 130 void addedge(int u, int v) { 131 mp[cnt] = edge(u, v, head[u]); 132 head[u] = &mp[cnt++]; 133 mp[cnt] = edge(v, u, head[v]); 134 head[v] = &mp[cnt++]; 135 } 136 void dfs1(int p) { 137 sz[p] = 1; 138 iter(i, p) { 139 if (i->v == fa[p])continue; 140 fa[i->v] = p; dep[i->v] = dep[p] + 1; 141 dfs1(i->v); 142 sz[p] += sz[i->v]; 143 } 144 } 145 void dfs2(int p) { 146 int mx = 0, gs = 0; 147 dfn[p] = cnt_dfn++; 148 iter(i, p) { 149 if (i->v == fa[p]) continue; 150 if (sz[i->v] > mx) { 151 mx = sz[i->v]; 152 gs = i->v; 153 } 154 } 155 if (gs == 0) return; 156 top[gs] = top[p]; 157 dfs2(gs); 158 iter(i, p) { 159 if (i->v == fa[p] || i->v == gs) continue; 160 top[i->v] = i->v; 161 dfs2(i->v); 162 } 163 } 164 seg trans(seg a) { 165 return seg(a.rc, a.lc, a.num); 166 } 167 void modify(int l, int r, int c) { 168 while (top[l] != top[r]) { 169 if (dep[top[l]] > dep[top[r]]) { 170 st.cover(dfn[top[l]], dfn[l]+1, c, st.root); 171 l = fa[top[l]]; 172 } 173 else { 174 st.cover(dfn[top[r]], dfn[r]+1, c, st.root); 175 r = fa[top[r]]; 176 } 177 } 178 st.cover(min(dfn[r], dfn[l]), max(dfn[r], dfn[l])+1, c, st.root); 179 } 180 int query(int l, int r) { 181 seg ansl(-1, -1, -1), ansr(-1, -1, -1); 182 while (top[l] != top[r]) { 183 if (dep[top[l]] > dep[top[r]]) { 184 ansl = add(st.query(dfn[top[l]], dfn[l]+1, st.root), ansl); 185 l = fa[top[l]]; 186 } 187 else { 188 ansr = add(st.query(dfn[top[r]], dfn[r]+1, st.root), ansr); 189 r = fa[top[r]]; 190 } 191 } 192 if (dep[l] > dep[r]) { 193 ansl = add(trans(ansr), add(st.query(dfn[r], dfn[l]+1, st.root), ansl)); 194 } 195 else { 196 ansl = add(trans(ansl), add(st.query(dfn[l], dfn[r]+1, st.root), ansr)); 197 } 198 return ansl.num; 199 } 200 void get_input(); 201 void work(); 202 int main() { 203 get_input(); 204 work(); 205 return 0; 206 } 207 void work() { 208 dfs1(1); 209 dfs2(1); 210 rep1(i, n) c[dfn[i]] = cl[i]; 211 st.maketree(1, n + 1, st.root); 212 while (m--) { 213 char op = get_ch(); 214 int u, v, c; 215 if (op == 'C') { 216 u = read(), v = read(), c = read(); 217 modify(u, v, c); 218 } 219 else { 220 u = read(); v = read(); 221 printf("%d ", query(u, v)); 222 } 223 } 224 } 225 void get_input() { 226 n = read(); m = read(); 227 rep1(i, n) cl[i] = read(); 228 rep0(i, n - 1) { 229 int u = read(), v = read(); 230 addedge(u, v); 231 } 232 }