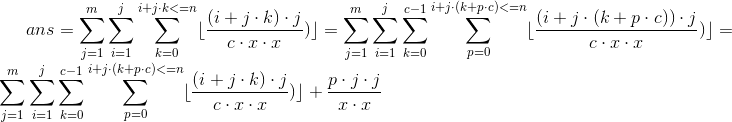HDU5970 最大公约数
Describe
有这样一个有关最大公约数的函数:
函数 f(x, y):
{
c=0
当 y>0:
{
c +=1
t = x % y
x = y
y = t
}
返回 c * x * x
}
给出三个正整数n,m,p,你需要计算: (sum_{i=1}^{n}sum_{j=1}^{m} lfloor frac{i*j}{f(i,j)} floor) 对p取模的结果。
Input
包含多组测试数据。
第一行有一个正整数,表示数据的组数。
接下来每行表示一组数据,这一行有三个空格隔开的正整数n,m,p。
保证 n <= 666,666,666, m <= 666, p <= 666,666,666。
最终的测试数据中共有66组数据,并且每一个n,m,p都是在上述范围内均匀随机生成的。
Output
对于每个输入数据输出一行,这一行只包含一个整数即答案。
Sample Input
3
10 5 23333
100 10 23333
1000 20 23333
Sample Output
271
22359
10998
Solution
f(x,y)可以分析出是(gcd(x,y)^2)*c,c是x,y辗转相除的次数。
所以我们可以知道,f(x,y)中的x和y顺序可换结果一样,还知道只要如果gcd()相等且第一次运算x%y相等(辗转相除的次数相等),f()就相等。
即:f ( i , j ) = f ( j , i );
f ( i , j ) = f(i + j * k, j );
所以有一个推导过程 (sum_{i=1}^{n}sum_{j=1}^{m} lfloor frac{i*j}{f(i,j)}
floor) =