加油加油, 与 \(\text{Part2}\) 的结束无缝衔接了/ybyb .
\(\text{【PER \#1】平均分}\)
\(\color{green}{\text{[EASY]}}\)
合理, 我永远做不出 \(brute\;force\) 题.
考虑 \(meeting\;in\;mddle\) , \(\mathcal{O}(3^{\lceil\frac{n}{2}\rceil})\) 爆搜出两侧的组.
对于一个三元组 \((x,y,z)\) 我们可以将左边的映射成 \((x-y,y-z)\) , 右边的映射成 \((y-x,z-y)\) , 考虑合并左右的二元组 \((a_1,b_1),(a_2,b_2)\) , 不妨设 \(x\leqslant y \leqslant z\) , 所以合并条件为 \(a_1\leqslant a_2,b_1\leqslant b_2\) , 我们需最小化 \(a_1+b_1-a_2-b_2\) .
剩下的双指针, 和一个类似二维数点的问题, 排序后树状数组即可.
时间复杂度 \(3^{\lceil\frac{n}{2}\rceil}n\) .
\(\text{【PER \#1】括号序列}\)
\(\color{green}{\text{[EASY]}}\)
很套路啊, 看到范围就知道要容斥了.
考虑容斥, 设 \(f_i\) 表示有序地选择 \(i\) 个位置的有序对, 使得每对的下标之差均为 \(M\) 的倍数的方案数, 然后选择 \(i\) 个括号放进这些位置, 其它 \(2N-2i\) 个随便放, 所以答案即为 \(\sum\limits_{i=0}^{N}{(-1)^i(2N-2i)!\binom{N}{i}f_i}\) .
而计算 \(f_i\) 也是很简单啊, 对于下标差为 \(M\) 的倍数, 我们可以分为 \(M\) 个等价类, 考虑每个等价类有多少个, \(f_i=[\frac{z^i}{i!}]\prod\limits_{j=0}^{M-1}{\sum\limits_{k=0}^{\lfloor\frac{n_j}{2}\rfloor}{\frac{n_j!}{(n_j-2k)!}\frac{z^k}{k!}}}\) , 其中 \(n_j\) 表示 \([1,2N]\) 中模 \(M\) 的余数为 \(j\) 的数的个数.
暴力计算多项式乘法可过, 时间复杂度 \(\mathcal{O}(n^2)\) , \(NTT\) 优化复杂度 \(\mathcal{O}(n\log{n})\) .
\(\text{【UR \#19】清扫银河}\)
\(\color{red}{\text{[HARD]}}\)
了解一下环路空间和断路空间是件好事, 以下只在连通图上做说明.
环路是一个边集, 满足它所对应的子图的点集的度数均为偶数, 并且形成回路, 可以看成一个欧拉回路.
环路空间是个线性空间, 满足里面的环路线性无关, 是个线性基. 环路满足两个环路做对称差运算之后还是环路.
简单证明一下, 考虑两个环路的交点, 先不删去重复路径, 交点的度数奇偶性不变, 因为重复的路径恰好被覆盖两次, 所以删去之后奇偶性仍不变, 对于没有相交的部分奇偶性不变.
再在此基础上考虑操作一, 一个生成树的非树边对应一个环路, 而这 \(m-n+1\) 个环路形成的环路空间即为一组线性基, 所以在所有节点度数均为偶数的图均在环路空间内, 因此一定可以通过至多 \(m-n+1\) 次操作使所有边合法.
因此我们的目标是把整张图的点的度数变为偶数, 引出断路空间的概念.
断路也是一个边集, 其定义与割集类似, 但并不要求极小, 且允许空集, 具体的, 断路为无向图割去断路中的边之后, 整张图可以被分为两个点集, 点集之间的点互不连通, 由此定义可知有孤点的时候断路可以为空集.
断路空间是一个线性空间, 满足里面的断路线性无关, 是个线性基, 断路满足两个断路做对称差运算之后还是断路.
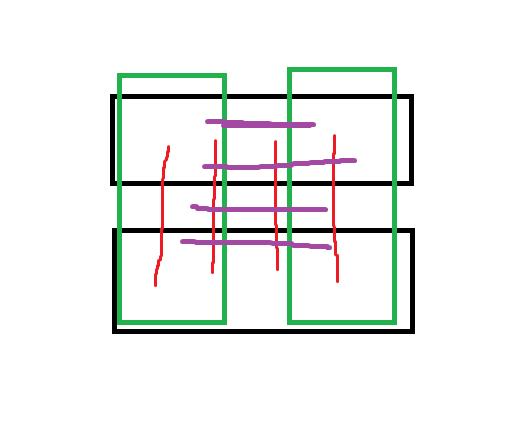
给出理解方式, 即断路的对称差长什么样, 并非证明.
其中我们令上面的黑色方框为 \(s_1\) , 下面的黑色方框为 \(t_1\) 表示一个断路分成的两个子图, 其中红色为其断路, 左边的绿色方框为 \(s_2\) , 右边的为 \(t_2\) 表示另一个断路分成的两个子图, 紫色为其断路.
我们令 \(s_1\) 和 \(s_2\) 的交与 \(t_1\) 和 \(t_2\) 的交为 \(s_3\) , \(s_2\) 与 \(t_1\) 的交与 \(s_1\) 和 \(t_2\) 的交为 \(t_3\) , 表示其对称差形成的断路分成的两个子图.
回到原题, 操作二实际上就是操作一个断路, 而操作多次断路其实是可以合并成一个的, 所以操作二只会进行 \(1\) 次.
于是总操作次数为 \(m-n+2\ll m+1\) , 至此我们完全丢弃了操作次数限制, 只用判断是否可变为全 \(0\) 的图.
考虑操作二断路空间的大小, 对于一个生成树, 断掉一条树边与最少的非树边使其不连通, 这是一条断路, 不难发现每条树边对应的断路可以构成一个线性基, 所以断路空间大小为 \(n-1\) .
我们按给出的图暴力建出线性基, 并判断每条边, 至此我们得到了一个 \(\mathcal{O}(\dfrac{m^3}{\omega})\) 的算法, 稍微优化可到 \(\mathcal{O}(\dfrac{nm^2}{\omega})\) .
现在考虑优化这个做法, 考虑边是没前途的了, 发现我们只在乎是否能把图变成所有点的度数均为偶数的图.
那么可以把操作二变形一下, 操作一个集合 \(S\) 将其中的点变为白点, 其余变黑进行翻转, 等价于依次对集合 \(S\) 中的每个点操作, 单独将其变成白点, 其余为黑点, 进行一次翻转操作.
考虑用 \(0/1\) 异或方程描述这么一件事, 设 \(f_i\) 表示是否操作了点 \(i\) , \(d_i\) 表示点 \(i\) 的度数, \(p_i\) 表示初始状态下点 \(i\) 连接的 \(1\) 边数量的奇偶性, 那么有异或方程,
其中求和符号不是相加是异或, 若次方程有解则原图有解.
时间复杂度 \(\mathcal{O}(\dfrac{n^3}{\omega})\) .
\(\text{【UR \#19】通用测评号}\)
\(\color{red}{\text{[HARD]}}\)
转化题意, 认为每个仓容量无限, 每次随机选择一个仓加 \(1\) , 问在所有仓大于等于 \(b\) 时大于等于 \(a\) 的仓的期望数量, 这是因为不关注操作具体数量.
根据期望的线性性, 考虑仓 \(1\) 的燃料大于等于 \(a\) 时, 存在仓小于等于 \(b\) 的概率, 每个仓一样, 乘 \(n\) 即为答案.
考虑容斥, 钦定 \(p\) 个仓燃料小于 \(b\) , 此时我们只关心这 \(p+1\) 个仓, 可以忽略其它仓, 再次转化问题, 初始给出一个序列 \(S\) , 每次在 \([1,p+1]\) 的整数中均匀随机一个数放入序列 \(S\) 末尾, 计算当序列中有 \(a\) 个 \(1\) 时, \(2\sim p+1\) 的出现次数均小于 \(b\) 的概率, 答案即等于,
后面部分是每个位置的贡献, 前面是多重排列.
由于只有 \(\sum{x_i}\) 和 \(\prod{x_i}\) 不同, 设 \(F(x)=\sum\limits_{i=0}^{b-1}{\frac{x^i}{i!}}\) , \(G(x)=F(x)^p\) , 那么答案即为,
考虑如何快一点求出 \(G(x)\) , 非卷积的多项式运算可以考虑求导, \(F'=F-\frac{x^{b-1}}{(b-1)!}\) , 那么 \((F^i)'=iF^i-iF^{i-1}\frac{x^{b-1}}{(b-1)!}\) , 算出后面的部分可以直接对比系数计算.
时间复杂度 \(\mathcal{O}(n^3)\) .
\(\text{【UR \#19】前进四}\)
\(\color{blue}{\text{[NORMAL]}}\)
先考虑一个暴力做法, 从后往前扫一遍, 维护后缀 \(\min\) 与答案, 考虑优化, 从后往前扫, 维护每个时刻从序列末扫到当前位置的信息, 维护两个值, 后缀 \(\min\) , 和一个时刻后缀 \(\min\) 被更新了多少次.
一个修改对应时间轴上的一个区间, 使用吉老师线段树, 时间复杂度 \(\mathcal{O}(n\log{n})\) .
\(\text{【LOJ\#3830】「IOI2022」鲶鱼塘}\)
\(\color{green}{\text{[EASY]}}\)
注意到连续的堤是单峰形的, 并且间隔开的只能是 \(a_i=n\) 或者 \(a_i=0\) , 那么可以直接 \(dp\) , 设 \(dp_{i,0/1}\) 表示重新编号为 \(i\) 的鱼, 当前列是在构造下降 / 上升, 的最大重量, 转移考虑转移到同一列还是下一列.
时间复杂度 \(\mathcal{O}(n\log{n})\) .
\(\text{【PNOR\#1\;div1】波特分组}\)
\(\color{green}{\text{[EASY]}}\)
考虑一种分组的概率, 设最后一个分到 \(A\) 的编号为 \(i_A\) , 最后一个分到 \(B\) 的概率为 \(i_B\) , 则概率为 \(2^{-\min\{i_A,i_B\}}\) .
枚举 \(\min\{i_A,i_B\} = p\) , 计算分组方案数, 分 \(p=b_k,b_i<p<b_{i+1},p>b_k\) , 其方案数分别为 \(\binom{b_k-k}{n-k},\binom{p-i-1}{n-1},\binom{p-k-1}{n-k-1}\) .
因为本质不同的 \(k\) 只有 \(\sqrt{S}\) 个, 所以复杂度为 \(\mathcal{O}(n\sqrt{S}+S)\) .
\(\text{【LOJ\#2831】「JOISC 2018 Day 1」道路建设}\)
\(\color{green}{\text{[EASY]}}\)
相当于求链上逆序对数, \(LCT\) 加树状数组维护即可, 时间复杂度 \(\mathcal{O}(n\log^2{n})\) .
\(\text{【LOJ\#2833】「JOISC 2018 Day 1」帐篷}\)
\(\color{green}{\text{[EASY]}}\)
考虑暴力的平方 \(dp\) , 设 \(f_{i,j}\) 表示 \(i\times j\) 的矩阵的答案.
由于加一行或一列没有本质区别, 只考虑加一列, 新一列什么也不放, \(f_{i,j}\leftarrow f_{i,j-1}\) , 新一列放在一个没放帐篷的行 \(f_{i,j}\leftarrow 4\times i\times f_{i-1,j-1}\) , 新一列放两个帐篷 \(f_{i,j}\leftarrow \binom{i}{2}f_{i-2,j-1}\) , 新一列放一个, 并和之前的一个匹配 \(f_{i,j}\leftarrow i\times (j-1)\times f_{i-1,j-2}\) .
最后还有减去啥都不放的情况.
时间复杂度 \(\mathcal{O}(n^2)\) .
\(\text{【PNOP\#2 div1】恰钱}\)
\(\color{green}{\text{[EASY]}}\)
不一定正确, 但能过.
暴力跑一跑发现, 两个相邻的好数间隔最多不超过 \(5\times 10^4\) , 事实上超过 \(4\times 10^4\) 的也只有 \(11\) 个, 超过 \(10^4\) 也很少, 所以可能确实卡不掉.
离线左端点排序跑暴力即可.
土豆, 土豆, 土豆好吃, 好土豆.