3171. 【GDOI2013模拟4】重心

Description

给你N个长2高h的矩形的质量 \(m_i\)，这 N 个矩形被放置在笛卡尔坐标系中：

1. 矩形的四条边平行于坐标轴；
2. 每个矩形下面的水平边的y坐标值互不相同，分别是0,h,2h,3h,...,(N-1)h；
3. 最下面的矩形的左下角坐标为(-2,0)，即右下角在原点处。

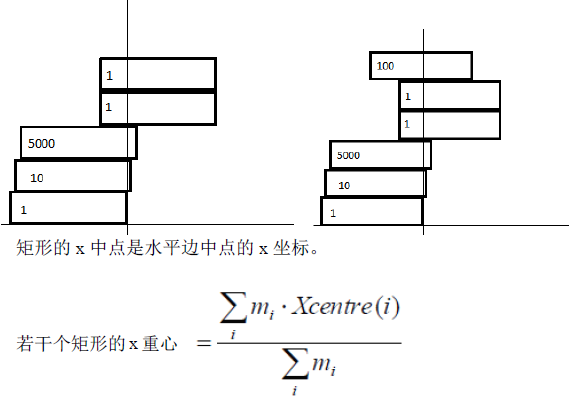
一种矩形的摆放方式是稳定的，当且仅当满足：每个矩形上面的所有矩形的 \(x\) 重心跟该矩形的 \(x\) 中点相距不超过1。上面左图是不稳定的而右图是稳定的。

给你N个矩形的质量，要求在不改变矩形的上下顺序的前提下找到一种稳定的摆放方式，同时输出所有稳定摆放方式中最右边矩形右下角 \(x\) 坐标的最大值。

Solution

先上结论，当我们从上往下做的时候，对于第 \(i\) 个块，他对重心的移动量为 \(\dfrac{m_i}{\sum m}\)。

考虑证明，考虑当前为第 \(i\) 个块，设 \(i+1\sim n\) 的块的重心为 0，那么加入第 \(i\) 个块后的重心为 \(\dfrac{\sum_{j=i}^na_j\times m_j}{\sum m}=\dfrac{0+a_i\times m_i}{\sum m}\)，而 \(a_i\) 不是 1 就是 -1，所以加入第 \(i\) 个块后对于重心的改变量为 \(\dfrac{m_i}{\sum m}\)。

Code

#include<cstdio>
#include<algorithm>
#define N 300005
#define db double
using namespace std;
int n,s,a[N];
db ans;
int read()
{
    int res=0;char ch=getchar();
    while (ch<'0'||ch>'9') ch=getchar();
    while (ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch-'0'),ch=getchar();
    return res;
}
int main()
{
    n=read();
    for (int i=1;i<=n;++i)
        a[i]=read();
    for (int i=n;i>1;--i)
    {
        s+=a[i];
        db x=db(a[i])/db(s);
        ans=max(ans,max(ans+x,2-x));
    }
    printf("%.6lf",ans);
    return 0;
}