Description
( ext{xyx}) 喜欢双射。
他惊奇的发现, 对于所有长度为 (n) 的排列,交换每个排列在区间 ([l,r]) 中的最小值和最大值,得到的排列两两不同,这构成了一个双射!
他很喜欢这个操作,于是他又掏出了两个排列 (left{a_{n} ight},left{b_{n} ight}),他希望用不超过 (m) 次操作来把 (left{a_{n} ight}) 变成 (left{b_{n} ight})。
Solution
首先发现操作可逆,因此可以将题目转换成 ({a_n} ightarrow 1dots n ightarrow {b_n})。而这两步是一样的,所以到此为止,这题的目的就是利用题目给出的操作来给一个序列排序。
再想到一个基本操作:reverse 一个有序区间,代价是 (frac{len}{2})。具体步骤是操作 ({l,r},{l+1,r-1}dots,{mid,mid+1})。
直接排序没有什么好的思路,可以用分治。
分治到区间 ([l,r]),尝试跟归并类似的操作,先让 ([l,mid]) 和 ([mid+1,r]) 有序,然后在合并两个区间。
假设此时是这个样子:
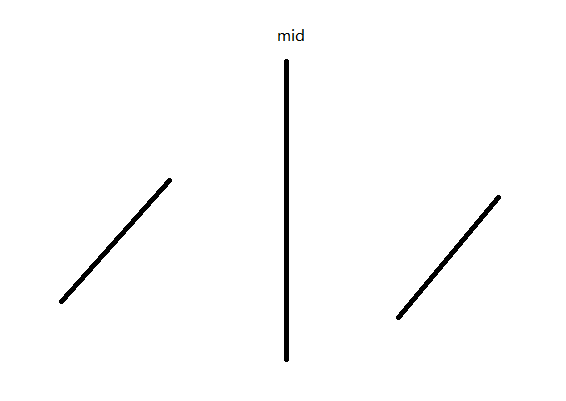
考虑将 ([l,mid]) 中 (le a[frac{r-l+1}{2}]) 的部分放在左边,(> a[frac{r-l+1}{2}]) 的部分放在右边,可以跟归并类似的使用双指针。
在 ([l,mid]) 内找出应该放在右边的那一部分,也在 ([mid+1,r]) 内找出应该放在左边的那一部分。
例如下图:

将这两个部分翻转,变成这样:
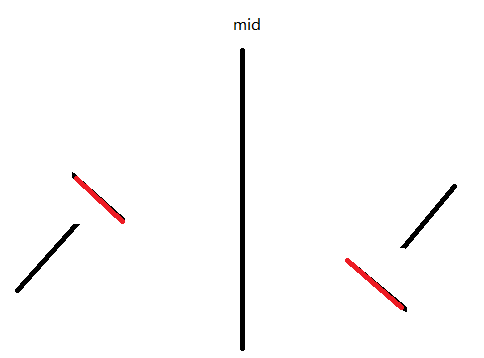
然后将两个红色的部分整体翻转,就成了这样:

这时我们的目的也就达成了,接下来就是继续向下分治了。
注意一个细节,就是将 (b_i) 求答案的时候,最后要讲操作反着输,因为是逆操作。
Code
#include<cstdio>
#include<algorithm>
#define N 4005
#define M 300005
using namespace std;
int n,m,res,ans1,ans2,a[N],ans[M][3];
void rever(int l,int r)
{
for (int x=l,y=r;x<y;++x,--y)
{
ans[++res][1]=x;ans[res][2]=y;
swap(a[x],a[y]);
}
}
void Sort(int l,int r,int mid)
{
if (l>=r) return;
int x=l-1,y=mid;
while (x-l+1+y-mid<(r-l+1)>>1)
if (y==r||(x<mid&&a[x+1]<a[y+1])) ++x;
else ++y;
rever(x+1,mid);rever(mid+1,y);
rever(x+1,y);
mid=l+(x-l+1)+(y-mid)-1;
Sort(l,mid,x);Sort(mid+1,r,y);
}
void solve(int l,int r)
{
if (l>=r) return;
int mid=(l+r)>>1;
solve(l,mid);solve(mid+1,r);
Sort(l,r,mid);
}
int main()
{
freopen("trans.in","r",stdin);
freopen("trans.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;++i)
scanf("%d",&a[i]);
solve(1,n);
for (int i=1;i<=n;++i)
scanf("%d",&a[i]);
ans1=res;
solve(1,n);
ans2=res;
for (int i=ans1+1,j=ans2;i<=j;++i,--j)
swap(ans[i],ans[j]);
printf("%d
",ans2);
for (int i=1;i<=ans2;++i)
printf("%d %d
",ans[i][1],ans[i][2]);
return 0;
}