博客作业04--树

1.学习总结

1.1树结构思维导图

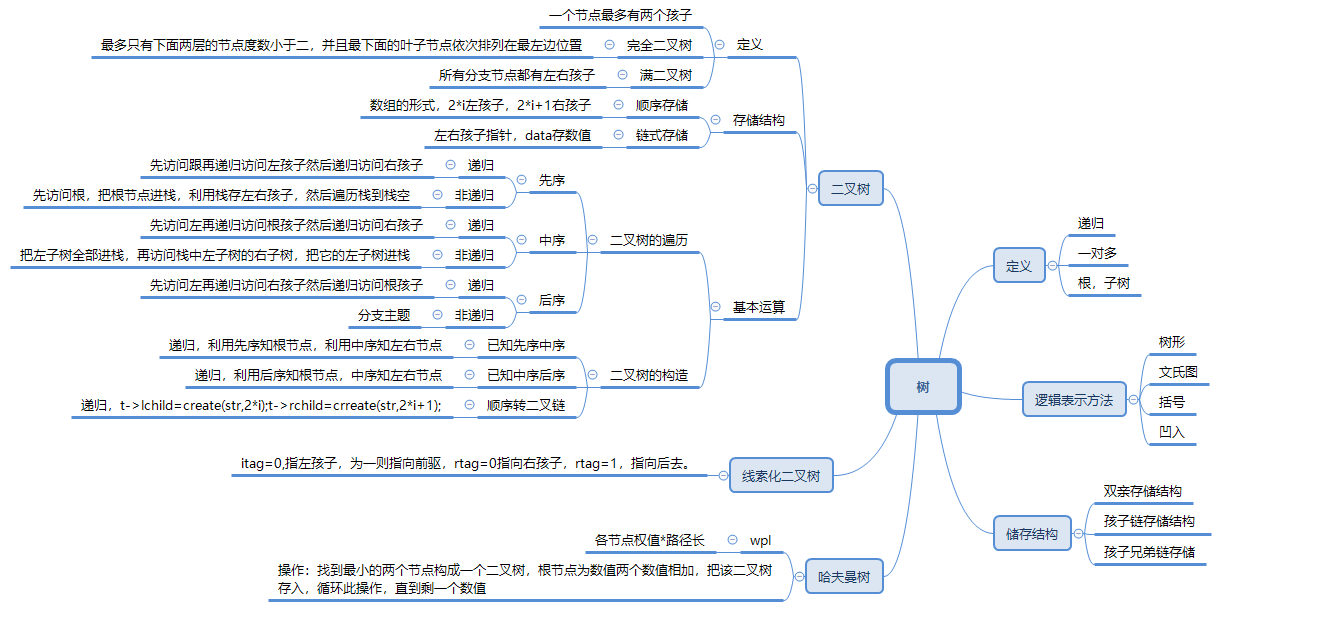
1.2 树结构学习体会

• 树的综合难度较大，需要使用到之前的知识，比如在建树时会用到栈的知识。
• 需要记住很多基础代码才能顺利的做题，如建二叉树哈夫曼树之类的代码，凭自己写很难也很浪费时间。

2.PTA实验作业

2.1 题目1：题目名称6-4 jmu-ds-表达式树

2.2 设计思路（伪代码或流程图）

void InitExpTree(BTree &T,string str)
{
	遍历字符串str{
		如果当前字符串为数字{
			T->data=当前数字 
			入栈Q1 
		 } 
		 如果当前字符串为运算符{
		 	与Q2栈顶比较优先级
			 优先级低入栈Q2
			 优先级相同Q2出栈
			 优先级高 T->data=Q2栈顶元素 
		 } 
	} 
}
double EvaluateExTree(BTree T)
{
	double x,y;
	x=递归调用左子树的值
	y=递归调用右子树的值
	根据data的运算符分别运算并返回结果 
}

2.3 代码截图

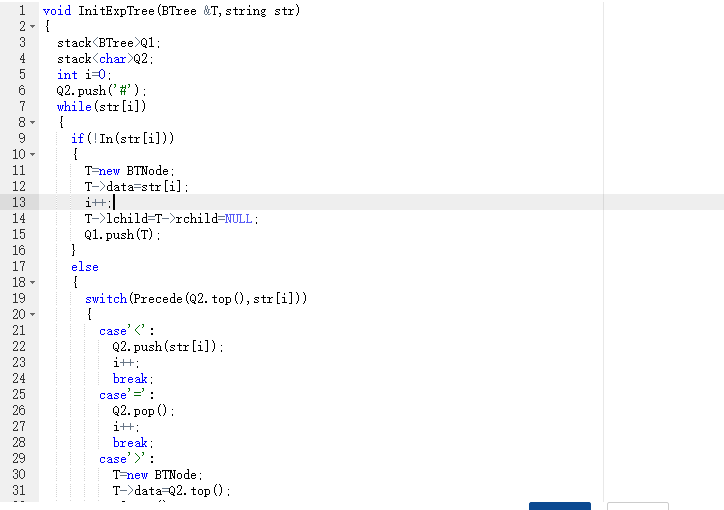
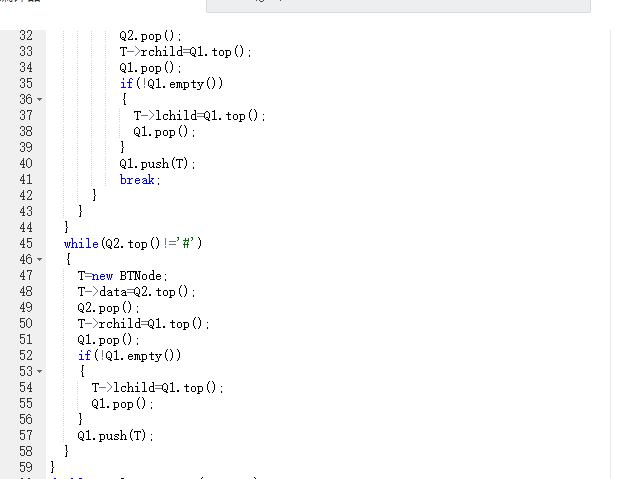
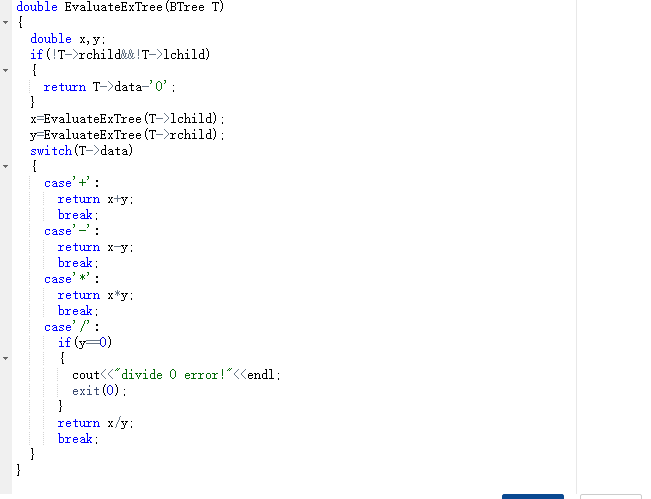
2.4 PTA提交列表说明。

2.1 题目2：6-2 求二叉树高度

2.2 设计思路（伪代码或流程图）

int GetHeight( BinTree BT )
{
	递归调用求高度函数 求出左子树高度
	递归调用求高度函数 求出右子树高度 
		return求出最高加1 
	
}

2.3 代码截图

2.4 PTA提交列表说明。

2.1 题目3：7-1 还原二叉树

2.2 设计思路（伪代码或流程图）

int main(){
	输入节点数N
	a字符数组存先序 b字符数组存中序 
	建树
	输出length 
} 
int length(BTNode *node){
	l=递归算出左子数最大高度 
	r=递归算出右子数最大高度 
	if(l>=r) return l+1;
	else return r+1;
}

2.3 代码截图

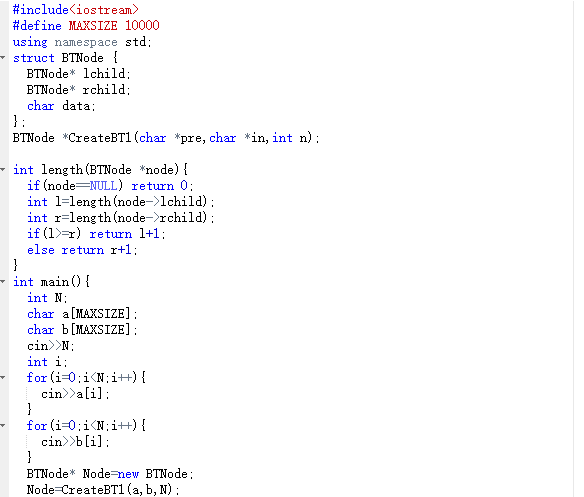
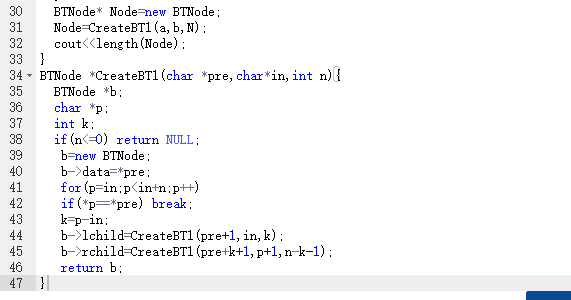
2.4 PTA提交列表说明。

3.截图本周题目集的PTA最后排名

3.1 PTA排名

3.2 我的得分：130

4. 阅读代码

• 功能：求树的宽度

• 地址：https://blog.csdn.net/K346K346/article/details/51076268