杭电多校第四场 E Matrix from Arrays

Problem E. Matrix from Arrays

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 474    Accepted Submission(s): 202

Problem Description

Kazari has an array A length of L, she plans to generate an infinite matrix M using A.
The procedure is given below in C/C++:

int cursor = 0;

for (int i = 0; ; ++i) {
    for (int j = 0; j <= i; ++j) { 
        M[j][i - j] = A[cursor];
        cursor = (cursor + 1) % L;
    }
}

Her friends don't believe that she has the ability to generate such a huge matrix, so they come up with a lot of queries about M, each of which focus the sum over some sub matrix. Kazari hates to spend time on these boring queries. She asks you, an excellent coder, to help her solve these queries.

 

Input

The first line of the input contains an integer T (1≤T≤100) denoting the number of test cases.
Each test case starts with an integer L (1≤L≤10) denoting the length of A.
The second line contains L integers A0,A1,...,AL−1 (1≤Ai≤100).
The third line contains an integer Q (1≤Q≤100) denoting the number of queries.
Each of next Q lines consists of four integers x0,y0,x1,y1 (0≤x0≤x1≤108,0≤y0≤y1≤108) querying the sum over the sub matrix whose upper-leftmost cell is (x0,y0) and lower-rightest cell is (x1,y1).

 

Output

For each test case, print an integer representing the sum over the specific sub matrix for each query.

 

Sample Input

1

3

1 10 100

5

3 3 3 3

2 3 3 3

2 3 5 8

5 1 10 10

9 99 999 1000

 

Sample Output

1

101

1068

2238

33076541

 

题意：先输入一个a数组，然后按题目给的构造方法构造出一个矩阵，然后我们输入一个区间，输出区间子矩阵和

思路：因为他的范围特别大，矩阵大小有10^8*10^8，说明我们肯定不能构造出子矩阵，既然不能全部构造出来，然后我们再看题目所给的构造方法

大了之后就取模往前，可能有规律，我们就构造出100*100的矩阵，看是否有规律

我们可以发现它是有矩阵周期的，把偶数和奇数的情况都打一遍，发现奇数的时候是以n为一个周期，偶数是2*n

那既然后面的都是相同的，那么我们就没必要构造出来，a数组最大长度是10，所以我们循环矩阵最大是20*20，我们只要把

循环矩阵计算出来即可，后面的相同的不再重复计算，当我们输入一个区间的时候，我们只要算边界和里面循环矩阵的个数即可

这里我们再用到一个二维前缀和来优化我们的时间

b[i][j]  代表i行j列的矩阵的和

二维前缀和这里就不再讲述，我说下怎么由我们的循环矩阵的前缀和延伸到总的大矩阵的前缀和

我们要计算 x y的矩阵前缀和，我们只知道循环矩阵，那我们现在来计算

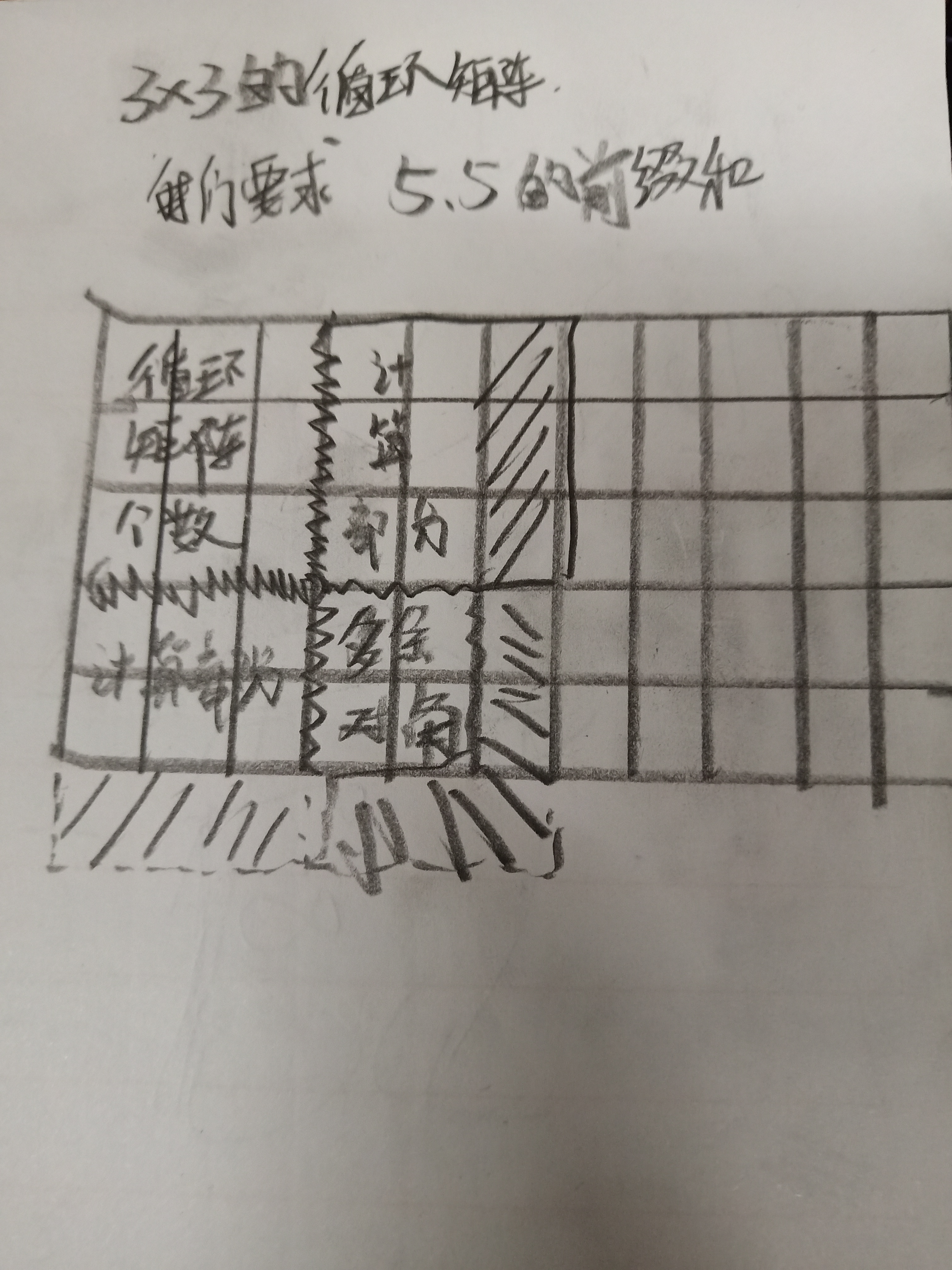
‘我们3*3的循环矩阵，我们要求5*5的前缀和

我们首先计算出里面包括了多少个循环矩阵

 b[n-1][n-1]*(x/n)*(y/n)

b[n-1][n-1]是我们的循环矩阵和，（x/n）代表我的行区间有多少个，（y/n）代表列区间有多少个，乘起来就是总共的了

然后我们计算循环矩阵后，我们要来计算多余的边界
但是他是循环矩阵，所以我们只要进行取模n就能把坐标映射到循环矩阵上
所以行和列都是同理，都还要分别乘以(x/n)和（y/n）
而我们还剩下一个对角，对角可以直接计算，不用除，
看下图

详细解释看代码

#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
ll a[11];
ll b[50][50];
int n,m;
ll cal(int x,int y)
{
    if(x<0||y<0) return 0;
    return b[n-1][n-1]*(x/n)*(y/n)+b[x%n][n-1]*(y/n)+b[n-1][y%n]*(x/n)+b[x%n][y%n];//计算循环矩阵的个数  列的多余边界 　行的多余边界   对角的多余边界   
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {    
        scanf("%d",&n);
        for(int i=0;i<n;i++)
        scanf("%lld",&a[i]);
        int cursor = 0;
        for (int i = 0; i<=45; ++i) {//填充我们的矩阵
            for (int j = 0; j <= i; ++j) { 
                b[j][i - j] = a[cursor];
                cursor = (cursor + 1) % n;
            }
        }
        n=2*n;
        for(int i=0;i<n;i++)//计算循环矩阵的二维前缀和
        {
            for(int j=0;j<n;j++)
            {
                if(i) b[i][j]+=b[i-1][j];
                if(j) b[i][j]+=b[i][j-1];
                if(i&&j) b[i][j]-=b[i-1][j-1];
            }
        }
        int x1,x2,y1,y2;
        scanf("%d",&m);
        while(m--)
        {
            scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
            printf("%lld
",cal(x2,y2)-cal(x2,y1-1)-cal(x1-1,y2)+cal(x1-1,y1-1));//二维前缀和的计算方法（用前缀大矩阵分别减去行列矩阵，但是行列中间重复了一个小矩阵，需要再加上）
        }
    }
}