xj4604 排序

(n,k <= 1e5).
先考虑二分出这个值,check 有多少段的平均值小于这个 mid,这个在之前的复活赛中是原题 T4,数形结合,$ ext{Average} = frac{Sum_i-Sum_j}{i-j} $,可以把它看做一个两点间的斜率公式——每个位置把它搞到平面上的点对 ((i,Sum_i)),求有多少点对的斜率小于 mid。把它分成每个点的贡献——分别求一个点左侧有多少点能与它斜率小于等于 mid,过每个点作一条斜率为 mid 的直线,求出纵截距 (-mid imes i + Sum_i),这就是一个二维偏序问题了,用归并排序就行。
考虑怎么优化掉一个 (log)——不妨把每个点的这个截距式看做以 (mid)为变量的函数,可以得到这样的东西——
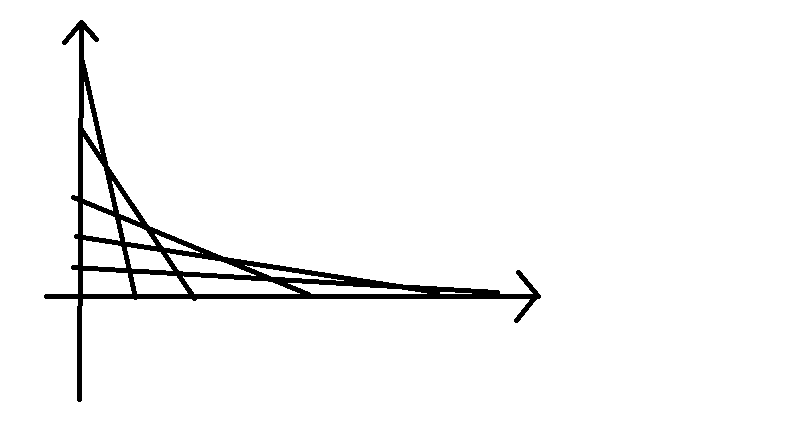
上面的每一个交点都代表一个区间的平均值,求横坐标第 k 大的交点—— k 不是很大,所以就可以这么求:从左到右扫,假设我们知道线段在当前横坐标、的按照纵坐标的排序的结果,那么下一个交点肯定由相邻的两条线段得到;然后我们再扫到下一个交点的横坐标,显然只有这两条线段的上下关系发生变化,交换一下就可以得出下一个序列......差不多就是这个意思,代码见 Peanut_Tang 学长的 代码。
xj4591 program

(n,a,b <= 3e2).
直接上状态:设 $f[i][j][k] $表示现在在枚举第 i 行字符串、枚举到了第 j 个位置、当前连续段长度为 k 的最小代价,于是可以得到转移方程:
上面的方程是四次方的,下面的是三次方的,只要优化上面的就行了。展开之后用上斜率优化就行了。有的时候,状态的设置要清楚明确一点,分情况来写,就非常有利于分析。
xj4592 birthday

巧妙的构造题(数竞内鬼题)。
我们构造如下:

可以通过巧妙的递归来实现:
int f[maxn][maxn][maxn];
void dfs(int x, int y, int z, int dep)
{
if (z <= 0) return;
if (f[dep][x][y]) return;
f[dep][x][y] = z;
dfs(x - 1, y, z - 1, dep + 1);
dfs(x, y - 1, z - 2, dep + 1);
dfs(x, y + 1, z - 3, dep + 1);
dfs(x + 1, y, z - 4, dep + 1);
}
int main()
{
//vector<oper> v;
int n;
cin >> n;
dfs(105, 105, n, 1);
for (int i = 200; i; i--)
{
for (int j = 200; j; j--)
{
for (int k = 200; k; k--)
{
if (f[i][j][k])
{
cout << j << " " << k << " " << f[i][j][k] << endl;
}
}
}
}
return 0;
}
华灵「蝶妄想」 (butterfly)

又是一道构造题,有一个东西我们是知道的——若我们把第一行选上了,那么必然会破坏掉 (frac{1}{2}m) 列。同理,最后一行、最后一列、第一列都不值得选上——若我们能构造出方案数与(n)、(m)呈系数为一的方法,那么当(n leq 4)时肯定是必须这么做更优——于是我们可以得到一个答案为 (n+m-4) 的构造:
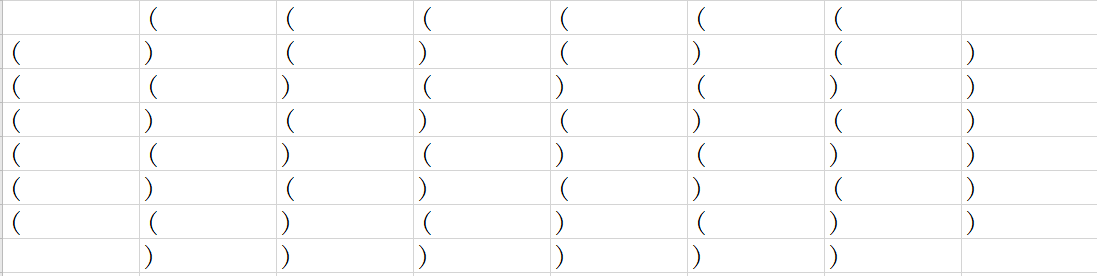
当(n)足够大时,这个是最优的,但是(n=2)和(n=4)要特判。
樱符「完全墨染的樱花」 (sakura)

(n<=1e5,m<=5e5).
显然这张图是一个仙人掌,先来考虑树的情况怎么做。
大胆的运用最大流最小割定理,两点之间的最大流就等于它们路径上的最小值。这个东西最难优化的地方在于求最小值,所以我们把边权从小到大依次加入,新加入的这条边就是它联通的两个连通块之间的点对的最大流的值。于是我们用并查集统计这一过程的贡献;具体来说,维护每个连通块的(p^c)之和与(p^{c(n-1)})之和,每次合并的时候加上这条边的贡献就行了。
然后考虑仙人掌怎么做。由于环没有重叠,我们分成一个个环来讨论:可以发现把每个环上的最小的边去掉,并把它的容量加到这个环的其他边上,这个新的树的最小割和原来的最小割完全等价,在这棵树上按照原来的方法统计就行了,用树上差分更新权值就能保证复杂度。
正确性的证明:显然。
xj4584 随机游走
你从 A 出发,接下来的每一天,你会从 x 达到 (x+f(x))modM,问 N−1 天后你的位置,其中 f(x) 表示 x 十进制表示中最大的数码。
(n<=1e6)直接暴力、(m<=1e6)开个桶找循环节,这都简单。考虑怎么优化。
这是一道求值的题目,又推不出什么式子,所以只能考虑倍增。我们先把它增大到$
咕着咕着
幽曲「埋骨于弘川」 (buried)
跟上一题做法类似,也咕着吧。
燃烧的火焰 (flame)

(Theta(n2^klog n))做法就比较显然,枚举k中每个点选还是不选,以这个点集为起点,跑一遍最短路就行了,看一下最短路最远的那个点的距离是否比原答案大。
事实上我们发现我们根本不用跑这么多次的最短路,我们只需要跑 (k)次最短路就可以了。形式化的,若当前枚举到的子集是(T),则点(x)的最短路就是(max_{iin T}{dis_{i,x}})。那我们要求的,就是
的子集T的个数。我们直接处理这个 (k) 显然过于困难。由于每个点的对答案的限制是分别独立的,所以单独看一下一个点的贡献:出发点们到它的距离有些小于答案,有些大于答案;当且仅当选出的出发点全部属于这个距离大于答案的点集时,它会不合法。所以我们开一个(2^k)的桶,每次把这个集合和它的子集全部删掉。如何快速删除子集呢?考虑离线下来一起处理。从大到小扫描桶的值域,当扫到一个删掉的集合时,枚举去掉它的哪一位,把这(k)个集合设为非法;否则 ans++。
这么做显然是不重不漏的,巧妙的不得了。
消失的序列 (stack)
喵喵喵啊!lzy: 对于栈的计数问题,有一种常见的数形结合方法:

图中,向右的一条边代表了一次入栈,向上的一条边代表了一次出栈;由于入栈和出栈序列已经定下来了,所以每条边的边权就已经定下来了,如图所示;一条从((0,0))到((n,n))路径对应了一种入栈和出栈的方式;我们要统计(a)数组的个数,其实每个(a)数组与((0,0))到((n,n))的路径也一一对应,因为根据出栈序列和路径可以还原出唯一且存在的入栈序列。现在考虑加上这个(a_{pos}=x)的限制,如图:
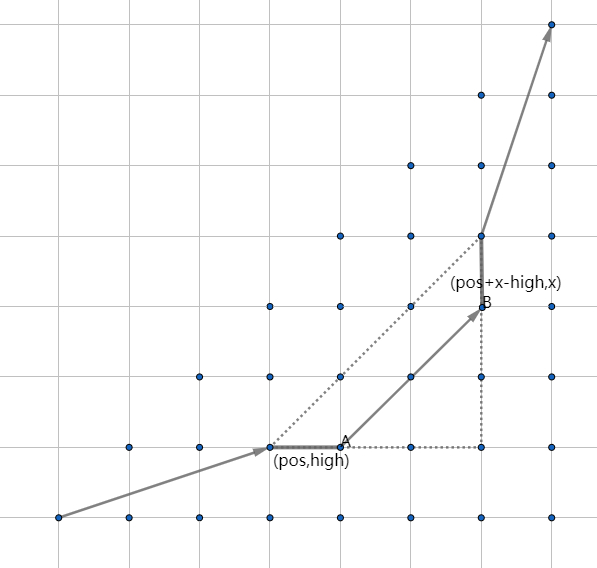
枚举(pos)位置的高度,由于出栈的限制,我们可以得出它必定经过上边的那个出栈序列;现在问题就转化为从((0,0))到((pos,high))再到那个再到((n,n))的方案数的乘积。这个方案数怎么求呢?
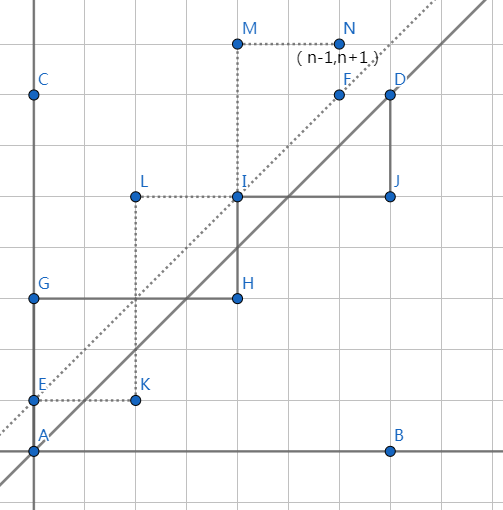
用总的方案数(C_{2n}^n)减去不合法的方案数。发现不合法的方案一定会经过(y=x+1)那条线,若把这些方案沿(y=x+1)翻转,于是它最后会到达点((n-1,n+1));我们大胆猜想:不合法的方案与从((0,0))到((n-1,n+1))的方案数一一对应,合法的方案数就是(C_n=C_{2n}^n-C_{2n}^{n-1})。类似的,若三角形是((n,m)),那么不合法就是从((0,0))走到((m-1,n+1)),合法方案数就是(C_{n,m}=C_{n+m}^n-C_{n+m}^{n+1}),这个叫类卡特兰数。
另外,许多问题(如节点数是(n)的二叉树个数)可以通过(O(n^2))的递推式$C_n=sum_{j=0}^{n-1} C_j C_{n-j-1} $ 来证明答案是卡特兰数。具体右转 lzy 大佬的 Blog。