Problem List(其实这几场全是附中出的)
这场比赛的题目相当有价值,特别是前两题,相当的巧妙。
A.路径二进制
数据范围这么小,当然是搜索。
(30pts:)大力搜索出奇迹,最后统计答案的时候拿一个桶存一下已经统计了哪些数,由于(d<=20),所以(result<=2^20),所以还是存的下的。
(60pts:)我们发现重复状态其实非常之多,我们加上一个记忆化进行剪枝:(vis[i][t][S])表示(i)号点、时间是(t)、当前数是(S)是否已经访问过,如果已经访问过那就可以回溯了。时间复杂度和空间复杂度都是(O(nd2^d))的,时间上可以过满数据,但是空间会被卡。
(100pts:)相当巧妙的方法来优化空间:我们在搜索时进行折半,只从一开始搜索长度为(frac{1}{2}d)的链并用状压存下是否可达存下来,然后分别在每个点往外搜索长度为(frac{1}{2}d)的链并状压存下,最后遍历每个点暴力合并前后两段就可以了。空间复杂度是(n^22^{frac{1}{2}d}+2^d)的,时间是(n^22^d)的。
B.停车场
(20pts:)悬线法可以解决静态的平面最大全0矩阵问题。当然也可以用(DP)解决:设(f_{i,j})为在结点((i,j))向左上能延伸的最大方形的边长,(h_{i,j})为向上能有多少个空位,(r_{i,j})是向左的空位,于是得到(f_{i,j}=min{r_{i,j},h_{i,j},f_{i-1,j-1}+1$。复杂度)O(n^2m)$。
(70pts:)你会发现没有这一档部分分,这个是我考场上乱搞搞出来的分数。你会发现一个神奇的性质:
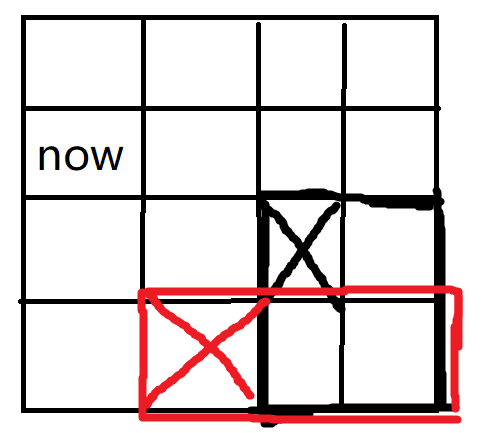
假设我们要在(now)这个点放一辆车,那么它只会对它右下角的点的(DP)值产生影响,并且下面这种已经放过车的右下方的位置的(DP)值也没有影响,所以我们要更新的点的数量就比较有限了。关于如何遍历这个奇形怪状的东西,我们只需要一行一行枚举,存一下当前遇到的最左边的车的横坐标,以后便利的横坐标都要小于这个值就行了)。另外我们要动态查询(f)的最大值,这个东西用一棵权值线段树当成平衡树跑就可以实现(log)级别,所以总的时间复杂度最劣是(O(n^2dlogn))的,但是只要随机它能飞起来。
(100pts:)简直精妙到不得了的,时间复杂度应该是最劣(n^2logn+mn)的。答案显然是递减的,并且答案的值域就只有([1,2000]),还是满足决策单调性的!这就使人浮想联翩了。由于加上一辆车可能会破坏很多答案,破坏性质不优美,即使用平衡树维护啥的都很吃力,所以我们反过来想:我们移走一辆车,看看包括它的矩形最大是多少的,这个时候两个答案取(max)是满足交换律的,相当优美。
但是光光这样还是相当困难。我们再加上一个小小的转换:记录上一次的答案是(lastans),那么我这次就依次验证有没有矩形包含这个新空格且大小为(lastans+1)、(lastans+2)······直到不合法为止。这个可以用平衡树来解决:设(r1_{i,j})、(r2)、(r3)、(r4)分别是它向四个方向能延伸多少,那么我在指定空格的那个纵列上依次扫下来,看看这个高度为(lastans+1)的窗口内的向左、向右的最小值加起来是否能够大于等于(lastans+1)。显然一个空格只会影响它所在的那一横一竖的(r),暴力修改即可。
它的时间复杂度显然是均摊的,最劣是(n^2logn+mn),据说用并查集可以优化到(n^2alpha)的。
这启发我们在答案值域很小、满足单调性和决策单调性的时候可以使用反过来的、判定性的方法解决问题。