1.树的定义:
(1)有且只有一个称为根的节点。
(2)有若干个互不相交的子树,这些子树本身也是一棵树。
eg:

2.通俗的定义:
(1)树由节点和边组成。
(2)每个节点只有一个父节点但可以有多个子节点。
(3)根节点没有父节点。
3.树的一些名词:
(1)节点
(2)父节点
(3)子节点
(4)子孙
(5)堂兄弟
(6)深度:从根节点到最低层节点的层数称之为深度,根节点是第一层。
(7)叶子节点:没有子节点的节点。
(8)非终端节点:即非叶子节点。
(9)度:子节点的个数成为度。(树的度为整个树中含有最多子节点的个数。)
4.树的分类:
(1)一般树:任意一个节点的子节点个数都不受限制。
(2)二叉树:(有序树)任意节点的子节点个数最多只有两个,且子节点的位置不可更改。(左子节点,右子节点的位置不可更改)
二叉树的分类:
a.一般二叉树
b.满二叉树:在不增加树的层次的前提下,无法再添加一个节点的二叉树。
(3)完全二叉树:如果只是删除满二叉树最底层最右边的连续若干个节点,这样形成的二叉树就是完全二叉树。
eg:

满二叉树是完全二叉树的一个特例。
5.树的存储
(1)二叉树的存储
a.连续存储(完全二叉树)
b.链式存储
eg:如果只是保存树的有效节点,无法知道原本的树的结构。

6.二叉树是非线性的数据结构,在存储时,把非线性转化为线性,有以下三种方法:
(1)先序遍历
(2)中序遍历
(3)后序遍历
7.将普通树转化为完全二叉树,用数组来存储二叉树的优点:
(1)已知节点的个数就可以知道层数。
(2)已知节点的编号,可以知道父节点和子节点。
(3)查找某个节点的父节点和子节点。(包括判断有没有)
缺点:占用内存过大。
8.链式存储
n个节点,浪费n+1空间(线性浪费)。
9.一般树的存储
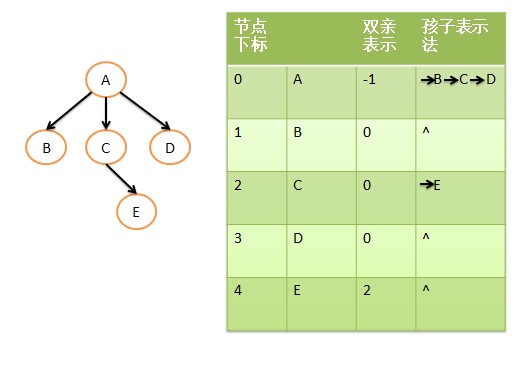
(1)双亲表示法(求父节点方便)

(2)孩子表示法(求子节点方便)

(3)双亲孩子表示法(求父节点和子节点都方便)
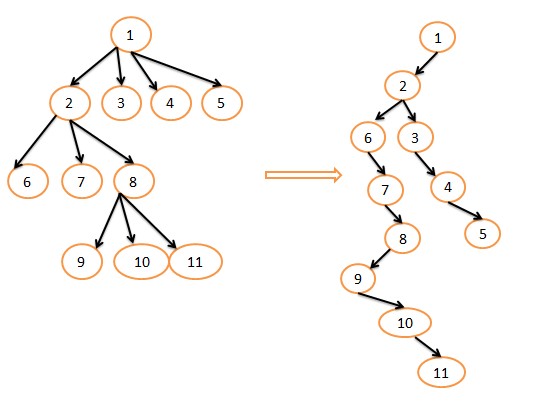
(4)二叉树表示法(也叫孩子兄弟链表表示法)
把一个普通树转化为二叉树来存储。具体的转化方法:设法保证任意一个节点的左指针域指向它的第一个孩子,右指针域指向它的下一个兄弟。
eg:
10.森林的存储——转化为二叉树存储
以下三棵树组成森林:
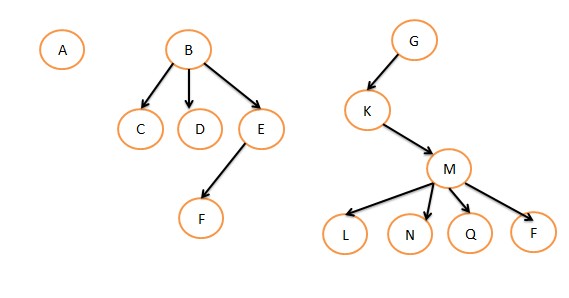
转化为二叉树:

11.二叉树的操作
(1)遍历。
(2)已知两种遍历序列求原始二叉树。
12.遍历分以下三种:
(1)先序遍历:先访问根节点,再先序访问左子树,再先序访问右子树。

先序:A-B-D-E-C-F-G
(2)中序遍历:[中间访问根节点]中序遍历左子树,再访问根节点,再中序遍历右子树。
eg:

中序:B-D-C-E-A-L-F-N-Q-M
eg:

中序:B-D-C-A-M-Q-E-L-N
(3)后序遍历:[最后访问根节点]先后序遍历左子树,在后序遍历右子树,再访问根节点。
eg:

后序:B-D-M-F-L-E-C-A
13.已知两种遍历序列求原始二叉树
已知先序遍历和中序遍历,或是已知中序遍历和后序遍历可以推算出原始二叉树。注意:已知先序和后序是不能推算出原始二叉树的。
eg:(1)已知先序和中序求后序。
先序:ABCDEFGH
中序:BDCEAFHG
求后序?
解题思路:先序中最先出现的是根节点,从中序可以确定左右子树,然后再在先序中确立接下里的根节点。
后序:DECBHGFA

(2)已知中序和后序求先序。
中序:BDCEAFHG
后序:DECBHGFA
求先序?
解题思路:先根据后序找到根节点,然后根据中序找到左右子树,在后序中最后出现的为根节点。
先序:ABCDEFGH

14.树的应用
(1)树是数据库中数据组织的一种重要形式。eg:图书馆图书的分类。
(2)操作系统子父进程的关系本身就是一棵树。
(3)面向对象语言中类的继承关系本身就是一棵树。
(4)赫夫曼树。