在神经网络中,广泛的使用反向传播和梯度下降算法调整神经网络中参数的取值。
梯度下降和学习率:
假设用 θ 来表示神经网络中的参数, J(θ) 表示在给定参数下训练数据集上损失函数的大小。
那么整个优化过程就是寻找一个参数θ, 使得J(θ) 的值最小, 也就是求J(θ) 的最小值
损失函数J(θ)的梯度 = ∂ J(θ) / ∂ θ
此时定义一个学习率 η
梯度下降法更新参数的公式为: θn+1 = θn - η ( ∂ J(θn) / ∂ θn )
将这个公式循环的重复下去,θ的值就从高处逐渐向最低处一小步一小步的移动
举个例子:
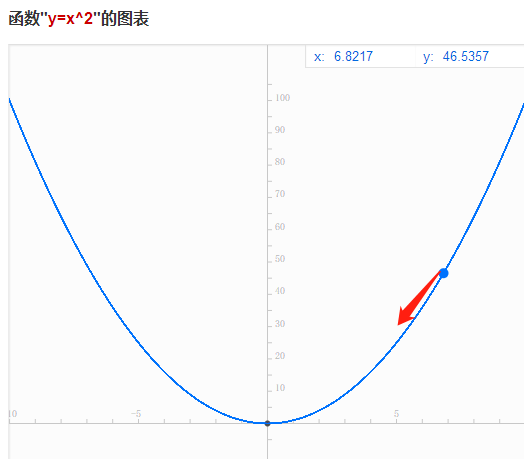
使用梯度下降 使得损失函数函数 J(x) = x2 的值尽量小, 由二次函数图像开口向上可以知道,二次函数最小值为0,
梯度 ▽ = ∂ J(x) / ∂ x = 2x
假设初始值为 x= 5, 设置学习率为0.3
使用梯度下降更新x的值 步骤如下:
轮数 当前参数x 梯度 * 学习率 更新后参数
1 5 2*5*0.3 = 3 5-3=2
2 2 2*2*0.3 = 1.2 2-1.2 = 0.8
3 0.8 2*0.8*0.3 = 0.48 0.8-0.48 = 0.32
4 0.32 2*0.32*0.3 = 0.192 0.32-0.192=0.128
5 0.128 2*0.128*0.3=0.0768 0.128-0.0768=0.0512
经过五次迭代x从5变成了0.0512, 已经和0非常接近了。
但是梯度下降并不能每次都能获得全局最优解。
如果学习率过小,可能会导致陷入局部最优解的情况。如图:

如果学习率过大,很可能在最优解两侧来回回荡,永远也到不了最低点。
举个例子:
使用梯度下降 使得损失函数函数 J(x) = x2 的值尽量小, 由二次函数图像开口向上可以知道,二次函数最小值为0,
梯度 ▽ = ∂ J(x) / ∂ x = 2x
假设初始值为 x= 5, 设置学习率为 1
使用梯度下降更新x的值 步骤如下:
轮数 当前参数x 梯度 * 学习率 更新后参数
1 5 2*5*1= 10 5-10 = -5
2 -5 2*-5*1 =-10 -5+10 = 5
继续下去他仍会来回摆荡,永远无法收敛
可见, 学习率过大或者过小都不好。
tensorflow为我们提供了一种灵活的学习率设置方式----指数衰减: tf.train.exponential_decy函数
每一轮的学习率 = 学习率 * 衰减系数^(global_steps/decay_steps)
随着步数的增加,学习率在变小,并且步数越多,变小的速度越慢
learning_rate = tf.train.exponential_decay(学习率, global_step, decay_step, 衰减系数,staircase=True)
global_step 是当前已经执行多少步了
decay_step 是下降速度,指的是 每隔多少步,学习率指数增长一个
例如:
tf.train.exponential_decay(0.1, global_step, 100, 0.96,staircase=True)
初始学习率0.1 每隔100步 学习率乘以0.96
stairecase 为true的时候,以阶梯方式下降, 为False时候 以平滑曲线下降