引言、
最近在看周志华老师的《机器学习》,期间在主成分分析和降维学习方面经常出现样本协方差矩阵的计算,这里对这一部分知识进行查阅和辨析,以便以后学习阶段的理解。
样本与随机变量
样本的获取可以看作是随机变量的采集过程。我们将两者的区别尽可能放大:
随机变量:此时我们已经知道了变量的分布情况,即假设知道了nature of system。我们可以通过期望值来计算方差、协方差以及协方差矩阵。
样本:然而事与愿违,大部分科研研究所获得的数据并不是随机变量——我们并不事先知道变量的分布情况(否则还研究什么??),所以只能通过收集到的样本信息去估计unknown nature of system。因此,样本协方差(sample covariance)更加常见。
根据数理统计课本中的定义:X1,X2,X3,……,Xn相互独立且都与总体X同分布,则称X1,X2,X3,……,Xn为来自总体X的简单随机样本,简称样本。n为样本容量。(至于为什么需要相互独立你可以理解为定义方便,这样子在后续的应用中,如极大似然估计,方便运用)。
样本X1,X2,X3,……,Xn的数字特征:
(1)样本均值

(2)样本方差

(3)样本标准差
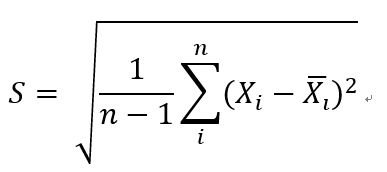
通常,我们根据样本均值和样本方差来估计随机变量的均值和方差:
如果总体X有数学期望E(x)=μ,则![]()
如果总体X有方差D(X),则![]()
协方差、
在提到协方差时,我们通常说的是两部分:(1)随机变量的协方差。跟数学期望、方差一样,是分布的一个总体参数。(2)样本的协方差。是样本集的一个统计量,可作为联合分布总体参数的一个估计。在实际中计算的通常是样本的协方差。
引用一下博主 苦力笨笨 博客 https://www.cnblogs.com/terencezhou/p/6235974.html
在上述博客中对于随机变量、样本的协方差、协方差矩阵四个部分有了较为全面的讲解。具体的讲解大家可以转至上述链接。