20172323 2018-2019-1 《程序设计与数据结构》第一周学习总结
教材学习内容总结
第一章——概述
-
1.1 软件质量
-
软件工程(Software Engineering)是一门关于高质量软件开发的技术和理论的学科。
-
解决的问题:控制开发过程,实现高质量的软件
-
软件工程的目标

-
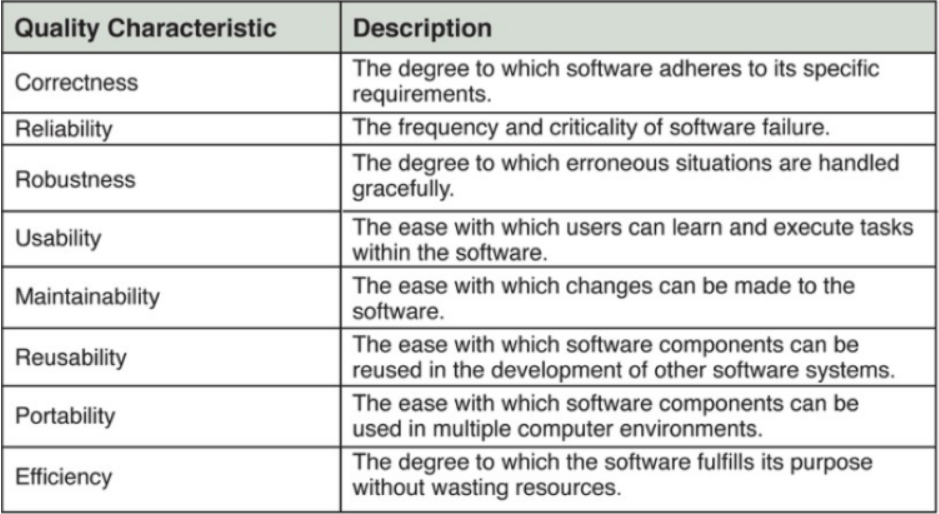
高质量软件的特征
-
-
1.2 数据结构
- 数据结构:计算机存储、组织数据的形式。
程序 = 数据结构 + 算法
软件 = 程序 + 软件工程 - 栈会颠倒数据的顺序,而队列可以保持数据的顺序。
- 数据结构:计算机存储、组织数据的形式。
第二章——算法分析
- 算法效率分析
- 算法分析是计算机科学的基础
- 增长函数与大O记法
- 增长函数(growth function)表示与该问题大小相对应的时间或空间的使用。表示问题(n)大小与我们希望最优化的值之间的关系。表示了该算法的时间复杂度或空间复杂度。
- 渐进复杂度(asymptotic complexity)称为算法的阶次,随着问题大小的增加时增长函数的一般性质,这一性质取决于该表达式的主项,即n增加时表达式中增长最快的那一项。算法的阶次是忽略该算法的增长函数中的常量和其他次要项,只保留主项而得出的。算法的阶次为增长函数提供了一个上界。
第二个洗盘子算法具有阶次为n2的时间复杂度,记为O(n^2)。第一个洗盘子的事例,其增长函数为t(n)=60n,其阶次为n,记为O(n)。
-
这种记法称为O(n)或大O记法。无论问题是大是小,运行赋值语句和if语句一次,其复杂度就为O(1)。
-
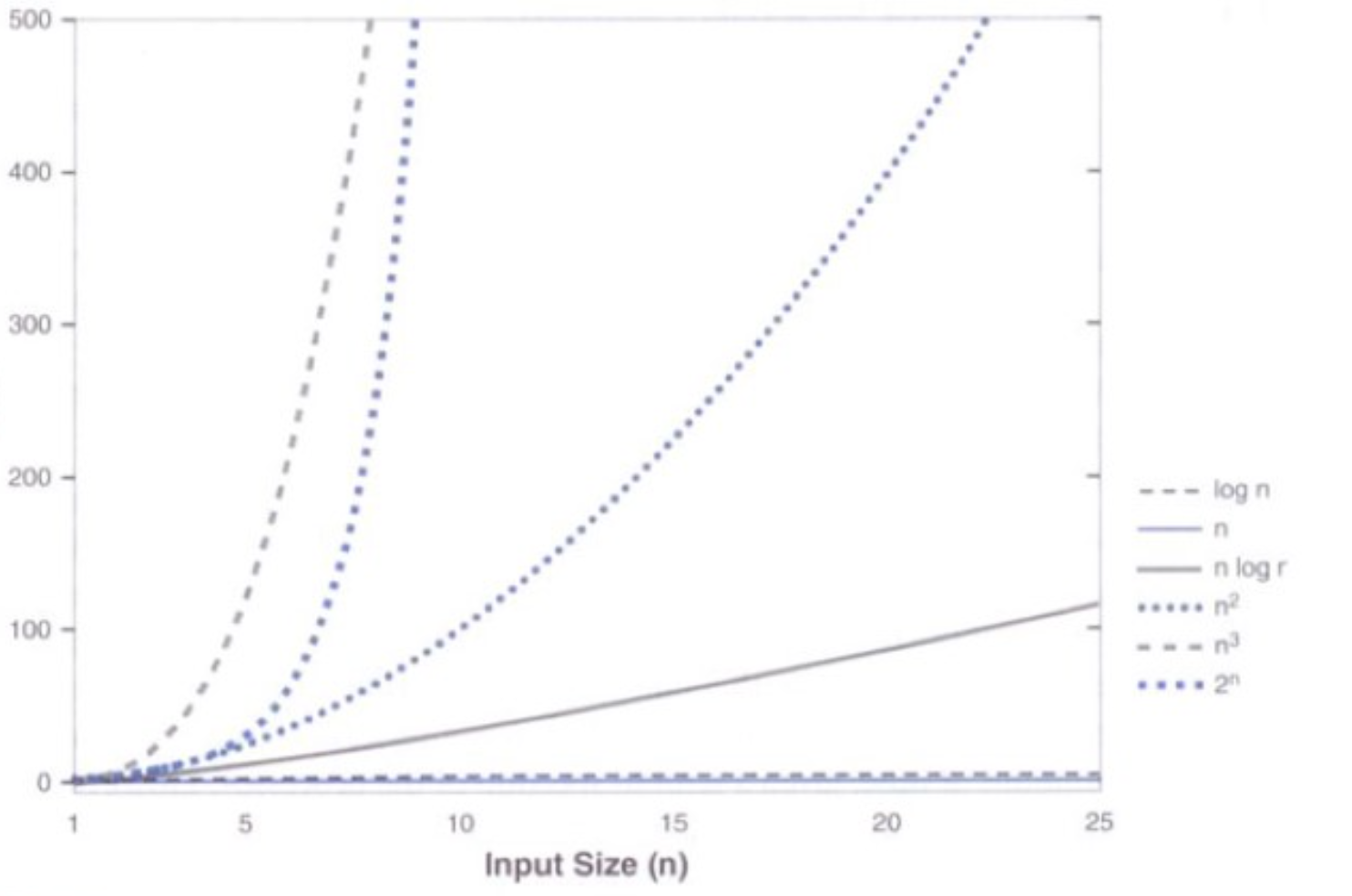
增长函数的比较
- 处理器速度的提高只会给增长函数添加常量。如果算法的运行速率低,那么从长远来说,使用更快的处理器也无济于事。

如图,处理器速度提高10倍,时间复杂度为n^2的B算法的运行效率仅仅提升了3.16倍,即10的平方根倍。
- 处理器速度的提高只会给增长函数添加常量。如果算法的运行速率低,那么从长远来说,使用更快的处理器也无济于事。
-
增长函数的比较图
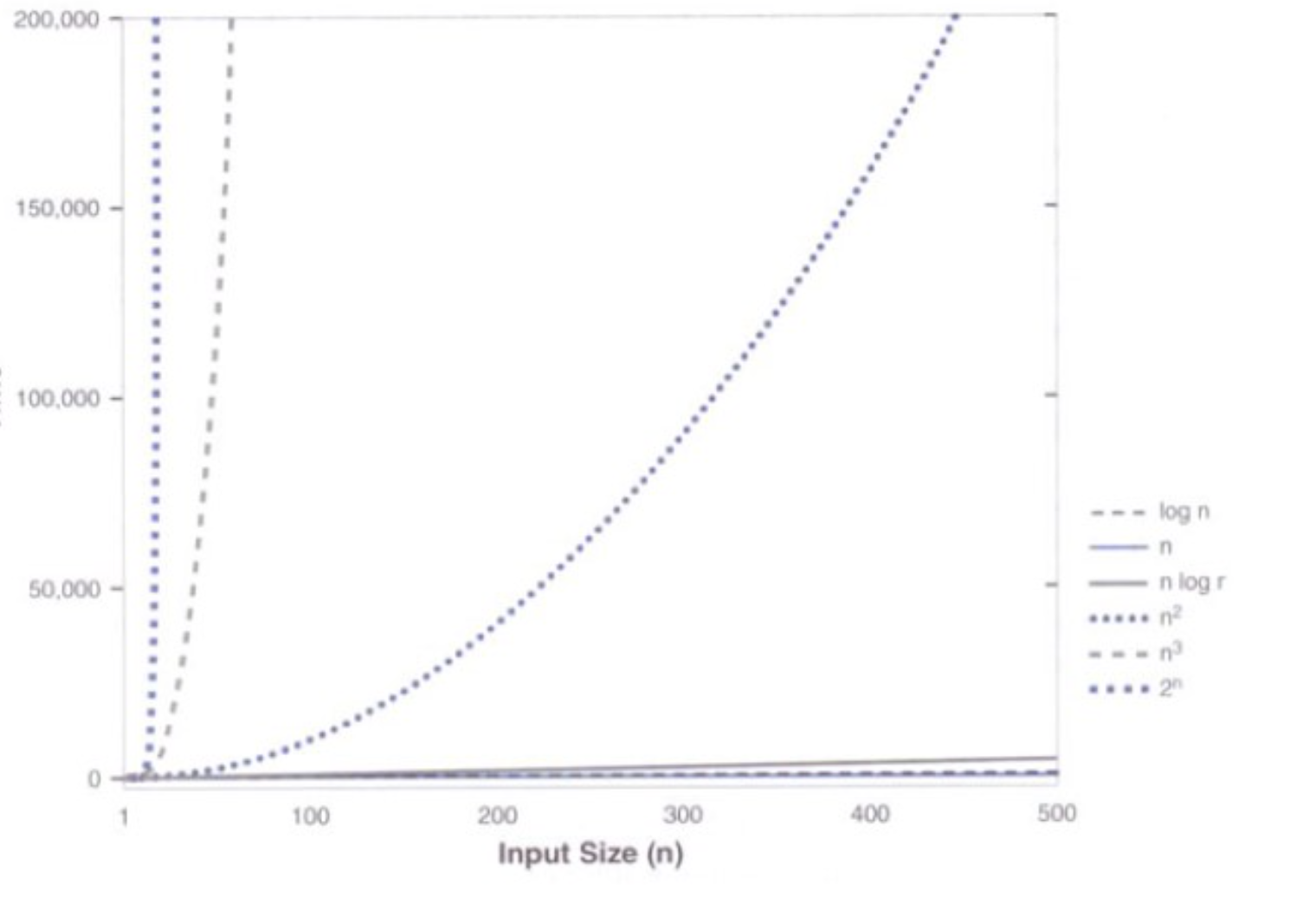
- 时间复杂度分析
- 循环运行的复杂度分析:要确定某个算法的阶次,常常需要确定某个特定语句或某个语句集运行的次数。
eg1假设某个循环体的复杂度为O(1),那么下面循环的时间复杂度为O(n)
- 循环运行的复杂度分析:要确定某个算法的阶次,常常需要确定某个特定语句或某个语句集运行的次数。
for (int count = 0; count < n; count++)
{
// 复杂度为O(1)的步骤系列
}
eg2如果该循环的复杂度是对数级的,则该循环是O(logn)
count = 1;
while(count < n)
{
count *=2;
//复杂度为O(1)的步骤系列
}
- 嵌套循环的复杂度分析
eg3下例中,内层循环体的复杂度为O(1),并且该内层循环将运行n次,则其复杂度为O(n^2)。
for(int count = 0;count < n;count++)
{
for(int count2 = 0;count2<n;count2++)
{
//复杂度为O(1)的步骤系列
}
}
- 方法调用的复杂度分析
eg4时间复杂度为O(n^2)
for(int count = 0;count<n;count++)
{
printsum(count);
}
public void printsum(int count)
{
int sum = 0;
for(int I = 1;I<count;I++)
sum += I;
System.out.println(sum);
}
- 时间复杂度的计算规则
-
加法规则
T(n,m) = T1(n) + T2(n) = O (max ( f(n), g(m) ) -
乘法规则
T(n,m) = T1(n) * T2(m) = O (f(n) * g(m)) -
一个特例(问题规模为常量的时间复杂度)
在大O表示法里面有一个特例,如果T1(n) = O(c), c是一个与n无关的任意常数,T2(n) = O ( f(n) ) 则有T(n) = T1(n) * T2(n) = O ( c*f(n) ) = O( f(n) )。也就是说,在大O表示法中,任何非0正常数都属于同一数量级,记为O(1)。
教材学习中的问题和解决过程
- 问题1:高质量软件的两个特征可重用性和可移植性有什么区别
- 问题1解决方案:就概念而言,一个是指软件组件可重用于其他软件系统开发的难易程度,一个是指软件组件可以在多个计算机环境下使用的难易程度。
课后习题解答
-
EX 2.1:下列增长函数的阶次是多少?
a.10n^2+100n+1000
解答:阶次为n^2
b.10n^3-7
解答:阶次为n^3
c.2n+100n3
解答:阶次为n^3
d.n^2 ·log(n)
解答:阶次为n^2 ·log(n) -
EX 2.4:请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
for(int count2 = 0 ; count2 < n ; count2 = count2 + 2)
{
System.out.println(count,count2);
}
}
解答:内循环循环n/2次,外循环循环n次,故增长函数为F(n)=(n2)/2,阶次为n2。
- EX 2.5:请确定下面代码段的增长函数和阶次
for(int count = 0 ; count < n ; count++)
for(int count2 = 1 ; count2 < n ; count2 = count2 * 2)
{
System.out.println(count,count2);
}
}
解答:外层循环n次,内层循环log₂(n-1)次。故增长函数为F(n)=nlog₂(n-1),阶次为nlog₂(n-1)。
其他(感悟、思考等,可选)
上学期的Java课没有打下坚实的基础,但我还是王老师课上说的,亡羊补牢,为时不晚。希望这个学期能够善始善终,努力学好专业知识,学有所用。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 8/8 |
结对及互评
- 基于评分标准,我给谭鑫的博客打分:7分。得分情况如下:
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, 三个问题加3分
代码调试中的问题和解决过程, 无问题
感想,体会不假大空的加1分
点评认真,能指出博客和代码中的问题的加1分 - 基于评分标准,我给方艺雯的博客打分:4分。得分情况如下:
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
感想,体会不假大空的加1分
点评认真,能指出博客和代码中的问题的加1分