题目链接:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3640
题意:
有一个吸血鬼被困住了,他要逃跑。。。
他面前有n条路,每条路有一个困难程度c[i]。
他的初始攻击力为f。
每天他会从中随机选一条路:
(1)如果当前攻击力 > c[i],那么他会再花t天走这条路成功逃跑(t的公式如图)。
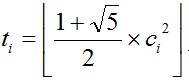
(2)攻击力 <= c[i],这条路他走不过去,但可以让他的攻击力 += c[i]。
问你成功逃跑所需天数的期望。
题解:
表示状态:
dp[i] = expected time(攻击力为i时,逃跑还需要的天数)
找出答案:
ans = dp[f]
初始攻击力为f。
如何转移:
对于每一条路,每一次被选择的概率都为1/n。
当前攻击力为i,枚举每一条路j,则:
(1)if i > c[j]: dp[i] += t/n (可以用t天逃跑)
(2)else: dp[i] += (dp[i+c[j]]+1)/n (攻击力增加c[j]后所用天数 + 今天一天)
边界条件:
对于一个攻击力max_atk满足max_atk > 所有的c[i],则所有的dp[max_atk]都相等。
(因为只能逃跑,不能再攒攻击力了)
所以找出满足条件的最小的max_atk,max_atk = max( max(c[i]), f )。
可能用到的攻击力最大为max_atk*2。
(根据Code: "else dp[i]+=(dp[i+c[j]]+1)/n")
所以按从max_atk*2到f的顺序求dp就行了。
初始值(设成啥都行。。。没用):set dp = 0
AC Code:
1 // state expression: 2 // dp[i] = expected time 3 // i: present atk 4 // 5 // find the answer: 6 // ans = dp[f] 7 // 8 // transferring: 9 // now: dp[i] 10 // enum: c[j] 11 // if i > c[j] dp[i] += t/n 12 // else dp[i] += (dp[i+c[j]]+1)/n 13 // 14 // boundary: 15 // set dp = 0 16 #include <iostream> 17 #include <stdio.h> 18 #include <string.h> 19 #include <math.h> 20 #define MAX_N 105 21 #define MAX_F 30005 22 23 using namespace std; 24 25 int n,f; 26 int max_atk; 27 int c[MAX_N]; 28 double dp[MAX_F]; 29 30 void read() 31 { 32 max_atk=f; 33 for(int i=0;i<n;i++) 34 { 35 cin>>c[i]; 36 max_atk=max(max_atk,c[i]); 37 } 38 } 39 40 void solve() 41 { 42 memset(dp,0,sizeof(dp)); 43 for(int i=max_atk*2+100;i>=f;i--) 44 { 45 for(int j=0;j<n;j++) 46 { 47 if(i>c[j]) dp[i]+=floor((1.0+sqrt(5))/2.0*c[j]*c[j])/n; 48 else dp[i]+=(dp[i+c[j]]+1)/n; 49 } 50 } 51 } 52 53 void print() 54 { 55 printf("%.3f ",dp[f]); 56 } 57 58 int main() 59 { 60 while(cin>>n>>f) 61 { 62 read(); 63 solve(); 64 print(); 65 } 66 }