LightOJ 1132 Summing up Powers：矩阵快速幂 + 二项式定理

题目链接：http://lightoj.com/volume_showproblem.php?problem=1132

题意：

　　给定n、k，求(1^K + 2^K + 3^K + ... + N^K) % 2³²。

 

题解：

　　设sum(i) = 1^K + 2^K + 3^K + ... + i^K

　　所以要从sum(1)一直推到sum(n)。

　　所以要找出sum(i)和sum(i+1)之间的关系：

　　

　　

　　

　　好了可以造矩阵了。

　　（n = 6时）

　　矩阵表示（大小为 1 * (k+2)）：

　　

　　

　　初始矩阵start：

　　

　　也就是：

　　

　　

 　　特殊矩阵special：

　　

 

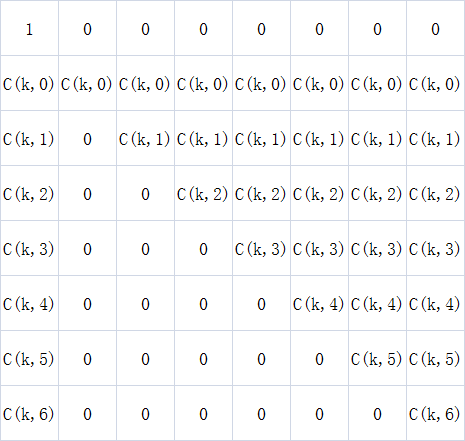
AC Code:

#include <iostream>
#include <stdio.h>
#include <string.h>
#define MAX_L 60
#define MAX_K 55

using namespace std;

struct Mat
{
    int n;
    int m;
    unsigned val[MAX_L][MAX_L];
    Mat()
    {
        n=0;
        m=0;
        memset(val,0,sizeof(val));
    }
    void print_mat()
    {
        cout<<"--------"<<endl;
        for(int i=0;i<n;i++)
        {
            for(int j=0;j<m;j++)
            {
                cout<<val[i][j]<<" ";
            }
            cout<<endl;
        }
        cout<<"--------"<<endl;
    }
};

int k,t;
long long n;
unsigned c[MAX_K][MAX_K];

void cal_combination()
{
    memset(c,0,sizeof(c));
    c[0][0]=1;
    for(int i=1;i<MAX_K;i++)
    {
        c[i][0]=1;
        for(int j=1;j<=i;j++)
        {
            c[i][j]=c[i-1][j]+c[i-1][j-1];
        }
    }
}

Mat make_unit(int n)
{
    Mat mat;
    mat.n=n;
    mat.m=n;
    for(int i=0;i<n;i++)
    {
        mat.val[i][i]=1;
    }
    return mat;
}

Mat make_start(int k)
{
    Mat mat;
    mat.n=1;
    mat.m=k+2;
    for(int i=0;i<k+2;i++)
    {
        mat.val[0][i]=1;
    }
    return mat;
}

Mat make_special(int k)
{
    Mat mat;
    mat.n=k+2;
    mat.m=k+2;
    for(int j=1;j<k+2;j++)
    {
        for(int i=j;i<k+2;i++)
        {
            mat.val[i][j]=c[k-j+1][i-j];
        }
    }
    for(int i=1;i<k+2;i++)
    {
        mat.val[i][0]=mat.val[i][1];
    }
    mat.val[0][0]=1;
    return mat;
}

Mat mul_mat(const Mat &a,const Mat &b)
{
    Mat c;
    if(a.m!=b.n)
    {
        cout<<"Error: mul_mat"<<endl;
        return c;
    }
    c.n=a.n;
    c.m=b.m;
    for(int i=0;i<a.n;i++)
    {
        for(int j=0;j<b.m;j++)
        {
            for(int k=0;k<a.m;k++)
            {
                c.val[i][j]+=a.val[i][k]*b.val[k][j];
            }
        }
    }
    return c;
}

Mat quick_pow_mat(Mat mat,long long k)
{
    Mat ans;
    if(mat.n!=mat.m)
    {
        cout<<"Error: quick_pow_mat"<<endl;
        return ans;
    }
    ans=make_unit(mat.n);
    while(k)
    {
        if(k&1)
        {
            ans=mul_mat(ans,mat);
        }
        mat=mul_mat(mat,mat);
        k>>=1;
    }
    return ans;
}

int main()
{
//    freopen("in.txt","r",stdin);
//    freopen("out.txt","w",stdout);
    cal_combination();
    cin>>t;
    for(int cas=1;cas<=t;cas++)
    {
        cin>>n>>k;
        Mat start=make_start(k);
        Mat special=make_special(k);
        Mat ans=mul_mat(start,quick_pow_mat(special,n-1));
        cout<<"Case "<<cas<<": "<<ans.val[0][0]<<endl;
    }
}