题目链接:http://lightoj.com/volume_showproblem.php?problem=1070
题意:
给你a+b和ab的值,给定一个n,让你求a^n + b^n的值(MOD 2^64)。
题解:
a + b也就是a^1 + b^1,然后要从这儿一直推到a^n + b^n。
矩阵快速幂?o( ̄▽ ̄)d
那么主要解决的就是如何从a^n + b^n推到a^(n+1) + b^(n+1)。
下面是推导过程:
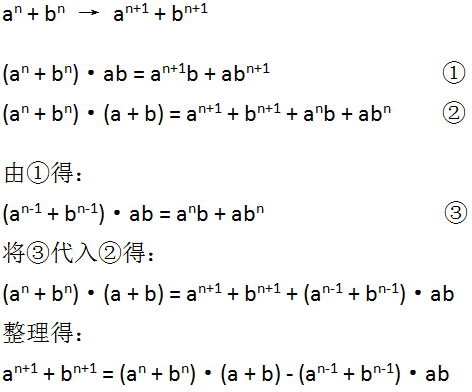
由于推a^(n+1) + b^(n+1)要用到a^n + b^n和a^(n-1) + b^(n-1),所以初始矩阵为1*2大小,为[a^0+b^0, a^1+b^1]。
初始矩阵start:

特殊矩阵special:

所求矩阵ans:
ans = start * special^n
ans的第一项即为a^n + b^n.
注:由于题目要求MOD 2^64,所以直接将矩阵内元素定义为unsigned long long类型,自然溢出就好啦。
AC Code:
1 #include <iostream>
2 #include <stdio.h>
3 #include <string.h>
4 #define MAX_L 5
5
6 using namespace std;
7
8 struct Mat
9 {
10 int n;
11 int m;
12 unsigned long long val[MAX_L][MAX_L];
13 Mat()
14 {
15 n=0;
16 m=0;
17 memset(val,0,sizeof(val));
18 }
19 };
20
21 int p,q,n,t;
22
23 Mat make_unit(int n)
24 {
25 Mat mat;
26 mat.n=n;
27 mat.m=n;
28 for(int i=0;i<n;i++)
29 {
30 mat.val[i][i]=1;
31 }
32 return mat;
33 }
34
35 Mat make_start()
36 {
37 Mat mat;
38 mat.n=1;
39 mat.m=2;
40 mat.val[0][0]=2;
41 mat.val[0][1]=p;
42 return mat;
43 }
44
45 Mat make_special()
46 {
47 Mat mat;
48 mat.n=2;
49 mat.m=2;
50 mat.val[0][0]=0;
51 mat.val[0][1]=-q;
52 mat.val[1][0]=1;
53 mat.val[1][1]=p;
54 return mat;
55 }
56
57 Mat mul_mat(const Mat &a,const Mat &b)
58 {
59 Mat c;
60 if(a.m!=b.n)
61 {
62 cout<<"Error: mul_mat"<<endl;
63 return c;
64 }
65 c.n=a.n;
66 c.m=b.m;
67 for(int i=0;i<a.n;i++)
68 {
69 for(int j=0;j<b.m;j++)
70 {
71 for(int k=0;k<a.m;k++)
72 {
73 c.val[i][j]+=a.val[i][k]*b.val[k][j];
74 }
75 }
76 }
77 return c;
78 }
79
80 Mat quick_pow_mat(Mat mat,long long k)
81 {
82 Mat ans;
83 if(mat.n!=mat.m)
84 {
85 cout<<"Error: quick_pow_mat"<<endl;
86 return ans;
87 }
88 ans=make_unit(mat.n);
89 while(k)
90 {
91 if(k&1)
92 {
93 ans=mul_mat(ans,mat);
94 }
95 mat=mul_mat(mat,mat);
96 k>>=1;
97 }
98 return ans;
99 }
100
101 int main()
102 {
103 cin>>t;
104 for(int cas=1;cas<=t;cas++)
105 {
106 cin>>p>>q>>n;
107 Mat start=make_start();
108 Mat special=make_special();
109 Mat ans=mul_mat(start,quick_pow_mat(special,n));
110 cout<<"Case "<<cas<<": "<<ans.val[0][0]<<endl;
111 }
112 }