习题
1、写出一个运行时间为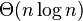 的算法,使之能在给定一个由n个整数构成的集合S和另一个整数时,判断出S中是否存在有两个其和等于x的元素。
的算法,使之能在给定一个由n个整数构成的集合S和另一个整数时,判断出S中是否存在有两个其和等于x的元素。
首先对集合进行排序,用归并排序(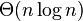 ),然后再从集合的第一个元素到最后一个元素,对集合进行二分查找,查找x减去该元素(
),然后再从集合的第一个元素到最后一个元素,对集合进行二分查找,查找x减去该元素(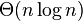 )
)
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 void merge(int A[], int p, int q, int r){ 5 int n1 = q - p + 1; 6 int n2 = r - q; 7 int i, j, k; 8 int *L = malloc(n1 * sizeof(int)); 9 int *R = malloc(n2 * sizeof(int)); 10 11 for(i = 0; i < n1; i++) 12 L[i] = A[p+i]; 13 for(j = 0; j < n2; j++) 14 R[j] = A[q+j+1]; 15 16 i = 0; 17 j = 0; 18 for(k = p; k <= r; k++){ 19 if(i < n1 && j < n2){ 20 if(L[i] <= R[j]){ 21 A[k] = L[i]; 22 i++; 23 } 24 else{ 25 A[k] = R[j]; 26 j++; 27 } 28 } 29 else if(i >= n1){ 30 A[k] = R[j]; 31 j++; 32 } 33 else if(j >= n2){ 34 A[k] = L[i]; 35 i++; 36 } 37 } 38 } 39 40 /*归并排序*/ 41 void merge_sort(int A[], int p, int r){ 42 if(p < r){ 43 int q = (p + r) / 2; 44 merge_sort(A, p, q); 45 merge_sort(A, q+1, r); 46 merge(A, p, q, r); 47 } 48 } 49 50 /*二分查找*/ 51 int binary_search(int A[], int length, int key) { 52 int p = 0; 53 int q = length -1; 54 int m; 55 while(p < q){ 56 m = (p + q) / 2; 57 if(A[m] > key) 58 q = m; 59 else 60 p = m + 1; 61 } 62 if(A[p] == key) 63 return p; 64 else 65 return -1; 66 } 67 68 /*检查集合中是否存在两个数之和为x*/ 69 int check_sum(int A[], int length, int sum) { 70 int i; 71 int x, y; 72 for(i = 0; i < length; i++){ 73 x = A[i]; 74 y = sum - x; 75 if(binary_search(A, length, y)) 76 return 1; 77 else 78 return -1; 79 } 80 } 81 82 int main() { 83 int num; 84 int i; 85 int sum; 86 printf("Input the number: "); 87 scanf("%d", &num); 88 int *arry = malloc( num * sizeof(int)); 89 90 for(i = 0; i < num; i++) 91 scanf("%d", &arry[i]); 92 merge_sort(arry, 0, num - 1); //进行排序 93 94 printf("Input the sum: "); 95 scanf("%d", &sum); 96 int flag = check_sum(arry, num, sum); 97 if(flag) 98 printf("Yes! "); 99 else 100 printf("No! "); 101 return 0; 102 }
2、关于分治策略:将原问题划分成为n个规模较小而结构与原问题相似的子问题,递归地解决这些子问题,然后再合并其结果,得到原问题的解。
给出一个算法,它能用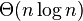 的最坏情况运行时间,确定n个元素的任何排列中的逆序对的数目。(提示:修改合并排序)
的最坏情况运行时间,确定n个元素的任何排列中的逆序对的数目。(提示:修改合并排序)
算导的提示是修改合并排序(归并排序),通过将数组分成小数组,先对小数组进行统计逆序对数目(左右两个将要合并的数组,如果右面的数组的第一个值比左面的小,就有逆序对。PS:小数组的顺序已经排好,所以逆序对的数目为左边数组的长度减去左边数组的第一个值的下标),然后合并两个小数组,接着继续合并数组知道还原为原来的数组长度。
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 int merge_inversion(int A[], int p, int q, int r){ 5 int n1 = q - p + 1; 6 int n2 = r - q; 7 int i, j, k; 8 int inversion = 0; 9 int *L = malloc(n1 * sizeof(int)); 10 int *R = malloc(n2 * sizeof(int)); 11 12 for(i = 0; i < n1; i++) 13 L[i] = A[p+i]; 14 15 for(j = 0; j < n2; j++) 16 R[j] = A[q+j+1]; 17 18 i = 0; 19 j = 0; 20 for(k = p; k <= r; k++){ 21 if(i < n1 && j < n2){ 22 if(R[j] < L[i]){ 23 inversion = inversion + (n1 -1) - i + 1; 24 A[k] = R[j]; 25 j++; 26 } 27 else{ 28 A[k] = L[i]; 29 i++; 30 } 31 } 32 else if(i >= n1){ 33 A[k] = R[j]; 34 j++; 35 } 36 else if(j >= n2){ 37 A[k] = L[i]; 38 i++; 39 } 40 } 41 return inversion; 42 } 43 44 int count_inversion(int A[], int p, int r){ 45 int inversion = 0; 46 if(p < r){ 47 int q = (p + r) / 2; 48 inversion += count_inversion(A, p, q); 49 inversion += count_inversion(A, q+1, r); 50 inversion += merge_inversion(A, p, q, r); 51 } 52 return inversion; 53 } 54 55 int main(){ 56 int num; 57 int i; 58 int sum; 59 printf("Input the number: "); 60 scanf("%d", &num); 61 int *arry = malloc( num * sizeof(int)); 62 63 for(i = 0; i < num; i++) 64 scanf("%d", &arry[i]); 65 66 int count = count_inversion(arry, 0, num-1); 67 68 printf("The number of inversion is : %d ", count); 69 70 return 0; 71 }
