启迪思维:二叉树
很多初级点的程序员会认为树结构无用论,也有初级程序员仅仅以为只有面试才会用到,还有自认为实际工作用不到(我身边工作好几年程序员懂树结构也没有几个),其实归根到底还是不清楚树的实际用途,下面分享我参加培训时候一个小尴尬。
因为项目数据量很大(有很多表数据量都上亿的),对写sql能力要求很高,项目组会经常组织些数据库方面的培训,前段时间又参加公司一个SQL原理分析的一个培训,在培训中讲师问“为什么SQL走索引查询速度很快呢?”,我直接大声说“索引底层数据结构是B树,查询的时候用二分查找”,结果整个大房间就我一个人声音,所有同事都看过来,场面有点尴尬。
上一篇文章分析树基本概念、名词解释、树三种遍历方式,今天继续来看二叉树各种名词概率,看这些名词概念,肯定是各种不爽,大概浏览下知道怎么回事就ok。
一:概念,下面这些内容摘自维基百科
在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有个结点;深度为k的二叉树至多有个结点;对任何一棵二叉树T,如果其终端结点数为,度为2的结点数为,则。
树和二叉树的三个主要差别:
树的结点个数至少为1,而二叉树的结点个数可以为0;
树中结点的最大度数没有限制,而二叉树结点的最大度数为2;
树的结点无左、右之分,而二叉树的结点有左、右之分。
完全二叉树和满二叉树
满二叉树:一棵深度为k,且有个节点成为满二叉树
完全二叉树:深度为k,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中序号为1至n的节点对应时,称之为完全二叉树
二:示例图
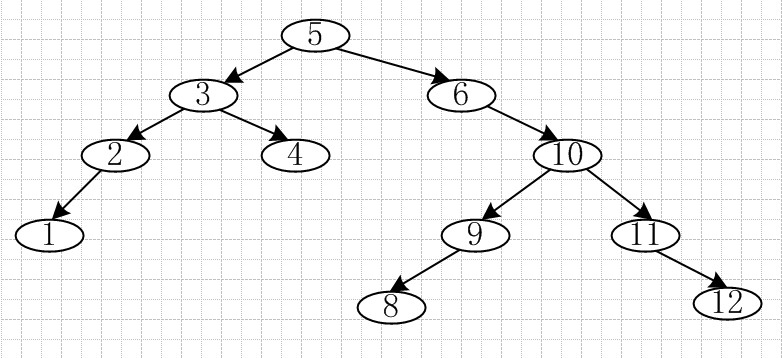
三:动画图
四:代码分析
1、是否为空
1 /** 2 * 若树为空,则返回true;否则返回false 3 */ 4 bool IsEmpty() { 5 return root == 0; 6 }
2、计算树的深度
1 /** 2 * 以传入节点为基础计算树的深度 3 */ 4 int GetTreeDept(const TNode<T> *t) { 5 int i, j; 6 if (t == 0) { 7 return 0; 8 } else { 9 //递归计算左子树的深度 10 i = this->GetTreeDept(t->lchild); 11 //递归计算右子树的深度 12 j = this->GetTreeDept(t->rchild); 13 } 14 15 //t的深度为其左右子树中深度中的大者加1 16 return i > j ? i + 1 : j + 1; 17 }
3、清空树的节点
1 /** 2 *清空树的所有节点 3 */ 4 void Clear() { 5 Clear(root); 6 } 7 8 /** 9 *根据节点递归清空树 10 */ 11 void Clear(TNode<T>* t) { 12 //判断指针是否为空 13 if (t) { 14 //获取资源立即放入管理对象(参考Effective C++里边条款13) 15 //tr1::shared_ptr(引用计数智慧指针)管理对象比auto_ptr更强大 16 std::auto_ptr<TNode<T> > new_ptr(t); 17 18 //递归清空右子树 19 Clear(new_ptr->rchild); 20 21 //递归清空左子树 22 Clear(new_ptr->lchild); 23 } 24 25 //清空树的根节点 26 t = 0; 27 }
4、获取树最大节点和最小节点
1 /** 2 *获取树的最大节点 3 */ 4 TNode<T>* GetMax(TNode<T>* t) const { 5 //判断数节点是否为空 6 if (t) { 7 //根据二叉树特性,最大值一定在右子树; 8 //循环右子树,直到叶子节点 9 while (t->rchild) { 10 //指向下一个节点 11 t = t->rchild; 12 } 13 } 14 //返回找到最大节点 15 return t; 16 } 17 /** 18 *获取树的最小节点 19 */ 20 TNode<T>* GetMin(TNode<T>* t) const { 21 //判断数节点是否为空 22 if (t) { 23 //根据二叉树特性,最大值一定在左子树; 24 //循环左子树,直到叶子节点 25 while (t->lchild) { 26 //指向下一个节点 27 t = t->lchild; 28 } 29 } 30 //返回找到最小节点 31 return t; 32 } 33 /** 34 *根据模式类型查找树的最大值或者最小值 35 */ 36 TNode<T>* GetNode(Mode mode) const { 37 //t指向根节点 38 TNode<T>* t = root; 39 //判断数节点是否为空 40 if (t) { 41 if (mode == Min) { 42 //根据二叉树特性,最大值一定在左子树; 43 //循环左子树,直到叶子节点 44 while (t->lchild) { 45 //指向左子树下一个节点 46 t = t->lchild; 47 } 48 } else if (mode == Max) { 49 //根据二叉树特性,最大值一定在右子树; 50 //循环右子树,直到叶子节点 51 while (t->rchild) { 52 //指向右子树下一个节点 53 t = t->rchild; 54 } 55 } 56 } 57 //返回找到节点 58 return t; 59 }
5、获取传入节点父节点
1 /** 2 *获取传入的节点从传入树p中找到它的父节点 3 */ 4 TNode<T>* GetParentNode(TNode<T> *p, const T &value,TNode<T> *returnValue) { 5 //p节点存在并且传入的值不是根节点值 6 if (p && p->data == value) { 7 return 0; 8 } 9 10 //用二分查找定位值value所在节点 11 TNode<T> *t = this->SearchTree(p, value); 12 13 //判断t和p都不为空 14 if (t && p) { 15 //如果value的节点等于p节点左孩子或者右孩子,p就是value的节点父亲 16 if (p->lchild == t || p->rchild == t) { 17 //赋值p节点给返回值变量 18 returnValue = p; 19 } else if (value > p->data) {//如果value只大于p节点值,则递归右孩子 20 //直到找到value的父节点复制给返回值变量 21 returnValue = GetParentNode(p->rchild, value,returnValue); 22 } else {////如果value只小于p节点值,则递归左孩子 23 //直到找到value的父节点复制给返回值变量 24 returnValue = GetParentNode(p->lchild, value,returnValue); 25 } 26 } 27 28 return returnValue; 29 30 } 31 32 /** 33 *获取传入的节点的父节点 34 */ 35 TNode<T>* GetParentNode(const T &value,TNode<T> *returnValue) { 36 return this->GetParentNode(root, value,returnValue); 37 }
6、二分查找
代码分析:
1 /** 2 * 在以T为根节点的树中搜索值为value的节点 3 */ 4 TNode<T>* SearchTree(TNode<T>* &t, const T &value) { 5 //判断t节点是否为空 6 while (t) { 7 //如果节点值等于value,则表明已经找到目标节点 8 if (t->data == value) { 9 return t; 10 } else if (value > t->data) {//如果value大于t节点值,则递归查询右子树 11 return SearchTree(t->rchild, value); 12 } else {//如果value小于t节点值,则递归查询左子树 13 return SearchTree(t->lchild, value); 14 } 15 } 16 return t; 17 }
动画演示:
7、插入节点
代码分析:
1 /** 2 *插入一个节点到目标树中 3 */ 4 void Insert(const T &value, TNode<T>* &t) { 5 //如果目标树为空,则新new一个根节点 6 if (t == 0) { 7 //新创建一个节点,并把value设置为节点值 8 t = new TNode<T>(value); 9 } else if (value < t->data) {//如果value值小于t节点值 10 //递归左子树插入函数,直到找到节点插入 11 this->Insert(value, t->lchild); 12 } else if (value > t->data) {//如果value值大于t节点值 13 //递归右子树插入函数,直到找到节点插入 14 this->Insert(value, t->rchild); 15 } 16 } 17 /** 18 *插入一个节点到根节点为root的树中 19 */ 20 void Insert(const T &value) { 21 this->Insert(value, root); 22 }
动画演示
8、删除节点
代码分析:
1 /** 2 *根据节点值删除节点信息 3 */ 4 void Delete(const T &value) { 5 Delete(value, root); 6 } 7 /** 8 *根据节点值删除以传入t为根节点树节点信息 9 */ 10 void Delete(const T &value, TNode<T>* &t) { 11 //判断是否t为空null 12 if (t) { 13 //通过二分查找定位value所在的节点 14 TNode<T> *p = this->SearchTree(t, value); 15 //中间变量,用于待删除节点左右子树都不为空的情况下 16 TNode<T> *q = p; 17 if (p) { 18 //如果p节点的左右孩子都不为空,则根据二叉树定义 19 //必须在子右子树中找到最新节点作为新节点 20 //当左右子树都为空情况下,右子树最小节点就是树(中序遍历)节点的后继节点 21 if (p->lchild != 0 && p->rchild != 0) { 22 //获取右子树中最小的节点 23 q = this->GetMin(p->rchild); 24 } 25 //获取资源立即放入管理对象(参考Effective C++里边条款13) 26 //tr1::shared_ptr(引用计数智慧指针)管理对象比auto_ptr更强大 27 //如果p节点的左右子树都不为空,则释放p节点子右子树的最小节点 28 //改变p节点的值即可 29 auto_ptr<TNode<T> > new_ptr(q); 30 31 TNode<T> *parent = 0; 32 TNode<T> *returnValue; 33 //删除叶子节点(节点左右孩子都为空) 34 if (p->lchild == 0 && p->rchild == 0) { 35 //如果p节点和传入的根节点相等 36 if (t == p) { 37 //直接设置t为空 38 t = 0; 39 } else { 40 //获取p节点的父节点 41 parent = this->GetParentNode(t, p->data,returnValue); 42 43 //如果父节点的左孩子等于p节点 44 if (parent->lchild == p) { 45 //设置父节点的左孩子等于空 46 parent->lchild = 0; 47 } else {//如果父节点的右孩子等于p节点 48 //设置父节点的右孩子等于空 49 parent->rchild = 0; 50 } 51 } 52 53 } else if (p->rchild == 0) {//删除节点p右孩子为空,左孩子有节点 54 //如果p节点和传入的根节点相等 55 if (t == p) { 56 //直接设置t节点等于左孩子 57 t = t->lchild; 58 } else { 59 //获取p节点的父节点 60 parent = this->GetParentNode(t, p->data,returnValue); 61 //如果父节点的左孩子等于p节点 62 if (parent->lchild == p) { 63 //设置父节点左孩子等于p节点左孩子 64 parent->lchild = p->lchild; 65 } else {//如果父节点的右孩子等于p节点 66 //设置父节点右孩子等于p节点左孩子 67 parent->rchild = p->lchild; 68 } 69 } 70 71 } else if (p->lchild == 0) {//删除节点p左孩子为空,右孩子有节点 72 //如果p节点和传入的根节点相等 73 if (t == p) { 74 //直接设置t节点等于右孩子 75 t = t->rchild; 76 } else { 77 //获取p节点的父节点 78 parent = this->GetParentNode(t, p->data,returnValue); 79 //如果父节点的右孩子等于p节点 80 if (parent->rchild == p) { 81 //设置父节点右孩子等于p节点右孩子 82 parent->rchild = p->rchild; 83 } else {//如果父节点的左孩子等于p节点 84 //设置父节点右孩子等于p节点右孩子 85 parent->lchild = p->rchild; 86 } 87 } 88 } else {//删除节点p左右都有孩子 89 //获取q节点的父节点 90 parent = this->GetParentNode(t,q->data,returnValue); 91 //设置p节点值等于q节点值 92 p->data = q->data; 93 //如果q的父节点等于p 94 if (parent == p) { 95 //设置q节点的父节点右孩子为q节点右孩子 96 parent->rchild = q->rchild; 97 } else {// 98 //设置q节点的父节点左孩子为q节点右孩子 99 parent->lchild = q->rchild; 100 } 101 102 } 103 } 104 } 105 }
动画演示
9、获取目标节点后继节点(中序遍历)
1 /** 2 *在传入p的树中找出节点值为value的后继节点方法 3 */ 4 TNode<T>* TreeSuccessor(TNode<T> *p,const T &value,TNode<T> *returnValue){ 5 //如果t节点非空 6 if(p){ 7 //传入p树和节点值value找到对应的节点 8 TNode<T> *t = this->SearchTree(p, value); 9 //如果节点右子树不为空 10 if(t->rchild != 0){ 11 //直接获取右子树中最小节点,即是节点的后继节点 12 returnValue = this->GetMin(t->rchild); 13 }else{ 14 //获取目标节点父节点 15 TNode<T> *parent = this->GetParentNode(t->data,returnValue); 16 17 //如果父节点不为空并且t节点等于父节点的右节点,这一个文字不太好描述,请参照图 18 while(parent && t == parent->rchild){ 19 //父节点赋值给t节点 20 t = parent; 21 //获取父节点的父节点(目标节点爷爷) 22 parent = this->GetParentNode(parent->data,returnValue); 23 } 24 //找到后继节点赋值给返回变量 25 returnValue = parent; 26 } 27 } 28 29 return returnValue; 30 } 31 /** 32 *在以root为根节点中找出节点值为value的后继节点方法 33 */ 34 TNode<T>* TreeSuccessor(const T &value,TNode<T> *returnValue){ 35 return TreeSuccessor(root,value,returnValue); 36 }
如下图:
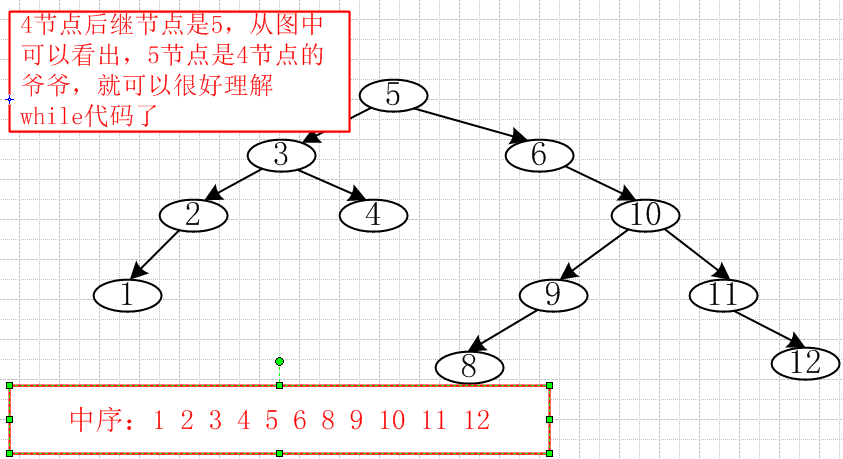
10、先序、中序、后序递归和非的递归遍历,更详细的请参考上一篇文章,为什么在这里有展示一遍,我坚信在复杂的东西,多动手写几次都能很好的理解
1 /** 2 *前序非递归(利用栈)遍历二叉树 3 *前序遍历的规则:根左右 4 *非递归遍历树会经常当做面试题,考察面试者的编程能力 5 *防止下次被鄙视,应该深入理解并且动手在纸写出来 6 */ 7 void PreOrderTraverse() { 8 //申明一个栈对象 9 stack<TNode<T>*> s; 10 //t首先指向根节点 11 TNode<T> *t = root; 12 //压入一个空指针,作为判断条件 13 s.push(0); 14 15 //如果t所值节点非空 16 while (t != 0) { 17 //直接访问根节点 18 std::cout << (&t->data) << " "; 19 20 //右孩子指针为非空 21 if (t->rchild != 0) { 22 //入栈右孩子指针 23 s.push(t->rchild); 24 } 25 26 //左孩子指针为非空 27 if (t->lchild != 0) { 28 //直接指向其左孩子 29 t = t->lchild; 30 } else {//左孩子指针为空 31 //获取栈顶元素(右孩子指针) 32 t = s.top(); 33 //清楚栈顶元素 34 s.pop(); 35 } 36 37 } 38 } 39 40 /** 41 *中序非递归(利用栈)遍历二叉树 42 *前序遍历的规则:左根右 43 */ 44 void InOrderTraverse() { 45 //申明一个栈对象 46 stack<TNode<T>*> s; 47 //t首先指向根节点 48 TNode<T>* t = root; 49 50 //节点不为空或者栈对象不为空,都进入循环 51 while (t != 0 || !s.empty()) { 52 //如果t节点非空 53 if (t) { 54 //入栈t节点 55 s.push(t); 56 //t节点指向其左孩子 57 t = t->lchild; 58 } else { 59 //获取栈顶元素(左孩子指针) 60 t = s.top(); 61 //清楚栈顶元素 62 s.pop(); 63 //直接访问t节点 64 std::cout << (&t->data) << " "; 65 //t节点指向其右孩子 66 t = t->rchild; 67 } 68 } 69 } 70 /** 71 *后序非递归(利用栈)遍历二叉树 72 *前序遍历的规则:左右根 73 */ 74 void PostOrderTraverse() { 75 //申明一个栈对象 76 stack<TNode<T>*> s; 77 //t首先指向根节点 78 TNode<T>* t = root; 79 //申请中间变量,用做判断标识 80 TNode<T>* r; 81 //节点不为空或者栈对象不为空,都进入循环 82 while (t != 0 || !s.empty()) { 83 //如果t节点非空 84 if (t) { 85 //入栈t节点 86 s.push(t); 87 //t节点指向其左孩子 88 t = t->lchild; 89 } else { 90 //获取栈顶元素(左孩子指针) 91 t = s.top(); 92 //判断t的右子树是否存在并且没有访问过 93 if (t->rchild && t->rchild != r) { 94 //t节点指向其右孩子 95 t = t->rchild; 96 //入栈t节点 97 s.push(t); 98 //t节点指向其左孩子 99 t = t->lchild; 100 } else { 101 //获取栈顶元素(左孩子指针) 102 t = s.top(); 103 //清楚栈顶元素 104 s.pop(); 105 //直接访问t节点 106 std::cout << (&t->data) << " "; 107 //设置已经访问过的节点,防止多次访问(右孩子指针) 108 r = t; 109 t = 0; 110 } 111 } 112 } 113 } 114 /** 115 * 根据模式递归遍历二叉树 116 * 下面代码相对比较简单,只要记住遍历树的规则并且弄一点递归,都可以写出来 117 * 如果在面试中实在写不出来非递归方式,可以写一个递归版本,也许可以争取一个好的工作 118 */ 119 void OrderTraverse(const TNode<T>* t, Style mode) { 120 if (t) { 121 //先序遍历二叉树:根左右 122 if (mode == Pre) { 123 //直接访问t节点 124 std::cout << (&t->data) << " "; 125 //递归遍历左子树 126 this->OrderTraverse(t->lchild, mode); 127 //递归遍历右子树 128 this->OrderTraverse(t->rchild, mode); 129 } 130 //中序遍历二叉树:左根右 131 if (mode == In) { 132 //递归遍历左子树 133 this->OrderTraverse(t->lchild, mode); 134 //直接访问t节点 135 std::cout << (&t->data) << " "; 136 //递归遍历右子树 137 this->OrderTraverse(t->rchild, mode); 138 } 139 //后序遍历二叉树:左右根 140 if (mode == Post) { 141 //递归遍历左子树 142 this->OrderTraverse(t->lchild, mode); 143 //递归遍历右子树 144 this->OrderTraverse(t->rchild, mode); 145 //直接访问t节点 146 std::cout << (&t->data) << " "; 147 } 148 } 149 }
11、按层级遍历树
1 /** 2 *按层级从左到右遍历树 3 */ 4 void LevelOrderTraverse(){ 5 //声明一个队列队形 6 queue<TNode<T>* > q; 7 //声明变量a,t;并把root赋值给t 8 TNode<T> *a,*t = root; 9 //若t节点非空 10 if(t){ 11 //t节点入队列 12 q.push(t); 13 //如果队列不为空 14 while(!q.empty()){ 15 //获取队列头结点 16 a = q.front(); 17 //数据队形出队列 18 q.pop(); 19 //直接访问队列头结点值 20 std::cout<<a->data<<" "; 21 //若a节点左子树不为空 22 if(a->lchild){ 23 //左子树入队列q 24 q.push(a->lchild); 25 } 26 //若a节点右子树不为空 27 if(a->rchild){ 28 //右子树入队列q 29 q.push(a->rchild); 30 } 31 } 32 } 33 }
12、运行结果,由于在虚拟机中打中文,实在太痛苦,弄一点英文装下B
测试代码如下:
 View Code
View Code
结果如下图

11、完整代码
TNode.h
 View Code
View Code
BSTree.h
 View Code
View Code
五:环境
1、运行环境:Ubuntu 10.04 LTS+VMware8.0.4+gcc4.4.3;
2、开发工具:Eclipse+make
六:题记
1、上面的代码难免有bug,如果你发现代码写的有问题,请你帮忙指出,让我们一起进步,让代码变的更漂亮和更健壮;
2、我自己能手动写上面代码,离不开郝斌、高一凡、侯捷、严蔚敏等老师的书籍和视频指导,在这里感谢他们;
3、鼓励自己能坚持把更多数据结构方面的知识写出来,让自己掌握更深刻,也顺便冒充下"小牛";
4、所有动画都在网上找的,感谢制作做动画的朋友,这样好的动画比图片更便于大家理解复杂的内容;
欢迎继续阅读“启迪思维:数据结构和算法”系列
