【算法剖析】求字符串中无重复字符的最长字串

【算法剖析】求字符串中无重复字符的最长字串

1、问题描述

　　这个问题来自leetcode中的Longest Substring Without Repeating Characters，诚如标题所述，我们需要寻找的是在一个字符串中，没有重复字符的最长字串。我们假定字符串中的字符只由a~z这26个字符构成。例如，对于字符串"abcabcbb"，它的无重复字符最长字串是"abc"，长度为3；对于字符串"bbbb"，它的无重复最长字串是b，长度为1。

2、算法一

　　我们能够立即想到的，最原始的算法就是，从字符串的每一个位置开始构造字串，并逐渐增大字串长度，直到碰到一个已经出现在这个字串中的字符为止，这样对于长度为n的字符串而言，经过n次遍历即可求得最长的无重复字符字串。实际上，考虑到构成字符串的字母表大小只有26，每次遍历最多也只需进行26次增长子串的操作，这个算法的整个时间复杂度为O(26n)。这个算法很简单也很好理解，不再给出详细代码。

3、算法二

　　算法二能够将时间复杂度缩小到O(n)，即只遍历一遍字符串即可。它主要基于一个思想：当我们在构建子串的时候，如果遇到了一个重复字符，那么我们可以使遍历跳跃一定“距离”，直接忽略掉不必要的搜索。对于一个字符串A=a0a1a2a3...an−1，我们正在构造的字串是B=ajaj+1...ak，接下来一个字符是ak+1，但是它与当前B中的某一字符ak′相同。那么对于那些所有以ai,(j+1≤i<k)开头的无重复字符最长字串的长度一定小于B的长度。例如，对于字符串A="abcdcef"，B="abcd"，当前长度为4，下一个字符是c，而它与b3相同，那么在A中，以a1,a2,a3开头的无重复字符最长字串，相对于B，“更早地”遇到了重复字符c，它们的长度都要小于B的长度。

　　为了实现算法二，我们需要额外使用一个大小为26的数组pos以及一个变量basePos，pos用来记录当前情况下，每个字符最近出现的那个位置，而basePos用来记录所增长的子串的开始位置。初始情况下，basePos=0，表示第一个所增长的那个子串开始于位置0，pos中的每个元素都初始为-1。对于当前的字串，我们如何判断下一个字符是否已经出现在了当前字串中呢？例如，对于字符a，我们检查pos[0]≤basePos是否成立，成立的话，则说明a已经出现在当前字串中，弄明白需要搞清楚pos与basePos的含义。

　　我们使用一个例子来说明这个过程。

---

初始情况

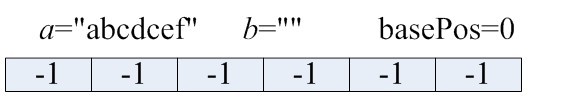
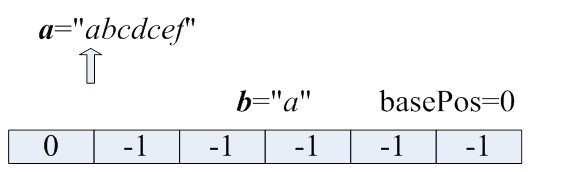
Step：1

Step：2

Step：3

Step：4

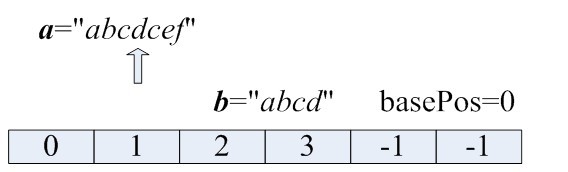
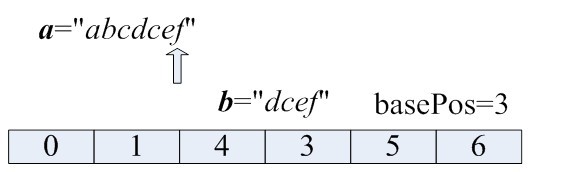
Step：5

注意，这里是由于pos['c'-'a']=2>basePos，也就是第二个c与前面的c重复了。

Step：6

Step：7

---

下面我们给出代码，我们需要处理某些特殊情况，例如输入字符串为空串等等。

 

 int lengthOfLongestSubstring(string s) {
        int pos[26];
        int i;
        
        for(i=0;i<26;i++)
        {
            pos[i]=-1;
        }
        int basePos=0;
        int maxLength=-1;
        for(i=0;i<s.length();i++)
        {
            if(pos[s[i]-'a']<basePos)
            {
                pos[s[i]-'a']=i;
            }
            else 
            {
                if(maxLength==-1||i-basePos>maxLength)
                    maxLength=i-basePos;
                basePos=pos[s[i]-'a']+1;
                pos[s[i]-'a']=i;
            }
        }
        if(s.length()-basePos>maxLength||maxLength==-1) maxLength=s.length()-basePos;
        return maxLength;
    }

作者：Chenny Chen 
出处：http://www.cnblogs.com/XjChenny/ 
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

 

 

标签: 数据结构, 算法, 经典算法, 面试题, Longest Substring Without Repeating Characters