维特比算法和隐马尔可夫模型的解码
一、概述
维特比算法是安德鲁.维特比(Andrew Viterbi)于1967年为解决通信领域中的解码问题而提出的,它同样广泛用于解决自然语言处理中的解码问题,隐马尔可夫模型的解码是其中典型的代表。无论是通信中的解码问题还是自然语言处理中的解码问题,本质上都是要在一个篱笆网络中寻找得到一条最优路径。
所谓篱笆网络,指的是单向无环图,呈层级连接,各层节点数可以不同。如图是一个篱笆网络,连线上的数字是节点间概念上的距离(如间距、代价、概率等),现要找到一条从起始点到终点的最优路径。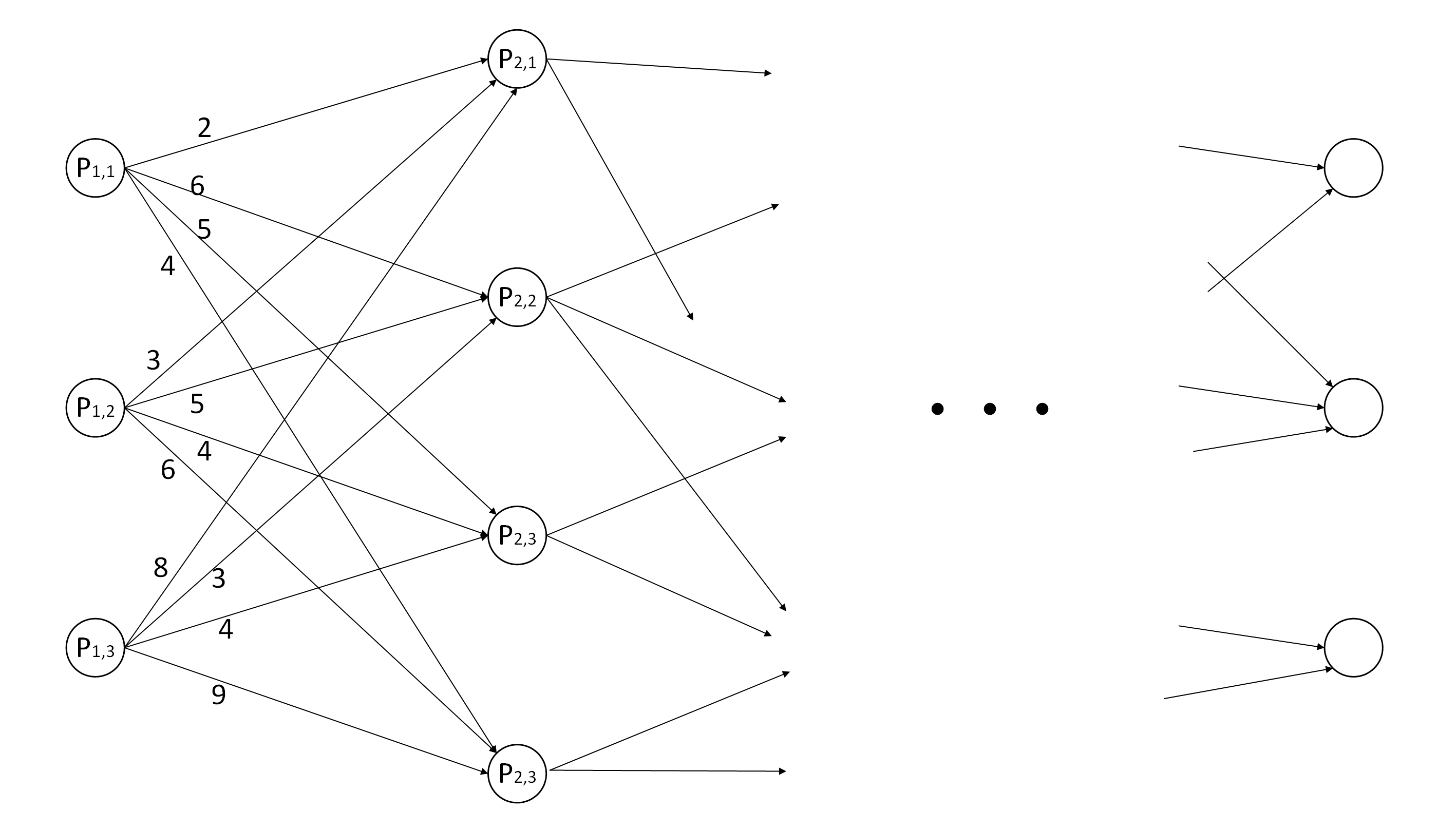
在实际问题中,节点数和层数往往是大量的,因而采取遍历所有的路径计算其距离进行比较的方式是不可行的。维特比算法正是通过动态规划的方式高效求得这条最优路径。
二、维特比算法
1.算法原理
该问题具有这样一个特性,对于最优(如最短距离)的路径,任意一段子路径一定是该段两端点间所有可达路径中最优的,如若不然,将该段中更优的子路径接到两端点便构成了另一个整体最优路径,这是矛盾的。或者说,最优路径中,从起始点到由近及远的任一点的子路径,一定是该段所有可达路径中最优的。也即,整体最优,局部一定最优。
该特性也就是说,对每个节点而言,如果最优路径经过这一点,则一定是经过从起始点到这点的这段最优路径。那么,只要从头开始,由局部向整体推进,渐次地找到起始点到当前点的最优路径,算至终点便得到了整体最优路径。这样的方式叫做动态规划,是维特比算法的基本思想。
维特比算法求解篱笆网络最短路径的过程为:
从第一层开始,对每一层的每一个节点,计算出起始点到它的最短距离,并记录下相应最短路径下它的前一个节点,逐层递推,算至终止点时便得到了整体最短距离,再依照节点记录下的前置节点进行回溯,就得到了最短路径的序列。对第ii层第jj个节点Pi,jPi,j,假设起始点到它的最短距离为D(Pi,j)D(Pi,j),相应最短路径下它的前一个节点为Pre(Pi,j)Pre(Pi,j),则
也就是,对前一层的所有节点,计算每一个节点的记录的最短距离D与它到当前节点的距离d的和,取其中最小的那个值(其中, d(A,B)d(A,B)表示A,B两节点间的距离。).
也就是,满足距离最短的那条路径上在前一层的节点.
2.示例
在如下网络中,连线上的数字是节点间的距离,求S点到E点的最短距离和与之对应的路径。
第一层:
对节点P1,1P1,1,
起始点到它只有一条路径,最短距离D(P1,1)=2D(P1,1)=2,前一个节点Pre(P1,1)=SPre(P1,1)=S;
对节点P1,2P1,2,
起始点到它只有一条路径,最短距离 D(P1,2)=1D(P1,2)=1,前一个节点Pre(P1,2)=SPre(P1,2)=S;
对节点P1,3P1,3,
起始点到它只有一条路径,最短距离D(P1,3)=3D(P1,3)=3,前一个节点Pre(P1,3)=SPre(P1,3)=S 。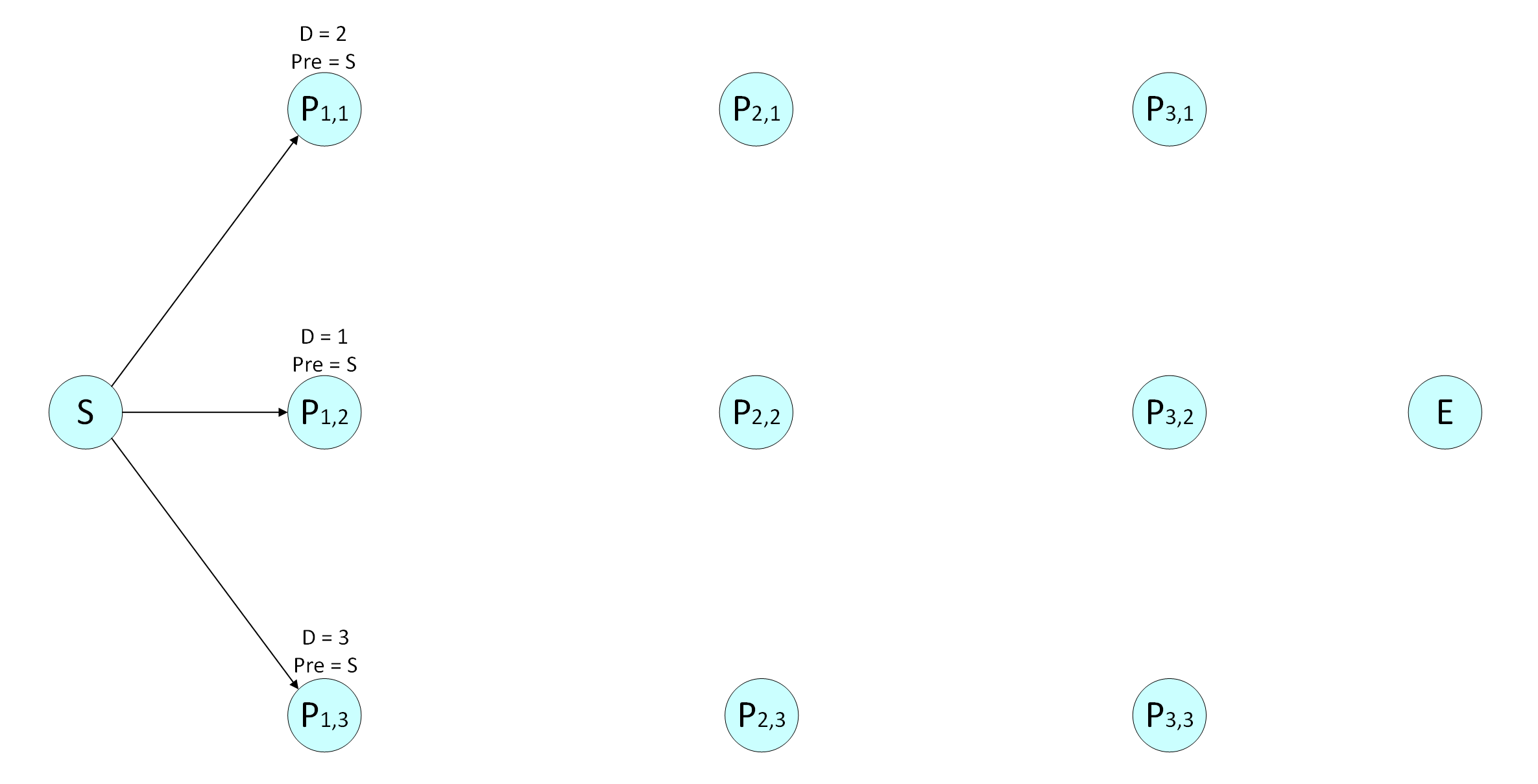
第二层:
对节点 P2,1P2,1,
D(P1,1)+d(P1,1,P2,1)=2+3=5D(P1,1)+d(P1,1,P2,1)=2+3=5,
D(P1,2)+d(P1,2,P2,1)=1+2=3D(P1,2)+d(P1,2,P2,1)=1+2=3 ,
D(P1,3)+d(P1,3,P2,1)=3+9=12D(P1,3)+d(P1,3,P2,1)=3+9=12,
最短距离 D(P2,1)=min{5,3,12}=3D(P2,1)=min{5,3,12}=3,前一个节点Pre(P2,1)=P1,2Pre(P2,1)=P1,2 ;
对节点P2,2P2,2 ,
D(P1,1)+d(P1,1,P2,2)=2+6=8D(P1,1)+d(P1,1,P2,2)=2+6=8,
D(P1,2)+d(P1,2,P2,2)=1+5=6D(P1,2)+d(P1,2,P2,2)=1+5=6,
D(P1,3)+d(P1,3,P2,2)=3+2=5D(P1,3)+d(P1,3,P2,2)=3+2=5,
最短距离D(P2,2)=min{8,6,5}=5D(P2,2)=min{8,6,5}=5,前一个节点Pre(P2,2)=P1,3Pre(P2,2)=P1,3 ;
对节点P2,3P2,3,
D(P1,1)+d(P1,1,P2,3)=2+4=6D(P1,1)+d(P1,1,P2,3)=2+4=6 ,
D(P1,2)+d(P1,2,P2,3)=1+7=8D(P1,2)+d(P1,2,P2,3)=1+7=8,
D(P1,3)+d(P1,3,P2,3)=3+6=9D(P1,3)+d(P1,3,P2,3)=3+6=9 ,
最短距离D(P2,3)=min{6,8,9}=6D(P2,3)=min{6,8,9}=6,前一个节点Pre(P2,3)=P1,1Pre(P2,3)=P1,1 ;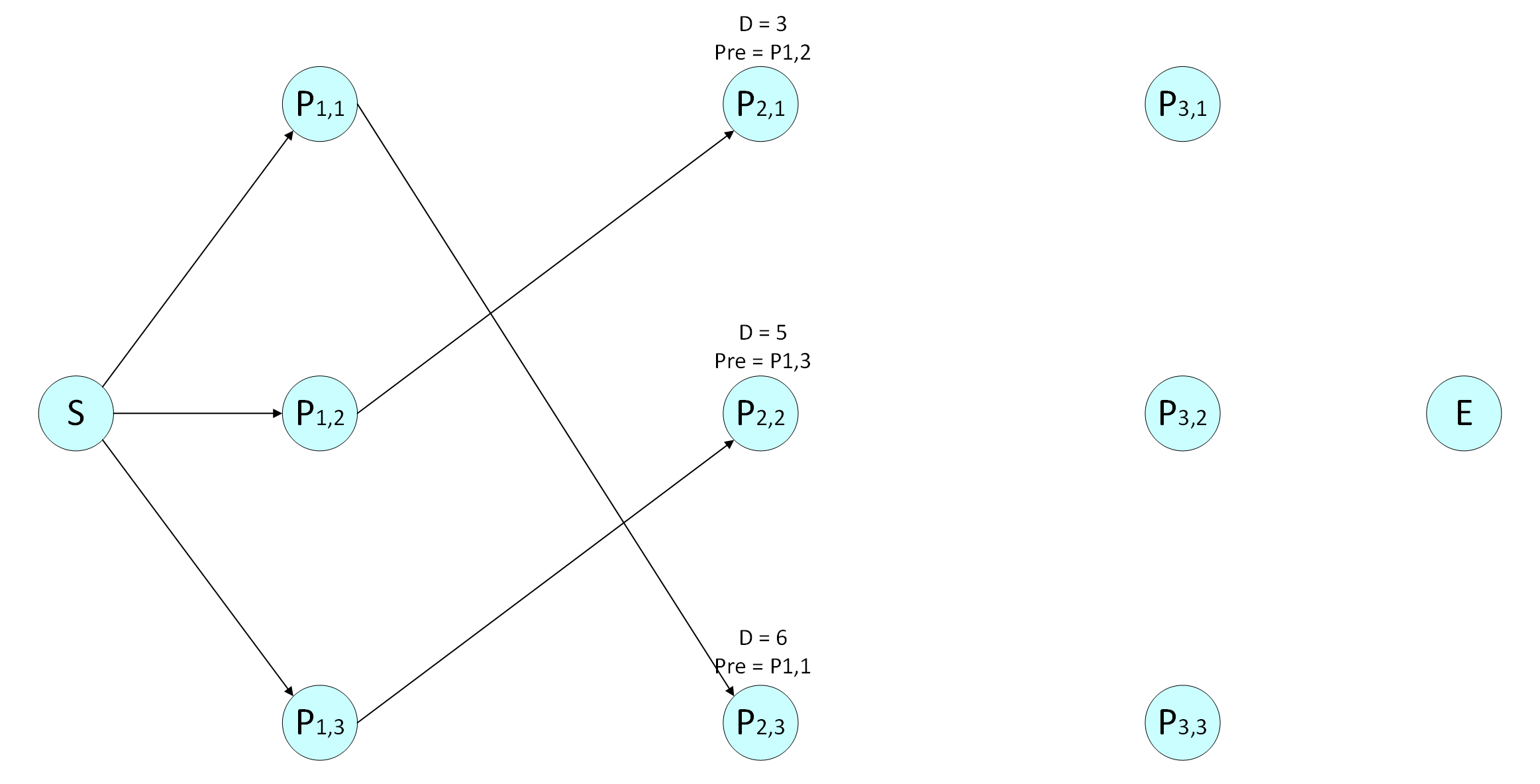
第三层:
对节点 P3,1P3,1,
D(P2,1)+d(P2,1,P3,1)=3+9=12D(P2,1)+d(P2,1,P3,1)=3+9=12,
D(P2,2)+d(P2,2,P3,1)=5+2=7D(P2,2)+d(P2,2,P3,1)=5+2=7,
D(P2,3)+d(P2,3,P3,1)=6+6=12D(P2,3)+d(P2,3,P3,1)=6+6=12,
最短距离D(P3,1)=min{12,7,12}=7D(P3,1)=min{12,7,12}=7,前一个节点Pre(P3,1)=P2,2Pre(P3,1)=P2,2;
对节点P3,2P3,2,
D(P2,1)+d(P2,1,P3,2)=3+3=6D(P2,1)+d(P2,1,P3,2)=3+3=6,
D(P2,2)+d(P2,2,P3,2)=5+6=11D(P2,2)+d(P2,2,P3,2)=5+6=11,
D(P2,3)+d(P2,3,P3,2)=6+3=9D(P2,3)+d(P2,3,P3,2)=6+3=9,
最短距离D(P3,2)=min{6,11,9}=6D(P3,2)=min{6,11,9}=6,前一个节点Pre(P3,2)=P2,1Pre(P3,2)=P2,1;
对节点P3,3P3,3,
D(P2,1)+d(P2,1,P3,3)=3+8=11D(P2,1)+d(P2,1,P3,3)=3+8=11,
D(P2,2)+d(P2,2,P3,3)=5+7=12D(P2,2)+d(P2,2,P3,3)=5+7=12,
D(P2,3)+d(P2,3,P3,3)=6+4=10D(P2,3)+d(P2,3,P3,3)=6+4=10,
最短距离D(P3,3)=min{11,12,10}=10D(P3,3)=min{11,12,10}=10,前一个节点Pre(P3,3)=P2,3Pre(P3,3)=P2,3;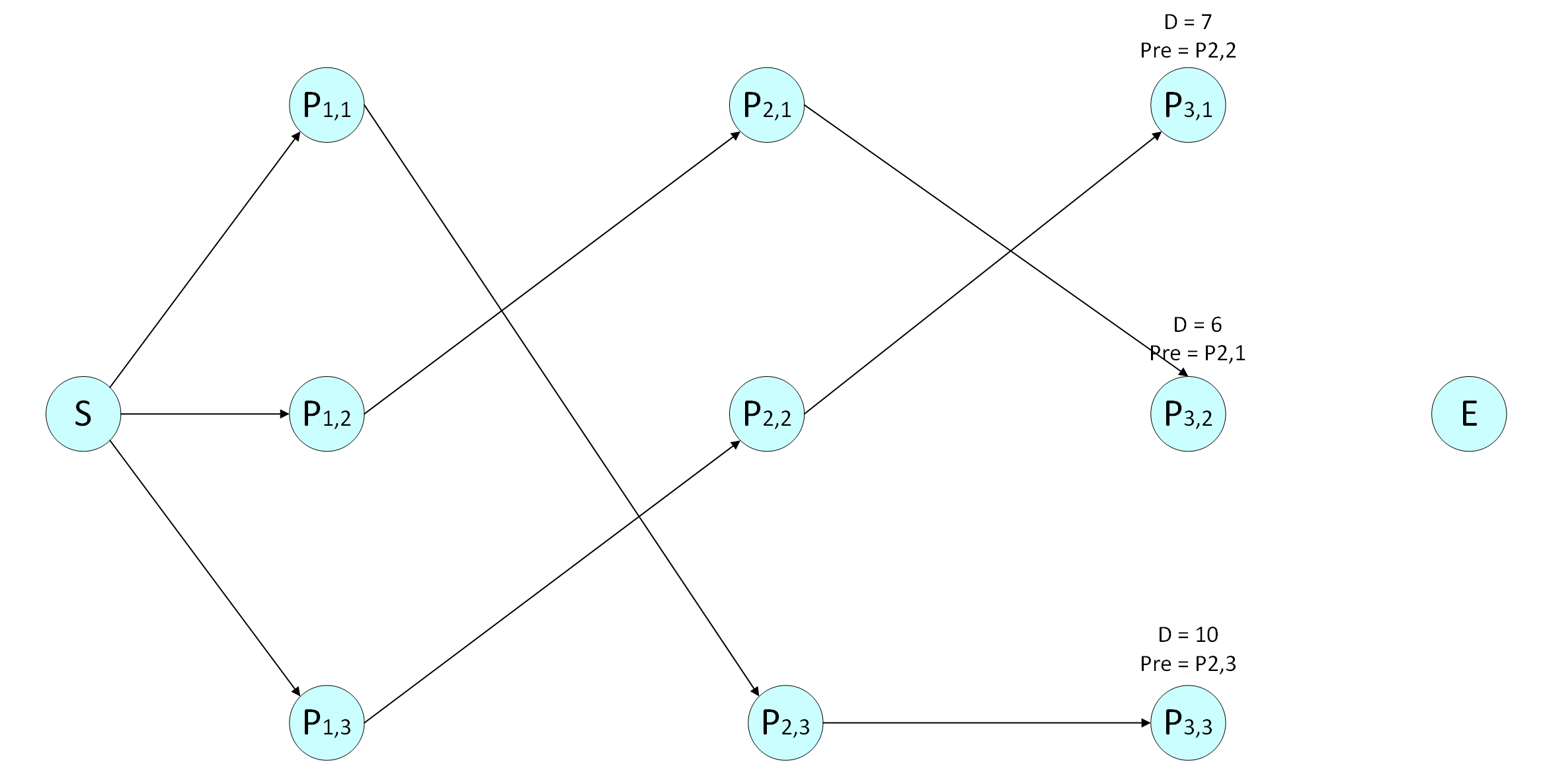
第四层(终点):
对节点 EE,
D(P3,1)+d(P3,1,E)=7+3=10D(P3,1)+d(P3,1,E)=7+3=10,
D(P3,2)+d(P3,2,E)=6+7=13D(P3,2)+d(P3,2,E)=6+7=13,
D(P3,3)+d(P3,3,E)=10+6=16D(P3,3)+d(P3,3,E)=10+6=16,
最短距离D(E)=min{10,13,16}=10D(E)=min{10,13,16}=10,前一个节点Pre(E)=P3,1Pre(E)=P3,1;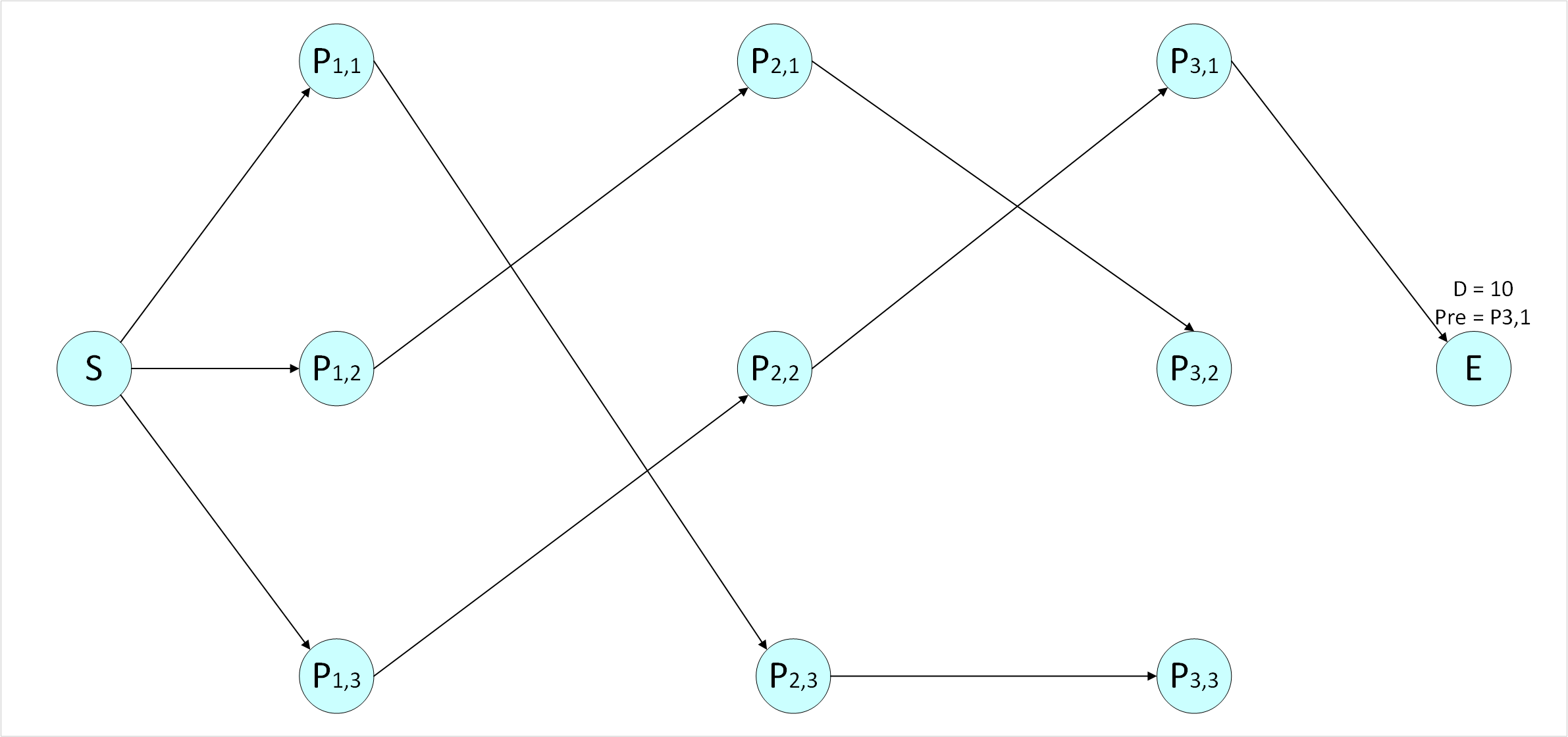
又Pre(E)=P3,1Pre(E)=P3,1,Pre(P3,1)=P2,2Pre(P3,1)=P2,2,Pre(P2,2)=P1,3Pre(P2,2)=P1,3,Pre(P1,3)=SPre(P1,3)=S
故最短距离为10,与之对应的路径为(SS,P1,3P1,3,P2,2P2,2,P3,1P3,1,EE).
三、隐马尔可夫模型的解码
1.问题描述
隐马尔可夫模型(HMM)的解码问题指,给定模型和输出序列,如何找出最有可能产生这个输出的状态序列。自然语言处理中,也即如何通过观测信号确定最有可能对应的实际语义。在状态序列上,每个状态位是状态集合中的元素之一,因此该问题等价于在状态集合中的节点构成的有向网络(篱笆网络)中找出一条概率最大的路径(最优路径),如图。该问题可以通过维特比算法得到高效的解决。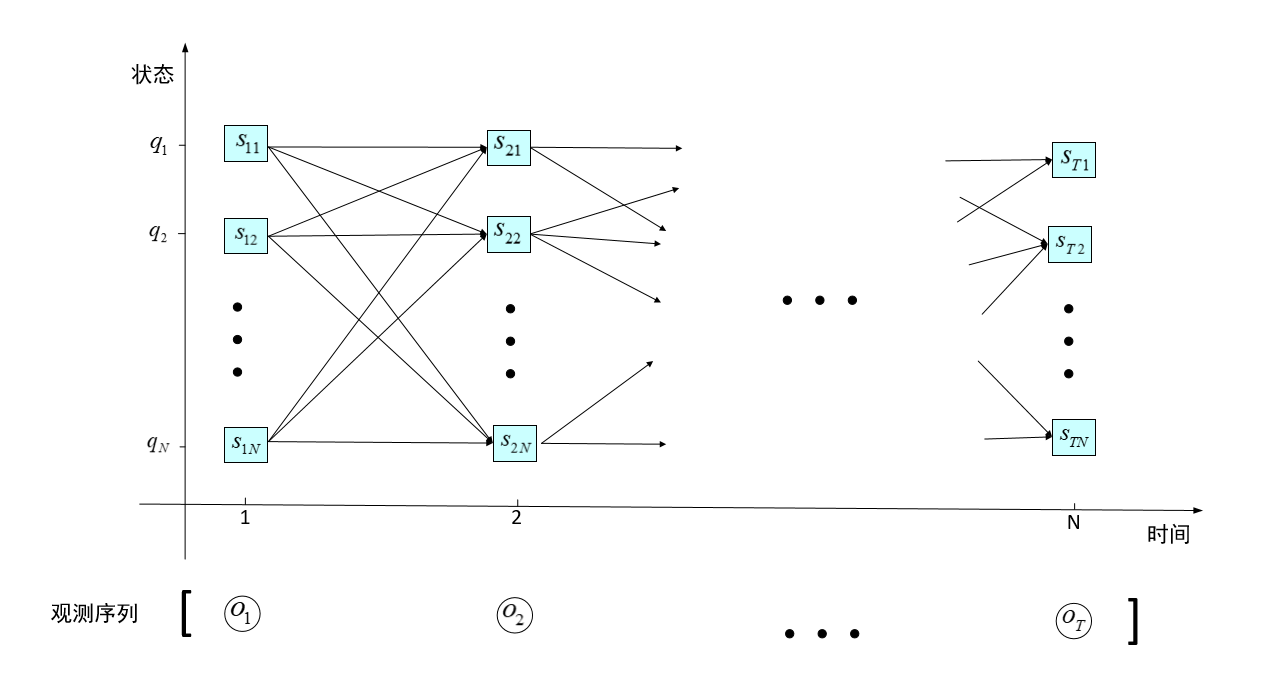
2.算法叙述
假设 P(st,j)P(st,j)表示从起始时刻到st,jst,j的最优路径的概率,Pre(st,j)Pre(st,j)表示从起始时刻到 st,jst,j的最优路径上前一个节点,则隐马尔可夫模型的维特比解码算法为:
输入:隐马尔可夫模型 λ=(π,A,B)λ=(π,A,B)和观测 O=(o1,o2,...,oT)O=(o1,o2,...,oT);
输出:最优状态序列S∗=(s∗1,s∗2,...,s∗T)S∗=(s1∗,s2∗,...,sT∗).
(1)初始化
P(s1,j)=πjbj(o1)P(s1,j)=πjbj(o1),
Pre(s1,j)=NonePre(s1,j)=None,j=1,2,...,Nj=1,2,...,N
(2)递推
对 t=2,3,...,Tt=2,3,...,T
,j=1,2,...,Nj=1,2,...,N.
(3)递推终止
最大概率
最优路径上的最后一个状态
(4)回溯路径,确定最优状态序列
S∗=(s∗1,s∗2,...,s∗T−1,s∗T)S∗=(s1∗,s2∗,...,sT−1∗,sT∗)
=(Pre(s∗2),Pre(s∗3),...,Pre(s∗T),s∗T)=(Pre(s2∗),Pre(s3∗),...,Pre(sT∗),sT∗)
3.示例
(参考自《统计学习方法》)
状态集合 Q={q1,q2,q3}Q={q1,q2,q3},观测集合V={0,1}V={0,1},模型 λ=(π,A,B)λ=(π,A,B) ,
A=⎡⎣⎢0.50.30.20.20.50.30.30.20.5⎤⎦⎥A=[0.50.20.30.30.50.20.20.30.5] , B=⎡⎣⎢0.50.40.70.50.60.3⎤⎦⎥B=[0.50.50.40.60.70.3],π=(0.2,0.4,0.4)Tπ=(0.2,0.4,0.4)T
已知观测序列O=(0,1,0)O=(0,1,0),求最优状态序列。
解:
(1)在t=1时(初始化),对每一个状态,求观测为0的最大概率
P(s1,1)=0.2×0.5=0.1P(s1,1)=0.2×0.5=0.1,Pre(s1,1)=NonePre(s1,1)=None
P(s1,2)=0.4×0.4=0.16P(s1,2)=0.4×0.4=0.16,Pre(s1,2)=NonePre(s1,2)=None
P(s1,3)=0.4×0.7=0.28P(s1,3)=0.4×0.7=0.28,Pre(s1,3)=NonePre(s1,3)=None
(2)在t=2时,对每一个状态,求观测为1的
最大概率
当前最优的前一个状态
P(s2,1)=max{0.1×0.5×0.5,0.16×0.3×0.5,0.28×0.2×0.5}P(s2,1)=max{0.1×0.5×0.5,0.16×0.3×0.5,0.28×0.2×0.5}=0.028=0.028
Pre(s2,1)=s1,3=q3Pre(s2,1)=s1,3=q3
P(s2,2)=max{0.1×0.2×0.6,0.16×0.5×0.6,0.28×0.3×0.6}P(s2,2)=max{0.1×0.2×0.6,0.16×0.5×0.6,0.28×0.3×0.6}=0.0504=0.0504
Pre(s2,2)=s1,3=q3Pre(s2,2)=s1,3=q3
P(s2,3)=max{0.1×0.3×0.3,0.16×0.2×0.3,0.28×0.5×0.3}P(s2,3)=max{0.1×0.3×0.3,0.16×0.2×0.3,0.28×0.5×0.3}=0.042=0.042
Pre(s2,3)=s1,3=q3Pre(s2,3)=s1,3=q3
(3)在t=3时,对每一个状态,求观测为0的
最大概率
当前最优的前一个状态
P(s3,1)=max{0.028×0.5×0.5,0.0504×0.3×0.5,0.042×0.2×0.5}P(s3,1)=max{0.028×0.5×0.5,0.0504×0.3×0.5,0.042×0.2×0.5}=0.00756=0.00756
Pre(s3,1)=s2,2=q2Pre(s3,1)=s2,2=q2
P(s3,2)=max{0.028×0.2×0.4,0.0504×0.5×0.4,0.042×0.3×0.4}P(s3,2)=max{0.028×0.2×0.4,0.0504×0.5×0.4,0.042×0.3×0.4}=0.01008=0.01008
Pre(s3,2)=s2,2=q2Pre(s3,2)=s2,2=q2
P(s3,3)=max{0.028×0.3×0.7,0.0504×0.2×0.7,0.042×0.5×0.7}P(s3,3)=max{0.028×0.3×0.7,0.0504×0.2×0.7,0.042×0.5×0.7}=0.0147=0.0147
Pre(s3,3)=s2,3=q3Pre(s3,3)=s2,3=q3
(4)得到结果.
最大概率
P∗=max1≤j≤3P(s3,j)P∗=max1≤j≤3P(s3,j)
=max{0.00756,0.01008,0.0147}=max{0.00756,0.01008,0.0147}
=0.0147=0.0147
最优状态序列
S∗=(Pre(s∗2)t,Pre(s∗3),s∗3)S∗=(Pre(s2∗)t,Pre(s3∗),s3∗)
=(s1,3,s2,3,s3,3)=(s1,3,s2,3,s3,3)
=(q3,q3,q3)=(q3,q3,q3)
4.python实现
对上述HMM解码示例的python实现程序为
import numpy as np
def viterbi(pi, A, B, Q, V, obs_seq):
'''
:param pi:HMM初始状态概率向量,list类型
:param A:HMM状态转移概率矩阵,list类型
:param B:HMM观测生成概率矩阵,list类型
:param Q:状态集合,list类型
:param V:观测集合,list类型
:param obs_seq:观测序列,list类型
:return:最优状态序列的概率sta_pro,float类型;最优状态序列sta_seq,list类型
'''
# HMM模型参数转换为array类型
pi = np.array(pi)
A = np.array(A)
B = np.array(B)
# 1.定义动态计算结果存储矩阵
rowNum = len(Q) # 行数,状态数
colNum = len(obs_seq) # 列数,生成的观测数,即时刻数
# 存储节点当前最大概率的矩阵
probaMatrix = np.zeros((rowNum,colNum))
# 存储当前最优路径下的前一个节点的矩阵
preNodeMatrix = np.zeros((rowNum,colNum))
# 2.初始化(第1时刻)
probaMatrix[:,0] = pi*np.transpose(B[:,obs_seq[0]])
preNodeMatrix[:,0] = [-1]*rowNum # 第1时刻节点的前一个节点不存在,置为-1
# 3.递推,第2时刻至最后
for t in range(1, colNum):
list_pre_max_proba = [] # 节点最大前置概率列表
list_pre_node = [] # 节点当前最优路径中前一个节点列表
for j in range(rowNum):
pre_proba_list = list(np.array(probaMatrix[:,t-1])*np.transpose(A[:,j])) # 前置概率列表,前一时刻的节点最大概率与到当前节点转移概率的乘积
'''
注:因为计算机的二进制机制对小数的表达是有限的,所以对小数作运算将产生一定的误差。
在使用函数获取pre_proba_list中的最大值和对应的索引时,为有效降低这种误差,将数据放大后再进行操作。
'''
pre_proba_list = [x*pow(10,5) for x in pre_proba_list] # 放大100000倍
prePro = max(pre_proba_list)/pow(10,5) # 最大前置概率
preNodeIndexNum = pre_proba_list.index(max(pre_proba_list)) # 前置节点的索引号
list_pre_max_proba.append(prePro) # 最大前置概率加入列表
list_pre_node.append(preNodeIndexNum) # 前置节点的索引号加入列表
probaMatrix[:,t] = np.array(list_pre_max_proba)*np.transpose(B[:,obs_seq[t]]) # 最大前置概率乘上观测概率,即为当前最大概率
preNodeMatrix[:,t] = list_pre_node # 将该列前置节点索引号加入矩阵
# 此时,得到了完整的probaMatrix和preNodeMatrix,对这两个矩阵进行操作便可得到需要的结果
# 4.得到最大概率
maxPro = np.max(probaMatrix[:, colNum-1]) # 全局最大概率(即最后一列的最大值)
# 5.得到最优状态序列的状态索引号列表
lastStateIndexNum = np.argmax(probaMatrix[:, colNum-1]) # 最优状态序列中最后一个状态的索引号
stateIndexList = [] # 定义最优状态的索引号列表
stateIndexList.append(lastStateIndexNum)
# 回溯,完成状态索引号列表
currentIndex = lastStateIndexNum;
for t in range(colNum-1, 0, -1):
fls = preNodeMatrix[:, t].tolist() # 矩阵中的数值是浮点型
ls = list(map(int, fls)) # 转为整型
currentIndex = ls[currentIndex]
stateIndexList.append(currentIndex)
stateIndexList.reverse() # 反转列表
# 6.由索引号序列得到最优状态序列
stateSeq = [Q[i] for i in stateIndexList]
return maxPro,stateSeq
if __name__=='__main__':
# 状态集合
Q = ["q1", "q2", "q3"]
# 观测集合
V = [0, 1]
# 初始状态概率向量
pi = [0.2, 0.4, 0.4]
# 状态转移概率矩阵
A = [[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]]
# 观测概率矩阵
B = [[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]]
# 观测序列
obs_seq = [0, 1, 0]
maxPro, stateSeq = viterbi(pi, A, B, Q, V, obs_seq)
print("最大概率为:", maxPro)
print("最优状态序列为:", stateSeq)

End.
参考
- 吴军. 数学之美(第二版). 人民邮电出版社.
- 李航. 统计学习方法. 清华大学出版社.
- https://www.cnblogs.com/zhibei/p/9391014.html