可落地的DDD(5)-战术设计
摘要
本篇是DDD的战术篇,也就是关于领域事件、领域对象、聚合根、实体、值对象的讨论。也是DDD系列的完结篇。
这一部分在我们团队争论最多的,也有很多月经贴,比如对资源库的操作应该放在领域服务还是领域对象中。
聚合根应不应该暴露给外部,还是要转成DTO。这些问题我们讨论了大半年,最后大家基本达成了共识,在当前的业务规模下,
这些问题没那么重要,可东可西。不会对代码的质量有啥大的影响。关于DDD的实践,与团队的水平、业务复杂度息息相关。我们的经验并不一定就适用你们团队。我将战术篇的这么多的内容放在了一篇文章中,并且大部分都是引用之前的讨论、总结。
原因还是在于我内心深处并没有觉得战术篇的实践给我们团队带来多么大的改变。战略篇的是我认为更重要的。
DDD系列文章断断续续也有十来篇了,主要是总结我们团队落地过程遇到的问题和解决方案,算是DDD从学习到落地实践的一个完整的闭环链路,希望对你有所启发。当然这个过程受益最大的肯定是我本人。系统性的思考问题、总结问题、阐述问题是非常有助于提升个人思维能力,朋友们你们也可以尝试一下。
建模
DDD的出现,是大家对于事务性编程,面向数据库表编程的一个反思,明明软件设计是一个面向对象的设计,需要考虑对象之间的继承、多态、组合。
为什么到实际编码过程中成了过程性的编程,为什么对象只有属性没有方法了,也就是失血模型。
关于这几种编程的详细介绍可以参考Martin的《Patterns of Enterprise Application Architecture》Page110
所以我个人觉得,DDD的作用有两个,一个是面向业务的,帮助分析业务模型,进行业务建模。另外一个是面向解决域,即代码落地。
即使用一个规范能够反映对象之间的关系,即OO编程。
目前对DDD研究主要有以下类别
- 关于业务分析层面,如何进行概念层面的抽象和设计的方法论
- 关于服务划分、代码分层、职责定义的方法论
- DDD框架的讨论,比如jdon
第3点基本上没怎么广泛的讨论。我认为未来也不会出现什么牛逼的DDD框架能够流行起来。DDD是一种建模方法,是针对不同的业务领域的,
在不同的团队有不同的落地方案,是没办法靠一种框架来约束,来把一件不统一的事情来统一起来。就好比我们面向对象的设计针对问题域,抽象出来了
20多种设计模式。这些设计模式都是指导思想,你不能搞出一种框架,来约束大家使用某种设计模式就基于这种框架扩展,以此来达到代码统一或者降低
编程难度的目的。
前面的文章主要是比较大的方面,比较适合做整体业务分析。也就是第一个点。今天主要讨论第二点。
OO 编程
DDD的代码分层、职责定义本质上就是OO编程。OO的三大基本要素就是继承、多态、组合。这三个是深度抽象的结果。没法指导具体的编程。
于是我们有了设计模式,前辈们针对问题域,总结除了24种设计模式,这样遇到类似的问题时,我们可以使用对应的设计模式去解决问题。
而这些设计模式底层使用到还是继承、多态、组合。
那有了设计模式了,为什么还要DDD呢?为什么很少看到开源软件用DDD呢?
个人的理解DDD还是面向企业应用架构的,是在众多不确定的业务,系统中提炼出来的一套规范,这样必然是高度抽象的。而开源软件大多是领域比较确定的,比如数据库领域,中间件领域。解决这类问题的系统架构通常会更加复杂以及具有扩展性。
DDD的工程架构网上有很多,我在之前的文章也提到过,这里不再赘述,看下老马的这个,我觉得非常清晰的展现出来了职责分离
https://martinfowler.com/articles/microservice-testing/#conclusion-summary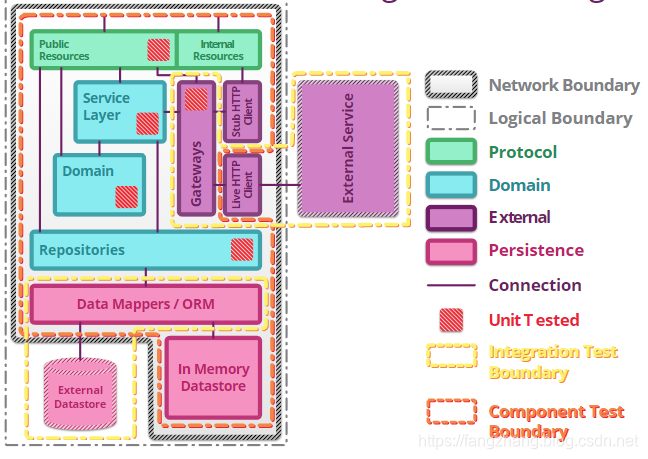
我们重点看领域一层。
领域包含3点
领域服务
领域对象
领域事件
基础设施层
为各层提供资源服务(如数据库、缓存等),实现各层的解耦,降低外部资源变化对业务逻辑的影响。
总结
-
DDD中国
http://ddd-china.com/look-back-2017.html 视频去网站看 -
美团的实践
https://tech.meituan.com/2017/12/22/ddd-in-practice.html -
cnblog博客园有很多.net DDD实践的文章
https://www.cnblogs.com/zhili/category/603514.html
http://www.cnblogs.com/daxnet/archive/2012/12/27/2836372.html -
jdon上面的系列
https://www.jdon.com/ddd.html -
框架方面(个人觉得没啥用,参考看看)
rafy框架:http://zgynhqf.github.io/Rafy/articles/%E9%A2%86%E5%9F%9F%E5%AE%9E%E4%BD%93%E6%A1%86%E6%9E%B6.html
-
一些相关的书籍pdf上传到百度网盘,需要的自取。
链接: https://pan.baidu.com/s/1kGYk1dHbTAjBS4kd9s1VWw
提取码: 36w4
