卡方检验(Chi_square_test)： 原理及python实现

概述

• What for？主要用在某个变量(或特征)值是不是和应变量有显著关系，换种说法就是看某个变量是否独立
• (X^2=sum{frac{(observed-expected)^2}{expected}})
  observed表示观测值,expected为理论值，可以看出,理论值与观测值差别越大,(X^2)越大

Contingency table(联连表)

介绍卡方检验之前，需要先介绍下联连表,因为这个是所有假设检验的基础,这个直接看中文翻译容易不知所以，个人认为维基百科上解释的比较到位：是一种矩阵形式的表格,用来表示变量或者多变量的频率分布。
似乎意思知道了一点，我们现在举个例子：

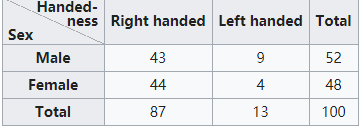
一目了然。

实现过程

然后我们看下实现过程：
1 按照假设检验的步骤，首先我们需要确定原假设(H_0)(null hypothesis):原假设是变量独立的，实际观测频率和理论频率一致。
2 其次我们根据实际观测的联连表，去求理论的联连表；(卡方统计值：X^2)，记为Statistic；自由度，
3 然后选取适合的置信度(一般为95%)同自由度一起确定临界值Critical Value，比较卡方统计值和临界值大小：

• If Statistic >= Critical Value: 认为变量对结果有影响，则拒绝原假设，变量不独立
• If Statistic < Critical Value: 认为变量对结果没有影响，接受原假设，变量独立

python 中用scipy.stats 中chi2_contingency实现：

from scipy.stats import chi2_contingency
from scipy.stats import chi2

table = [[10,20,30],[6,9,17]]
print(table)
stat,p,dof,expected = chi2_contingency(table) # stat卡方统计值，p：P_value，dof 自由度，expected理论频率分布
print('dof=%d'%dof)
print(expected)

prob = 0.95 # 选取95%置信度
critical = chi2.ppf(prob,dof)  # 计算临界阀值
print('probality=%.3f,critical=%.3f,stat=%.3f '%(prob,critical,stat))
if abs(stat)>=critical:
    print('reject H0:Dependent')
else:
    print('fail to reject H0:Independent')

显示结果：
probality=0.950,critical=5.991,stat=0.272 
fail to reject H0:Independent

除了直接比较(X^2)和临界值外，

我们还可以比较p-value和显著性水平(significance level),alpha:

• P_value<=alpha:认为有显著性影响,则拒绝原假设,变量不独立
• P_value>alpha:认为没有显著性影响,则接受原假设,变量独立

python实现

# interpret p_value
alpha = 1-prob
print('significance=%.3f,p=%.3f'%(alpha,p))
if p<alpha:
    print('reject H0:Dependent')
else:
    print('fail to reject H0:Independent')

显示结果：
significance=0.050,p=0.873
fail to reject H0:Independent

reference：
https://en.wikipedia.org/wiki/Contingency_table
https://www.jianshu.com/p/807b2c2bfd9b
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html
https://machinelearningmastery.com/chi-squared-test-for-machine-learning/