摘自:http://blog.csdn.net/abcjennifer/article/details/7748833
===============================
回忆传统压缩
对于原始信号x∈C(N*1),传统压缩是构造正交矩阵D∈C(N*N),正变换为y=Dx, 反变换x=D-1y= DTy, D-1= DT。
将初始信号x变换到y∈C(N*1)后,将保留其中的K个分量(K人工指定),对其他N-K个分量置零,这样的信号y就称为K稀疏(K-Sparse)的。于是得到编码策略如下:
- Code(编码):构造正交矩阵D,做正变换y=Dx, 保留y中最重要的K个分量及其对应位置。
- Decode(解码):将K个分量及其对应位置归位,其他位置置零,得到y,构造D,并用x=D-1y恢复x。
换句话说,传统压缩就是构造正交阵进行编解码,将所有N维信号全部存储下来。其弊端是,
- 1. 由于香农定理的限制,采样频率很大,这样造成了原始信号很长(N很大),消耗时间和空间。
- 2. K个重要分量要分别存储其位置,多分配空间。
- 3. K中分量(在传输过程中)丢失的话不好恢复。
[ S-sparse ]:A model case occurs when x is known to be S-sparse for some 1≤S≤n, which means that at most S of the coefficients of x can be non-zero.
===============================
压缩感知概念 & 线性度量
卍 压缩感知初识:
与传统压缩不同的是,压缩感知采用的y=Dx中,D不是N*N, 而是D∈C(M*N)的,其中M<N,也就是说D是一个扁矩阵,未知数个数大于方程个数。对于方程Dx=y, x∈C(N*1),y∈C(M*1),
我们知道,当M>=N的时候,这是一个determined或over-determined的problem,而且容易求解;而M<N的时候问题是under-determined的,如果我们假设x是稀疏的,最好的solution就是能够满足Ax≈b的最稀疏的x。CS惊人之处就是可以解决这种under-determined的问题:给定M*1的y,可以根据D恢复出N*1的x, 其中M<<N。如果x是S稀疏(S-sparse)的(或者想要让它是S稀疏的),那么我们只需要取那S个度量(from N个未知量x)就好了。
卍 线性度量:
对于上面的问题y=Dx, 当M<N时我们已知有无穷多解。假设x0是其中一个特解的话,那么通解形式即为x0+WZ,其中W∈C(N*(N-M)),是D的零空间的一组基,Z是这组基的线性组合,总有DWZ=0。所以我们的任务就是找x0+WZ中最稀疏的解x(为什么找最稀疏的后面会有证明的定理)。
这里,原先传统压缩中N*N的D越冗余,其零空间越大,寻找更稀疏矩阵的选择越多(即x0+WZ越多)。
卍 求解问题:

[example of CS-imaging]:(from ppt of 陶哲轩)
A typical example of when this assumption is reasonable is in imaging. An image may consist of ∼106 pixels and
thus require a vector of n∼106 to fully represent. But, if expressed in a suitable wavelet basis, and the image does
not contain much noise or texture, only a small fraction (e.g. 104) of the wavelet coefficients should be significant.
(This is the basis behind several image compression algorithms, e.g. JPEG2000.)
Intuitively, an S-sparse vector x has only S degrees of freedom, and so one should now be able to reconstruct x using only S or so measurements.This is the philosophy of compressed sensing(or compressive sensing, or compressive sampling): the number of measurements needed to accurately capture an object should be comparable to its compressed size, not its uncompressed size.
===============================
压缩感知适合解决什么问题?
卍 信号是稀疏的
卍 sensor方计算代价较大,receiver方计算代价较小(即不适合将信息全部存储下来,而适合取少量信息,之后恢复)

===============================
压缩感知是否可行?
说起这个问题可能有人会奇怪,什么叫是否可行呢?就是说给出D和M维的y,是否可以唯一地把x恢复出来?答案是肯定的!
Compressive Sensing中有两个问题,对于![]()
- 一个是怎样确定出一个stable的基Θ,或者测量矩阵Φ
- 另一个是如何进行信号x的恢复(下一小节)

[ S-sparse ]:A model case occurs when x is known to be S-sparse for some 1≤S≤n, which means that at most S of the coefficients of x can be non-zero.
定理:假设Ax=b中,A是m*n的矩阵,x是n维向量,y是m维向量,A中任意2S列都是线性无关的(即无法线性组合得到0向量),则s-sparse的向量x可以被b和A唯一地重构出来,i.e.

证明:假设可以重建出两个向量x,x'同时满足Ax=Ax'=b,其中x和x'都是S-Sparse的;那么就有A(x-x')=0; 因为x-x'中非零元素个数<=2S,所以x-x'是2S-Sparse的,又因为给出条件A中任意2S个列向量都是线性独立(线性无关)的,这就与A(x-x')=0矛盾了,所以假设不成立,即,可以根据b和A唯一地恢复出x∈C(n*1)。
===============================
怎样恢复原信号?
我们已知所选择的最稀疏的x即x中非零元素最少的,即x的零范数最小的(向量的零范数即为其稀疏度sparsity)。然而,求x=argmin||x||0使得x满足Ax=b的一个子问题是一个NP完全问题,需要在S个compoments中选出1,2,...,n个,看能从中选出最少多少个,满足Ax=b,这样,对于每一个n都有排列组合C(S,n)种方法,显然不可行。所以我们想能不能换个什么方法来恢复信号,自然而然的,我们想到了最小平方法。具体见下图Fig B。

Fig A. 用二范数代替零范数
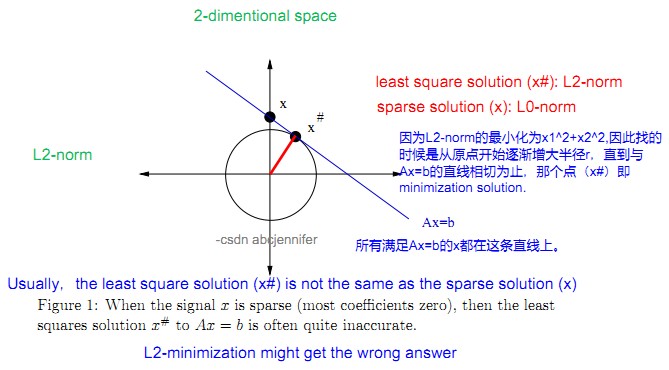
Fig B. L2范数下寻找满足Ax=b的x,发现有一定偏差。
symmerize:
2-methods to methods:
1. L2-norm: quick, efficient, but get the wrong answer
2. L0-norm: precise but impractical
否定了L0范数和L2范数之后,我们想到取中——用L1范数(Basis pursuit的思路)。
so get select the L1-norm , that is the abs of each element
===============================
Basis Pursuit & RIP

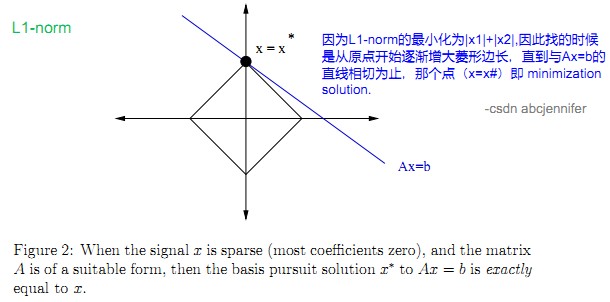
从图中可见,L1-norm比L2-norm靠谱多了。从上图中可见,x*处,x的L1-norm最小,这样推广到n维向量x,就是其每一维的值的绝对值的和。
下面这个Theorem就是对L1-norm方案(Basis pursuit)可行性的定理(具体证明看论文吧):大概是说,原始S-sparse的信号f为n维,从其中随机抽取m维分量,如果想利用Basis pursuit的方法把这m维向量重建出n维原始信号,只要满足m>cS*log(n)即可,其中c是一个常数。

很多实验结果表明呢,大多数S-sparse信号 f 可以在m>=4*S的时候得以很好的重建,由此有了下面更强的RIP假设:
假设A中任意4S列都是几乎正交的,i.e. 在这4S列中,前4S个奇异值都在[0.9,1,1]范围内,则任意S-sparse信号x可以通过basis pursuit 由 Ax重建。

2006年,Tao和Donoho的弟子Candes合作证明了在RIP条件下,0范数优化问题与以下1范数优化问题具有相同的解

上面已经说过一个定理:对于Ax=b,A中任意2S列都线性独立,则任意S-sparse的向量x都可以被恢复出来,这是理论上的说法。实际上,利用basis pursuit进行恢复时需要增强条件:A中的每4S列都是几乎正交的。这个精确的条件就是RIP,许多matrix都服从这个条件。
补充:

实际上以上的1范数优化问题是一个凸优化,故而必然有唯一解,至此sparse representation的大坑初步成型。总结一下:
- 如果矩阵满足sparsity=2S,则0范数优化问题有唯一解。
- 进一步如果矩阵A满足RIP条件,则0范数优化问题和1范数优化问题的解一致。
- 1范数优化问题是凸优化,故其唯一解即为0范数优化问题的唯一解。
===============================
噪声
实际应用中,我们用b=Ax+z来进行拟合,对付噪声的干扰,其中z是高斯噪声向量。

Fig. Reconstructing a sparse signal x approximately from noisy data b=Ax+z, assuming that z has norm less than error tolerance e.
===============================
CS应用——single pixel camera
Rice大学首先研究出的单像素相机是CS的一个主要应用。

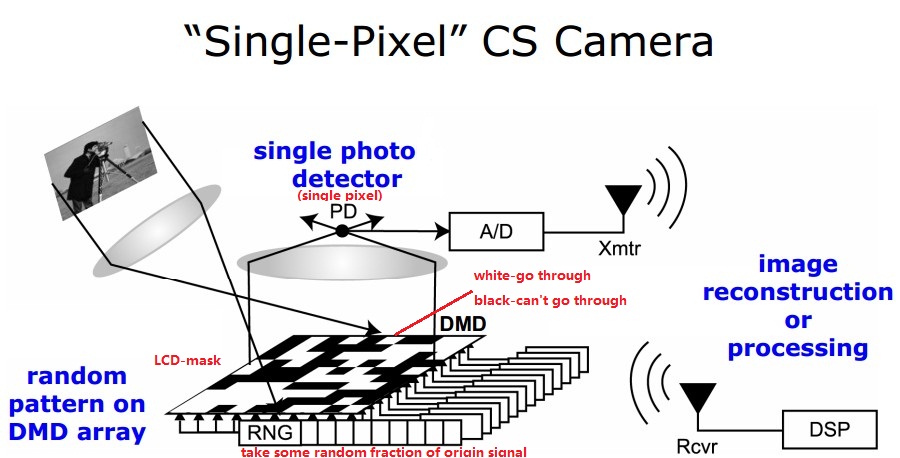


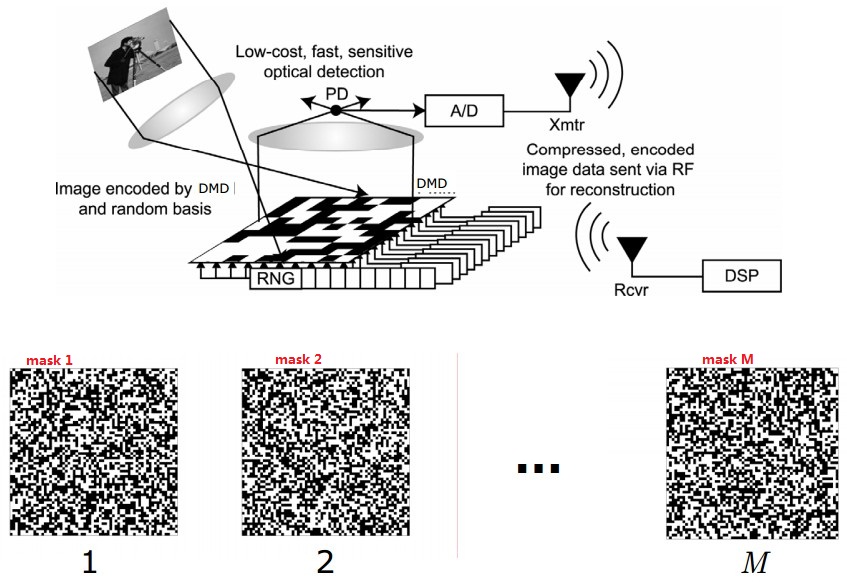

test image(65536 pixels ) and CS construction using 11000 and 1300 measurements