让我们开始吧。
我就不举例了,主要给自己理解而且没人看,懒得再加例子了。我也不用术语了,理由同上。我自己也整不明白啥事神经网络的反向传播,我是玻璃心,我很菜但你不能骂我呜呜呜(逃
我们的目标是什么?找到一个“权值”,使得神经网络——这里用“全相联”——输出的东西尽可能准确。什么是准确?我们没办法找到一个完美的表达式,只能找到一个近似的“函数”——在这里是神经网络——来尽可能输入一个x,然后获得一个尽可能准确的y。为了构造这么一个“函数”,我们需要一些数据。
我们的数据都是类似((x),(y))这样的“对”,我们有很多这样的“对”。我们想办法找到一个函数,这个函数拥有这样的性质:输入我们的“数据集”里面的x们,输出的y们尽可能和我们本来就有的y相同。(We want to find out a function that has these properties: for the input in our dataset, the output should be correspond to our original output or lable)
“输出的y们尽可能和我们本来就有的y相同”,这句话里面的“尽可能”我们怎么定义?我们用一个函数:
(cost(mathbf{X}, mathbf{Y}, Theta)=-frac{1}{m}left[sum_{i=1}^{m}left(mathbf{logleft(h_{Theta}left(x^{(i)}
ight)
ight)}mathbf{y^{(i)}}^T+ mathbf{log left(1-h_{Theta}left(x^{(i)}
ight)
ight)}left(mathbf{1-y^{(i)}}
ight)^T
ight)
ight])
这个是挺不符合常用惯例的,反正也没人看我就这么用了怎么滴(逃
其中,(mathbf{X})是我们数据集的输入部分,一行一个“数据例子”,我们有“m”行,第 i 行——我们叫做(mathbf{x^{(i)}})——都是一个“数据例子”,一行里面有a个“数据特征”。
(mathbf{Y})是我们数据集的“预期输出部分”——也就是我们想要的输出——一样的,我们有“m”行。一行一个“数据例子的输出”,第 i 行——我们叫做(mathbf{y^{(i)}})——是数据例子的输出,一行有b个“结果显示”。
(mathbf{h_{Theta}(x^{(i)})})就是我们的神经网络了,详情请参阅下图:

g(x)就是sigmoid这个激活函数。
我们没有考虑正则化这些压着过拟合的东西。
注意那一整坨东西都是在累加符号——(Sigma)——里面的。什么?你说哪一坨?你觉得哪坨恶心那就是哪一坨(逃
这个函数可能和一些别的书不同,这个意会就好。
前置知识如上。还有就是梯度下降了。
我们正式开始。
回到我们的评判标准——也就是(cost(mathbf{X}, mathbf{Y}, Theta)),容易知道,越大,那么结果偏离的越大。我们想办法把这玩意尽可能变小,两种方法:直接算极值或者借助借助梯度下降。我们用梯度下降这种方法来演示。梯度下降是啥?逆着梯度往下走——我们使用全部的数据,不搞任何优化。
我们就用演示神经网络那张图里面的神经网络,来演示反向传播。
大家凑合着看吧,这个文字编辑器我不会用,只好用这份手稿了。
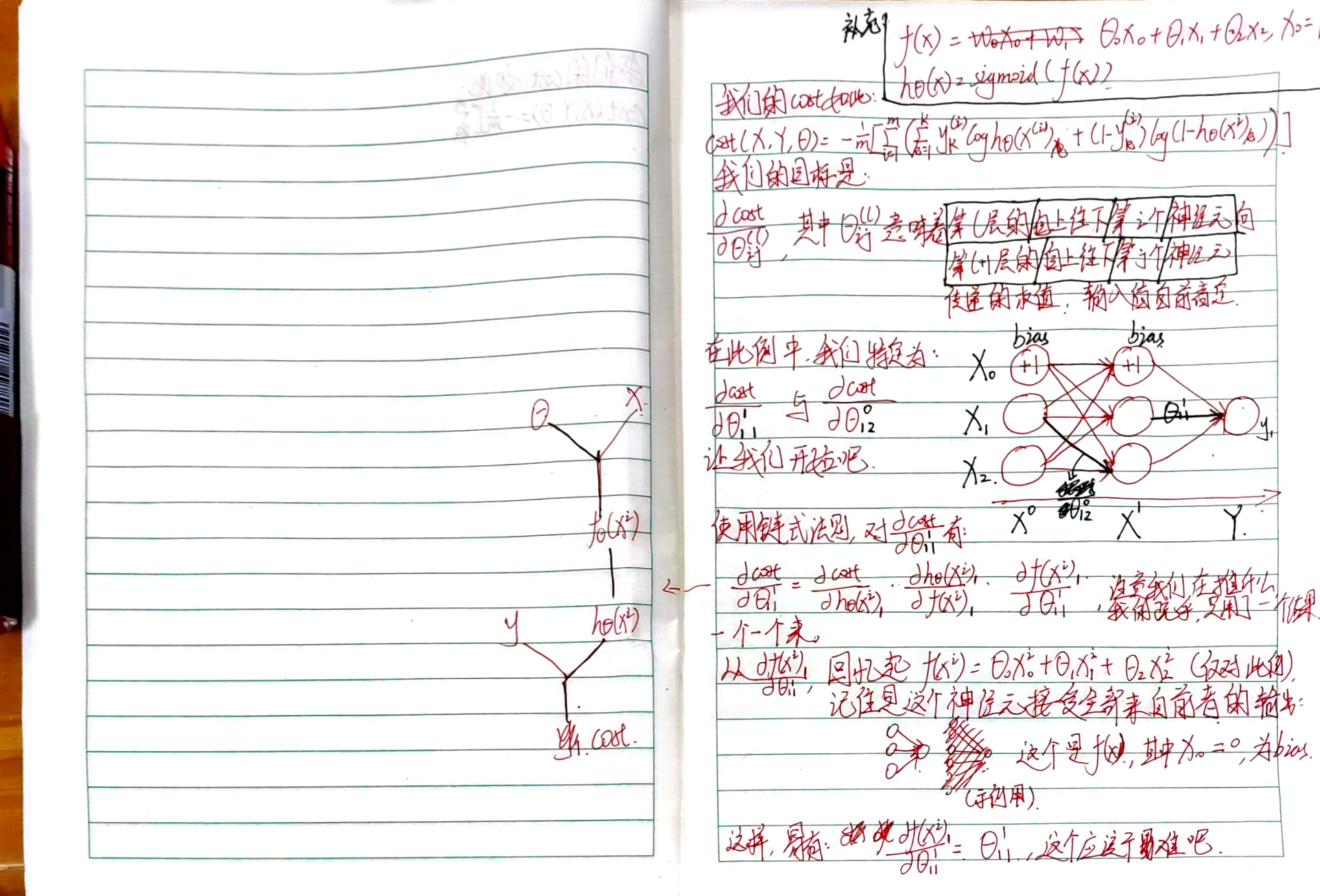


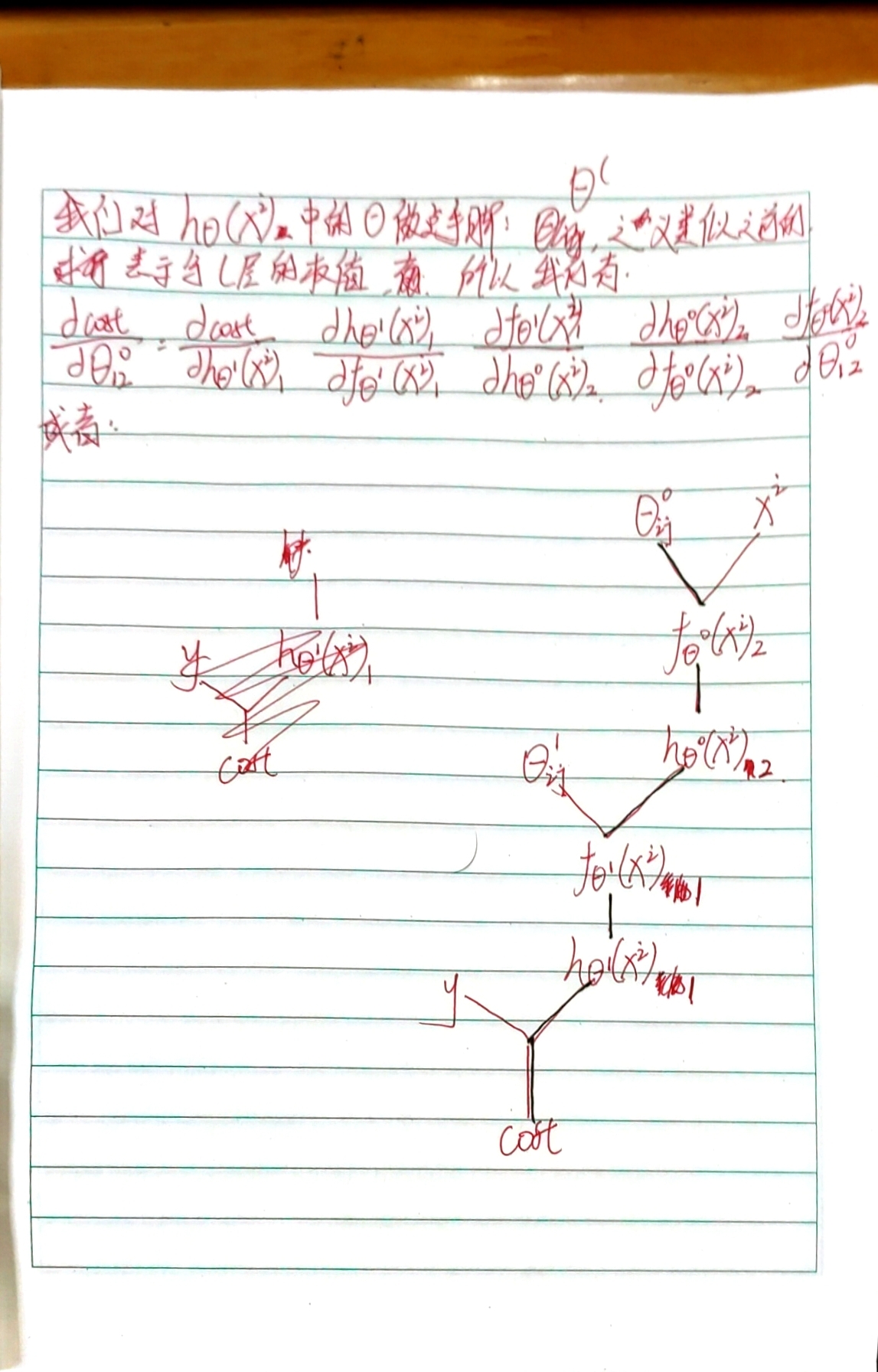
大家看的时候不要嫌弃我就好(逃