我发现 写博客真的会上瘾
刚好下周要考集图了,在博客上把知识点都梳理一遍好了。
一、集合论
1.2 命题逻辑
命题:能够判断真假的陈述句。
原子命题:不包含其他命题作为其组成部分的命题。
复合命题:5种联结词将原子命题联结起来的命题

1.3 一阶谓词逻辑
原子命题的划分:划分个体性质的原子命题
划分个体之间关系原子命题
原子命题=主语+谓语=个体+谓词
谓词:表示个体性质或彼此之间关系的词
量词:表示数量的词
全称量词&存在量词
等值式基本可以推,但有几个需要记住。

前范束式:把 和
和 提前。
提前。
1.4集合的概念
子集的等价:(证明中常用)


幂集:设A为一个集合,称由A的全体子集组成的集合为A的幂集,记作P(A),P(A)={X|X包含于A}
集族与指标集:
1.5 集合的运算
对称差:
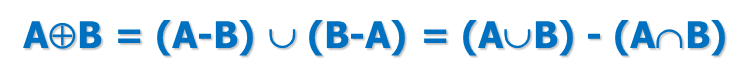
广义并:集族的广义并是指其全体元素(集合)的元素组成的集合。


同理,广义交:集族的广义交就是全体元素(集合)的公共元素组成的集合,就是每个子集合的大交。
容斥原理:

1.6 集合恒等式
基本上是转换成谓词恒等式的证明题。注意包含的证法。
2.1 有序对和卡式积
有序对:{{a},{a,b}}为元素a,b构成的有序对,记作<a,b>
卡式积:
非结合、非交换、有分配律
2.2 二元关系
n元关系:元素是有序n元组的集合。
<x,y> 属于 某二元关系f,则称x与y具有f关系
A到B的二元关系f:f包含于AXB。f是AXB的子集。
二元关系f定义域和值域的定义:存在y/x使得<x,y>属于f的x/y集合。
逆的定义;
合成的定义;
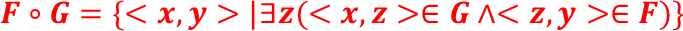
合成有结合律,对并、逆有分配律。
二元关系f在集合A上的限制:x属于集合A的且本身属于f的二元有序对的集合。
集合A在二元关系f中的象:二元关系f在集合A上的限制的值域。
二元关系是单根的定义:对于任意一个属于值域的y,在二元关系f定义中仅存在一个x,使<x.y>属于f。单值类似。
2.3关系的表示和性质
在集合A上的二元关系f的关系矩阵;关系矩阵的乘法与合成关系;可达矩阵;
集合A上的二元关系f的有向图;
二元关系的性质:
自反性:在A上的二元关系,对任意属于A的元素x,<x,x>都属于f,否则是非自反。
反自反:在A上的二元关系,对任意属于A的元素x,<x,x>都不属于f,否则是非反自反
非反自反=非自反
对称性:在A上的二元关系,对任意属于A的元素x,y,若<x,y>属于f,则<y,x>也属于f
反对称:在A上的二元关系,对任意属于A的元素x,y,若<x,y>属于f,则<y,x>不属于 f,除非x=y;
可同时具有对称性和反对称性。
传递性:在A上的二元关系,对任意属于A的元素x,y,z,若<x,y>,<y,z>属于f,那么 <x,z>也属于f。
2.4关系的幂运算和闭包
二元关系R的闭包:本身具有(自反/对称/传递)的性质的二元关系
二元关系R包含于这个二元关系
对于其他的有这些性质的(自反/对称/传递)的二元关系R‘,如果R包含于R’, 则R的闭包也包含于R‘。即R的闭包是最小的,具有这些性质(自反/对称/ 传递)且包含R的二元关系。
闭包的求法:自反闭包直接并上IA
对称闭包并上自身的逆
传递闭包并上二次可达,三次可达....直到成为传递闭包为止
证明R自反:证明IA包含于R
证明R对称:证明R的逆=R
证明R传递:证明R和R的复合包含于R
r(R)=IaU R
s(R)=R-1UR
t(R)=R U R2 U R3....
2.5等价关系和划分
等价关系:R是自反的、对称的和传递的二元关系
二元等价关系上的等价类:设R为A上的等价关系,对于任意的x属于A,在R上x(把它看成单元集 合)的象,称为x关于R的等价类。
由等价关系,等价类中元素的等价类都是一样的。
商集:等价类的集合,R是定义在A上的二元关系,R是等价的,对任意的x属于A,都对应着一个等价类,这些等价类的集合就是A关于R的商集,等于说R把A分成了许多等价类。
划分:划分是一个集族,它包含于A的幂集,就是说它的每一个元素都是A的子集。商集就是一个划 分。
还需要满足,空集不是它的元素
它的元素不相交
大并集为A
同块关系:同块关系是定义在A上的关于某划分A一个二元关系,若<x,y>属于同块关系,那么x,y必 须同属于划分A的某一个元素。同块关系是一个等价关系。
Stiring 子集数:把n元集分成K个非空子集的分法数
(n,0)=0;(n,1)=1;(n,2)=2^(n-1)-1 先放一个球,区分两个子集,然后n-1个球有2^(n-1)种放法,最后减去全部球都在一个子集里的方法。
(n,k)=k*(n-1,k)+(n-1,k-1);放最后一个球的时候有两种情况,K个子集都有球了,所以有K种放法;只有K-1个子集有球,最后一个球占一个子集。
一个集合A上有多少种等价关系=A上有多少种划分(分成一个非空子集、两个、三个...一直到|A|个。
加细:两个划分之间的比较。
2.6序关系
偏序关系:定义在集合A上的二元关系R,若R是自反的,反对称的,传递的,则R为A上的偏序关系。
偏序集:R是A上的偏序关系,则二元有序对<A,R>为偏序集。
可比:x,y属于A,只要x,y同属于R种某一个二元有序对,则X,Y可比。
严格小于:当<x,y>属于偏序关系R,且x!=y,那么x严格小于y
覆盖:x严格小于y,且不存在一个z,使得x严格小于z,z严格小于y。
哈斯图:用顶点表示A种元素,仅当y覆盖x时,将y画在x上方并连线。
全序关系:如果一个偏序关系R,A中任意的元素x,y均可比,则R就升级为全序关系,偏序集<A,R>就升级为全序集。
拟序关系:定义在集合A上的二元关系R,若R是反自反、(反对称)、传递的,在R为A上的拟序关系。(反自反性和传递性可推出反对称性)。<A,R>为拟序关系。
拟全序关系:如果一个拟序关系R,A中任意元素x,y均可比(x!=y)或者x=y时,或者可以用三歧性来表示(<x,y><y,x>,x=y三式有且只有一个成立),此时逆序关系就升级为拟全序关系,<A,R>升级为拟全序集。
最大元最小元:B包含于A,y属于B,若y是B的最大元,那么对于任意属于B的元素x,都有<x,y>属于某偏序关系R。(他比别的都大)若y是B的最小元,那么<y,x>属于R。
极大元极小元:若y是B的极大元,对于任意属于B且<y,x>属于R的元素x,x=y,这样就放松了对y的限制,y不需要与任意x均可比了。(没有比他大的)
上界下界:y是B的上界,那么对任意x属于B,<x,y>属于偏序关系R。
最小上界最大下界:上界的最小元和下界的最大元
链:B包含于A,B如果是A中的链,任意的x,y属于B,x与y均可比;
如果B是A中的反链,任意不想等的x,y属于B,x与y均不可比;
A中最长链(长度为n),一定存在极大元。对A来说,A存在n个划分块,使得每个划分块都是反链。
|A|=mn+1,那么A中要么存在m+1的反链,要么存在n+1的链。
良序:对全序关系或者拟全序关系,如果对于A中任意一个非空子集B,B均有最小元,那么这个全序关系或者拟全序关系就升级为良序关系。
3. 函数
函数是单值的二元关系。
偏函数:定义在AXB上的函数F,即F属于AXB,且F是单值的,则F是A到B的偏函数。
全函数:F的定义域=A;共有|B|^|A|个,对于任意一个x属于A,都有|B|种选择;
函数的性质:单射,若x1!=x1,则f(x1)!=f(x2);或者f(x1)=f(x2)可推出x1=x2;
满射,对于任意的y属于B,都能找到x属于A,使得f(x)=y
满射个数的计算:n个不同的球放到m个不同的盒子里m!(n,m)
特征函数;
自然映射:R为A上的等价关系,对于任意的x属于A,f(x)=x在A/R中的等价类
c=fog,若c是双射的,则f是满射,g是单射
4.1自然数的定义
封闭:A在F下是封闭的,等价于F(A)属于A,F的映射不超出A
Peano系统五条公设:
对于一个三元组<M,F,e>,M是集合,F是M到M的封闭函数,e是首元素,如果这个三元组是皮亚诺系统,则需要满足:
e属于M
M在F下封闭
e不属于F(A)
F是单射
极小性公理:如果有一个集合A,A包含于M,且e属于A,且A在F下封闭,那么A=M
后继:A是集合,A的后继是AU{A}
归纳集:空集属于A,对任意属于A的元素(集合),A的后继也属于A。
自然数:自然数是属于每个归纳集的集合,即空集及其一切后继
自然数集:每个归纳集的交集,仍然是归纳集

任何自然数的元素均为它的子集。
任何自然数都不是自己的元素。

4.2自然数的性质
传递集:集合的元素的元素还是集合的元素
证明传递集的办法:

A是传递集等价于P(A)是传递集
每个自然数都是传递集
自然数集N是传递集

5.1 集合的等式、有穷集和无穷集
等势:两个集合等势等价于A B间存在双射
康托定理:N与R不等势,A与P(A)不等势
有穷集:与某个自然数n等势的集合或是不能与自身真子集建立双射的集合
5.2 基数的比较和运算
有穷基数和无穷基数;
基数的类;
优势&劣势:B比A优势,存在A到B的单射
基数的比较:直接构造单射
SB定理:如果A与B互相存在单射,则A与B等势,并且基数相等
可数集(可列集):基数小于啊列夫0;
A是无穷集,P(A)不是可数集
