word:
- Multiplying 镶嵌
- Parametric 参数
- Derivative 导数
- Integral || integrate 积分
- Recursion formula 递归公式
- Trigonometric substitution 山脚还原法
- Practical fraction decomposition 部分分解法
- Constant 常数
- Arbitrary 随机的
- Particular 特别的,详细的
- Power series ni级数
细节:
- 仔细思考求导公式,积分公式,到底是什么。
- 更好下x = 1/(2更好下x),1/x=-1/(x^2)
- 能不用分式就不同分式,比如三角函数,和分母都是X数时(不过这个时候要特别小心)
做完后的检查:
- 运算的内容。1 求导/积分 表+法则
- 剥洋葱,波完整了吗 ()5
- 积分大题 +c
- 化简的形似 分式和ln的整理
- 换元后一定要在变回去。
题型:
一大题(求导)
- 复合函数: 剥洋葱:求 拉拉的神马的导数后,就接着X求神马的导数。
- 对一个+式求导时,分开求每一项的导数,常数一定要变成0;栗子(xlnx-x+1)
- 相乘的那一项,就分成几个式子相加,不要拉下了,一个一个来,算完一个写一个,不要心算以免搞错。
- 注意负号问题。
二大题(隐函数法)
- 能2边直接求导,就直接求
- 不能就2边ln
- 利用tan ^2和sec^2的关系 找到山脚函数和x的关系,全部替换成那个东西
- 然后Y=反函数,和反函数的性质与反函数的求导。
三大题:(注意第二次求导,上下都要求不要只对一个求,其次注意求导过程。)
4-7大题:积分
- 积分公式
- 第一类积分
- 第二类积分(去掉根号,利用 a- 用sin ||-a用sec|| +a 用tan)
- 有理积分法 (式子可以分开,分别处理)
-
积分在寄回去后,是一个分数的次数,是除以这个分数的次数,反过来就是x,不要弄混了。
series 题 格式很重要。
8 大题:那个大题:
- l Matching at x= ,c
- l 找接口
- l 注意负号
9 大题(一般级数(series)判断放缩收敛)
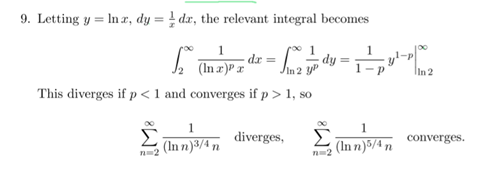
l 老是利用哪些方法。
10 大题 (ni级数判断收敛)
l 绝对值的比值法 和自己比
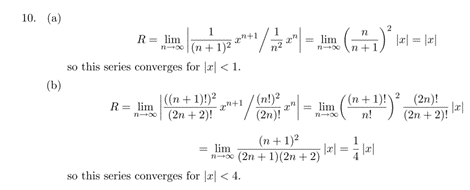
过程
泰勒展开:
- 利用泰勒表推导的时候,积分的时候是 对 dx 至于负号 比如ln1-x
- 泰勒的展开 前后的形式看清楚了,1 符号 2 次数,很重要,给的题目也是如此
11 大题:(泰勒展开,直接求)过程:


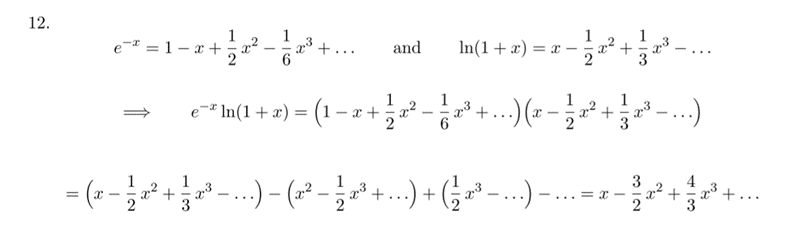

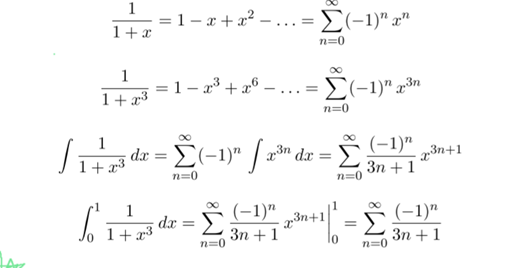
级数收敛的判断方法是什么?熟记7大判别方法,快速进行级数判敛| AP微积分专题级数部分 | TestDaily厚朴优学