深度优先用法之检测有无环

学习心得：课前没有好好预习，上课被老师问倒一片闷，o(︶︿︶)o，课后好好反思，以后要好好预习算法！！

首先是检测无向图里面是否有无环

（前提是无向环里没有自环边，平行边）

代码如下

//检测一个无向图是否有环
public class Cycle
{
    private boolean[] marked;
    private boolean hasCycle;
    
    public Cycle(Graph G)
    {
        marked = new boolean[G.V()];
        for(int s=0;s<G.V();s++)
            if(!marked[s])
                dfs(G,s,s);    //问题是这里为什么要两个顶点s,s了？？？？
    }
    
    private void dfs(Graph G,int v,int u)
    {
        marked[v] = true;
        for(int w:G.adj(v))
            if(!marked[w])
                dfs(G,w,v);  //如果一个没有被标记，就对它进行dfs,并且记录它的父节点
            else if(w!=u)    //如果一个节点已经被访问标记了，而且还不等于它的父节点（上一个节点），那就是环了！！
                hasCycle = true;
    }
    public boolean hasCycle()
    {return hasCycle;}
}

/*具体解释：
要判断无向图是否存在一个环，则必须是要求是有3个或3个以上的点顶点是两两相连的，使用深度优先搜索，每条边都会被访问两次，这样两个顶点之间就有两边，
但这不能说是环！！所以在dfs中就加多了一个变量u,用来记录当前节点的上一个节点，即为该节点的父节点。
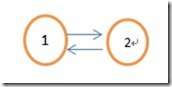
①对于两个节点的情况：

先进行dfs(1,1)，标记1号节点，
然后再dfs(2,1) （此时v=2,u=1），递归标记2号节点，之后又从回去检测1号节点（此时w=1），就出现w==u的情况，表明不满足环的条件

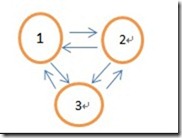
对于三个节点的情况：

假设先进行dfs(1,1)，标记1号节点，
然后再dfs(2,1) ,递归标记2号节点，
标记好2号节点后，继续dfs(3,2),递归标记3号节点，
标记好3号节点后，最后又会回到标记1号节点，此时v=3,u=2,w=1,满足条件，成环！！！

以此类推，大于3个顶点的也成立。
这是一个很巧妙的设计，可以用其他的办法来规避这种两个顶点的情况，但毫无疑问，这个在dfs中加多一个变量的方法，真是太赞了！！
*/