题意描述
需要你维护一个集合 (S), 并与给定的一些集合进行并集、交集、差集、异或等运算(其实题面已经很清楚了,不过多描述)。
解题思路
由于集合的值域较小,可以把它看成一段 01数列 的操作,其中数列中某个位置的值为 (1) 就代表集合 (S) 中有这个数。
先假设这个数列为 (a),那么如果 (a_1 = 1),(a_2 = 0),(a_3 = 1),(a_4 = 1),(a_5 = 0),那么集合 (S = {1,3,4})。
这里我将一一分析题目中的五种操作。
1. (S leftarrow S cup T)
其实就是把 (T) 集合所示的区间全部覆盖成 (1),对于 (S) 与 (T) 重合的地方,因为原来已经是 (1),被覆盖成 (1) 后仍不会改变。
操作:将集合 (T) 所示区间覆盖为 (1)
2. (S leftarrow S cap T)
交集本身的意思就是两个集合重合的部分,也就是说,集合 (S) 与集合 (T) 都有的地方才为 (1)。
同样,从反面考虑,如果某个数不在 (S) 里,或者不在 (T) 里,那么这个数一定不在 (S cap T) 里。
所以我们只需要排除 (S) 以外的数,再排除 (T) 以外的数,那么剩下的数所组成的集合一定就是 (S cap T)。
又因为我们所维护的集合 (S) 以外的数已经是 (0) 了,所以只需要在原来的基础上把 (T) 以外的数覆盖成 (0) 即可。
操作:将集合 (T) 以外的数所示区间覆盖为 (0)
3. (S leftarrow S - T)
(S - T) 的意思就是把集合 (S) 中,与 (T) 相交的部分去掉,这里放一张图。
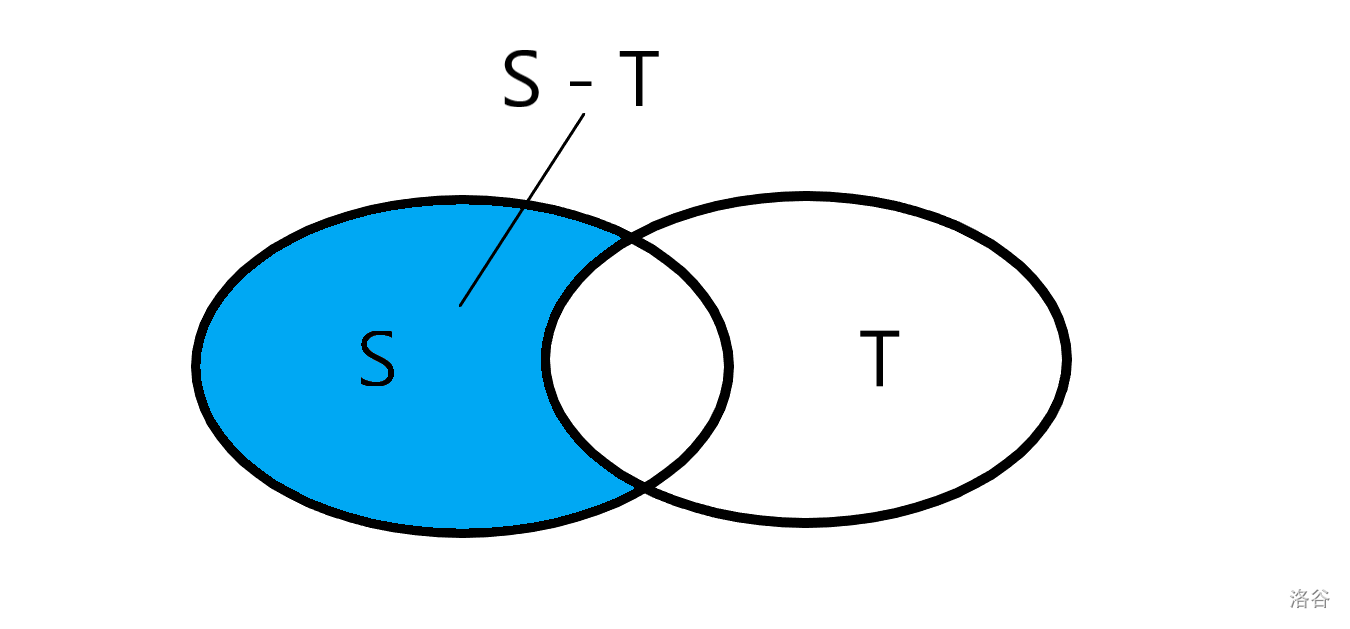
很明显,就是把 (T) 全部覆盖成 (0)。在 (T) 集合中,与 (S) 相交的被覆盖成了 (0),而对于 (S) 以外的地方,原本就是 (0),没有改变。
操作:将集合 (T) 所示区间覆盖为 (0)
4. (S leftarrow T - S)
同上,将 (T) 减去与 (S) 相交的部分并替代成原来的 (S) ,这里放一张图。

怎么办呢?这里有两种方法:
1.与上个操作一样,先记录下 (S) 所表示的区间,然后把 (T) 全部赋值成 (1),最后把记录的 (S) 所示区间全部赋值为 (0),原理同操作 (3) 一样。至于为什么要记录原来的 (S) 呢?因为把 (T) 所示区间赋值为 (1) 后,(S) 就变了,不是原来的 (S) 了。
2.我不想操作途中查询 (S) 怎么办?很简单,这里引入一个新操作——反转。
一开始,先把整个集合(就是值域)反转,这个时候原来的 (S) 集合全部变成了 (0),就成功地把 (S) 与 (T) 相交的部分去掉了。但是 (S) 以外的数都变成了 (1) 啊?
很简单。既然我们只想保留剩下的 (T) 的部分,那么就将 (T) 以外的数全部赋值为 (0)。因为与 (S) 相交的部分已经在之前去过了,所以剩下的就是 (T - S)。
这里推荐用第二种方法 (毕竟懒得记录)。
操作:将值域反转,再将集合 (T) 以外的数所示区间覆盖为 (0)
5. (S leftarrow S oplus T)
还是先放一张图。
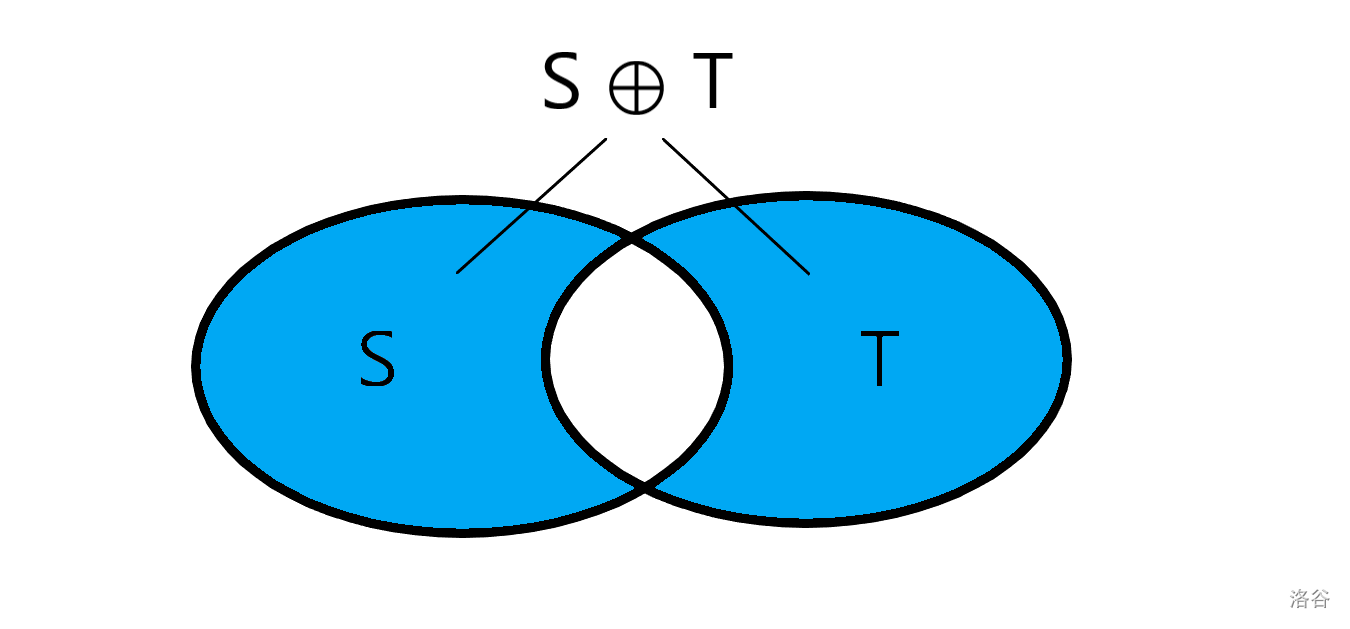
因为是异或,所以 (T) 与 (S) 相交的部分要变为 (0),而 (T) 的其他部分(没有与 (S) 相交的部分)则要变为 (1),这其实就是将 (T) 所在的区间整个反转(对着图看一下)。
操作:将集合 (T) 所示区间反转
代码实现
分析完所有操作后,你会惊奇地发现只剩下区间的覆盖和反转了,所以这是一道线段树的模板题。
我们需要记录一段区间有多少个 (1),以及覆盖和反转的两个 tag,在修改及询问的时候标记下传。
对于询问,只需要在最后询问一次,记录下每个位置的值,然后再输出。
时间复杂度约为 (O(Mlog N))((N) 为值域)。
注意:
由于存在开区间和闭区间且不可忽略,我们将其分别存储,值域*2即可。
数字可能为 (0),所以注意位置的分配,我这里习惯从 (1) 开始,所以对于每个数字 (k),其对应的位置是 (2k+1),两个数中间空的地方即为开区间。而且注意左开和右开不一样。
覆盖的 tag 记得一开始要记为 (-1)。
在进行覆盖操作及标记下传和的时候,要把反转标记赋为 (0),标记下传的时候先下传覆盖再下传反转。
反转及标记下传的时候是异或自己,而不是等于别人。
要讲的就那么多了。代码?拿来吧你!
代码(本人代码可能有点丑)
#include<bits/stdc++.h>
#define LC x<<1
#define RC x<<1|1
using namespace std;
int tree[800080],fz[800080],fg[800080],ans[200020];//fz:反转标记,fg:覆盖标记,ans:最终答案
char opt,c1,c2;
string s;
void pushup(int x){
tree[x]=tree[LC]+tree[RC];
}
void pushdown(int x,int l,int r){//标记下传
int mid=(l+r)>>1;
if(fg[x]!=-1){//先覆盖
tree[LC]=fg[x]*(mid-l+1);
tree[RC]=fg[x]*(r-mid);
fg[LC]=fg[x];
fg[RC]=fg[x];
//记得把反转标记变为 0
fz[LC]=0;
fz[RC]=0;
fg[x]=-1;
}
if(fz[x]){//再反转
tree[LC]=mid-l+1-tree[LC];
tree[RC]=r-mid-tree[RC];
//注意:是异或自己
fz[LC]=!fz[LC];
fz[RC]=!fz[RC];
fz[x]=0;
}
}
void mdffg(int x,int l,int r,int ql,int qr,int k){//覆盖操作
if(ql>qr) return;
if(ql<=l&&r<=qr){
tree[x]=k*(r-l+1);
fg[x]=k;
fz[x]=0;//记得反转标记赋为 0
return;
}
int mid=(l+r)>>1;
pushdown(x,l,r);
if(ql<=mid) mdffg(LC,l,mid,ql,qr,k);
if(mid<qr) mdffg(RC,mid+1,r,ql,qr,k);
pushup(x);
}
void mdffz(int x,int l,int r,int ql,int qr){//反转操作
if(ql>qr) return;
if(ql<=l&&r<=qr){
tree[x]=r-l+1-tree[x];
fz[x]=!fz[x];
return;
}
int mid=(l+r)>>1;
pushdown(x,l,r);
if(ql<=mid) mdffz(LC,l,mid,ql,qr);
if(mid<qr) mdffz(RC,mid+1,r,ql,qr);
pushup(x);
}
void query(int x,int l,int r){
if(l==r){
ans[l]=tree[x];//记录答案
return;
}
int mid=(l+r)>>1;
pushdown(x,l,r);
query(LC,l,mid);
query(RC,mid+1,r);
}
void solve(){
query(1,1,200000);
if(!tree[1]){//如果所有数字的值都为 0,那么 S 就是空集
printf("empty set
");
return;
}
bool ck=0;
//记得处理并集
for(int i=1;i<=200000;i++){
if(!ck&&ans[i]){
ck=1;
if(i%2==0) printf("(");
else printf("[");
printf("%d,",(i-1)>>1);
}
if(ck&&!ans[i+1]){
ck=0;
printf("%d",i>>1);
if(i%2==0) printf(") ");
else printf("] ");
}
}
printf("
");
}
int main(){
for(int i=0;i<=800079;i++) fg[i]=-1;//记得赋为-1
while(cin>>opt){
int l,r;
cin>>c1;
scanf("%d,%d",&l,&r);
cin>>c2;
//处理括号,注意左开和右开不一样
if(c1=='(') l=2*l+2;
else l=2*l+1;
if(c2==')') r=2*r;
else r=2*r+1;
//5个操作,具体已在上面讲解
//这里所有的200000即为值域
if(opt=='U') mdffg(1,1,200000,l,r,1);
if(opt=='I'){
mdffg(1,1,200000,1,l-1,0);
mdffg(1,1,200000,r+1,200000,0);
}
if(opt=='D') mdffg(1,1,200000,l,r,0);
if(opt=='C'){
mdffz(1,1,200000,1,200000);
mdffg(1,1,200000,1,l-1,0);
mdffg(1,1,200000,r+1,200000,0);
}
if(opt=='S') mdffz(1,1,200000,l,r);
}
solve();//输出最终答案
}