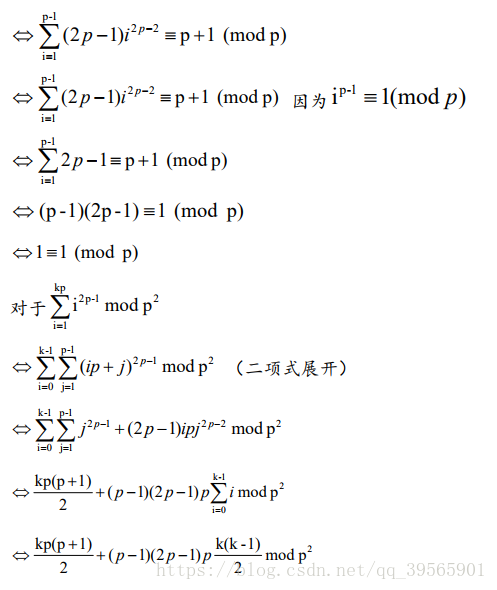JZOJ 100027. 【NOIP2017提高A组模拟7.7】表达式
题目
Description
Input
一行两个整数k,p。
Output
一行一个整数表示答案。
Sample Input
1 3
Sample Output
6
Data Constraint
对于20%的数:
k
∗
p
<
=
1
0
5
k*p<=10^5
k∗p<=105。
对于另外20%的数据k=1。
对于70%的数据:
k
∗
p
<
=
1
0
9
k*p<=10^9
k∗p<=109。
对于100%的数据:k,p<=
1
0
9
10^9
109。
题解
方法一
(内容来源:https://jzoj.net)
方法二
当
p
=
2
p=2
p=2,答案为
1
,
0
,
1
,
0
,
1
,
0
,
1
,
0
,
1
,
0
…
…
1,0,1,0,1,0,1,0,1,0……
1,0,1,0,1,0,1,0,1,0……。
当
p
=
3
p=3
p=3,答案为
6
,
6
,
0
,
6
,
6
,
0
,
6
,
6
,
0
…
…
6,6,0,6,6,0,6,6,0……
6,6,0,6,6,0,6,6,0……。
当
p
=
5
p=5
p=5,答案为
15
,
10
,
10
,
15
,
0
,
15
,
10
,
10
,
15
,
0
…
…
15,10,10,15,0,15,10,10,15,0……
15,10,10,15,0,15,10,10,15,0……。
当
p
=
7
p=7
p=7,答案为
28
,
14
,
7
,
7
,
14
,
28
,
0
,
28
,
14
,
7
,
7
,
14
,
28
,
0
…
…
28,14,7,7,14,28,0,28,14,7,7,14,28,0……
28,14,7,7,14,28,0,28,14,7,7,14,28,0……。
当
p
=
11
p=11
p=11,答案为
66
,
22
,
110
,
88
,
77
,
77
,
88
,
110
,
22
,
66
,
0
…
…
66,22,110,88,77,77,88,110,22,66,0……
66,22,110,88,77,77,88,110,22,66,0……。
…
…
……
……
这样好像看不出什么,但可以发现两点:
1、答案有循环,且每个循环节是回文的,
k
∣
p
k|p
k∣p时答案为0.
2、
p
>
2
p>2
p>2时非
0
0
0的答案为
p
p
p的倍数。
那么我们把每个循环节前一半的答案除以
p
p
p找出来。
当
p
=
3
p=3
p=3:
2
2
2。
当
p
=
5
p=5
p=5:
3
,
2
3,2
3,2。
当
p
=
7
p=7
p=7:
4
,
2
,
1
4,2,1
4,2,1。
当
p
=
11
p=11
p=11:
6
,
2
,
10
,
8
,
7
6,2,10,8,7
6,2,10,8,7。
当
p
=
13
p=13
p=13:
7
,
2
,
11
,
8
,
6
,
5
7,2,11,8,6,5
7,2,11,8,6,5。
当
p
=
17
p=17
p=17:
9
,
2
,
13
,
8
,
4
,
1
,
16
,
15
9,2,13,8,4,1,16,15
9,2,13,8,4,1,16,15。
当
p
=
23
p=23
p=23:
12
,
2
,
16
,
8
,
1
,
18
,
13
,
9
,
6
,
4
,
3
12,2,16,8,1,18,13,9,6,4,3
12,2,16,8,1,18,13,9,6,4,3。
…
…
……
……
通过观察发现,每一行的第一项为
p
+
1
2
\frac{p+1}{2}
2p+1。
后面的呢?
不难发现(其实很难),每一项为一个公差为
1
1
1的等差数列的前缀和,再对
p
p
p取模。
举例:
当
p
=
23
p=23
p=23,等差数列
12
,
13
,
14
,
15
,
16
,
17
,
18
,
19
,
20
,
21
,
22
12,13,14,15,16,17,18,19,20,21,22
12,13,14,15,16,17,18,19,20,21,22。
当
p
=
23
p=23
p=23,前缀和
12
,
25
,
39
,
54
,
70
,
87
,
105
,
124
,
144
,
165
,
187
12,25,39,54,70,87,105,124,144,165,187
12,25,39,54,70,87,105,124,144,165,187。
当
p
=
23
p=23
p=23,对
p
p
p取模后
12
,
2
,
16
,
8
,
1
,
18
,
13
,
9
,
6
,
4
,
3
12,2,16,8,1,18,13,9,6,4,3
12,2,16,8,1,18,13,9,6,4,3。
这样就可以快速实现了,注意
p
=
2
p=2
p=2要特判。
代码
方法二的代码。
#include<cstdio>
#include<cstring>
using namespace std;
int main()
{
int k,p;
scanf("%d%d",&k,&p);
if(p==2)
{
printf("%d",k%2);
return 0;
}
k%=p;
if(k==0)
{
printf("0");
return 0;
}
if(k>p/2) k=p-k;
long long s=(p+1)/2;
long long t=s+k-1;
printf("%lld",(s+t)*k/2%p*p);
return 0;
}