JZOJ 6309. 完全背包（矩阵max）

JZOJ 6309. 完全背包

题目

Description

Input

Output

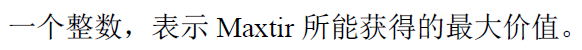
Sample Input

Sample 1:
2 15
3 2
5 3

Sample 2:
3 70
71 100
69 1
1 2

Sample Output

Sample 1:
10

Sample 2:
140

Data Constraint

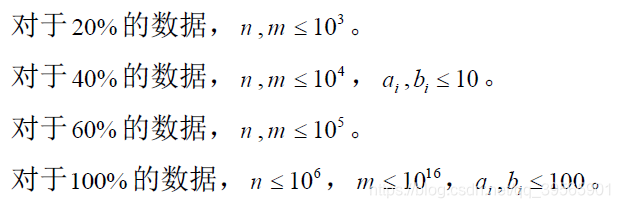
题解

• 乍一看，这不就是非常裸的完全背包吗？？？
• 再看看范围，背包容量极大，但是，物品的代价却很小。
• 如果直接打最裸的完全背包，时间复杂度是$O(nm)$，能得到$20$分；
• 如果对于代价相同的，只用收益最大的一个转移，时间复杂度是$O(Ma{x}_{a_i}m）$，能得到$60$分；
• 看到这么大的$m$，不难想到矩阵。
• 设初始一维矩阵$v[i](i\in [0,100])$表示花费$i$的代价最大能有多少收益（可以选多个，如同容量为$i$的完全背包），
• 不难发现，有了这个就可以用两个$i\in [0-100]$得到$i\in [100,200]$，用两个$i\in [100,200]$得到$i\in [300,400]$……以此类推。
• 那么自然想到矩阵快速幂，因为每次可以得出$100$个的答案，所以快速幂的指数设为$\lfloor \frac{m}{100}\rfloor +1$，
• 每次先用当前的矩阵$f$与自己相加取$max$，然后用$v$更新一遍$f$，
• 如果指数为奇数，再用$f$与$v$相加得到新的$f$，
• 最后的答案即为$f[m\mathrm{m}\mathrm{o}\mathrm{d}100]$。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
ll v[110],f[110],c[110];
void ksm(ll x)
{
	int i,j;
	if(x==1) 
	{
		for(i=0;i<=100;i++) f[i]=v[i];
		return;
	}
	ksm(x/2);
	memset(c,0,sizeof(c));
	for(i=0;i<=100;i++)
		for(j=0;j<=100;j++)
			if(i+100-j>=0&&i+100-j<=100) c[i]=max(c[i],f[j]+f[i+100-j]);
	for(i=0;i<=100;i++)
		for(j=0;j<=i;j++) c[i]=max(c[i],c[j]+v[i-j]);
	for(i=0;i<=100;i++) f[i]=c[i];
	if(x%2)
	{
		memset(c,0,sizeof(c));
		for(i=0;i<=100;i++)
			for(j=0;j<=100;j++)
				if(i+100-j>=0&&i+100-j<=100) c[i]=max(c[i],f[j]+v[i+100-j]);
		for(i=0;i<=100;i++)
			for(j=0;j<=i;j++) c[i]=max(c[i],c[j]+v[i-j]);
		for(i=0;i<=100;i++) f[i]=c[i];
	}
}
int main()
{
	int n,i,j,x,y;ll m;
	scanf("%d%lld",&n,&m);
	for(i=1;i<=n;i++)
	{
		scanf("%d%d",&x,&y);
		if(y>v[x]) v[x]=y;
	}
	for(i=1;i<=100;i++) 
		for(j=1;j<i;j++) v[i]=max(v[i],v[j]+v[i-j]);
	ksm(m/100+1);
	printf("%lld",f[m%100]);
	return 0;
}