JZOJ 6316. djq的朋友圈
题目
Description

Input

Output
一个整数表示最多的盟友数。
Sample Input
Sample 1:
7 8
1 2 0
1 3 0
2 4 0
4 5 0
3 4 1
2 5 1
5 7 1
1 7 1
Sample 2:
8 24
5 8 1
6 3 1
2 8 0
4 6 1
4 1 1
2 3 1
5 4 1
5 1 0
2 6 0
1 3 0
8 7 1
8 4 1
1 7 1
7 2 1
8 1 1
3 4 0
3 7 0
7 6 0
5 2 0
6 1 1
5 3 0
5 7 1
6 5 0
6 8 0
Sample Output
Sample 1:
4
Sample 2:
3
Data Constraint

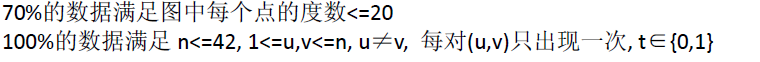
Hint
样例1 中,如果顺序为“7,2,3”,可以使得 2,3,4,5 都和 djq 成为盟友。
题解
- 这题的题意看起来有点复杂。。。
- 首先可以发现,与 1 1 1最短距离大于 2 2 2的点最后一定是不确定的,所以忽略它们,
- 设集合 A A A为所有与 1 1 1有边相连的点,也就是最初已经确定的,
- 集合 B B B为所有在 A A A集合外且不为 1 1 1的与 A A A集合任意点相邻的点,也就是能间接确定的,
- 其它的都没法确定。
- 现在只用考虑从 A A A集合中选点的顺序,
- 对于 70 % 70\% 70%的数据,直接状压当前 A A A集合中已经选过的点,
- 每次枚举一个状态,将已经选过的点所能连向的所有在 B B B中的点标记,标记的就是被确定关系的
- 再枚举一个还没选过的点,它所连向所有在的 B B B中的点,如果还未被标记的点即可以确定关系,统计出有多少个“盟友”,更新状态。
- 最后还要再加上 A A A集合中的“盟友”。
- 对于全部数据,做法也是类似的,
- 如果 A A A集合小于 B B B集合大小,同 70 % 70\% 70%的做法,
- 否则状压 B B B中的点,做法类似,
- 还是枚举 A A A中的点,但不用判断它是否选过,只需要看它能确定多少 B B B中的点,然后更新状态。
- 最后仍然要加上 A A A集合中的“盟友”。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int last[45],next[1800],to[1800],re[1800],len=0;
int nu[45],bz[45],f[2100000];
int p[45],s1[45],s2[45],r[45][45];
void add(int u,int v,int x)
{
to[++len]=v;
re[len]=x;
next[len]=last[u];
last[u]=len;
r[u][v]=x;
}
int main()
{
int n,m,i,j,k,u,v,x;
scanf("%d%d",&n,&m);
memset(r,255,sizeof(r));
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&x);
add(u,v,x),add(v,u,x);
}
s1[0]=s2[0]=0;
for(i=last[1];i;i=next[i]) bz[to[i]]=1,s1[++s1[0]]=to[i],nu[to[i]]=s1[0];
for(i=1;i<=n;i++) if(bz[i]==1)
for(j=last[i];j;j=next[j]) if(!bz[to[j]]&&to[j]>1) bz[to[j]]=2,s2[++s2[0]]=to[j],nu[to[j]]=s2[0];
if(s1[0]<21)
{
memset(f,0,sizeof(f));
for(i=0;i<(1<<s1[0]);i++) if(i==0||f[i])
{
memset(p,0,sizeof(p));
for(j=1;j<=s1[0];j++) if(i&(1<<(j-1)))
for(k=last[s1[j]];k;k=next[k]) if(bz[to[k]]==2) p[to[k]]=i+1;
for(j=1;j<=s1[0];j++) if((i&(1<<(j-1)))==0)
{
int s=0;
for(k=last[s1[j]];k;k=next[k]) if(bz[to[k]]==2&&p[to[k]]<=i) s+=r[1][s1[j]]==re[k];
f[i+(1<<(j-1))]=max(f[i+(1<<(j-1))],f[i]+s);
}
}
int s=0;
for(i=1;i<=s1[0];i++) s+=!r[1][s1[i]];
printf("%d
",f[(1<<s1[0])-1]+s);
}
else
{
memset(f,0,sizeof(f));
for(i=0;i<(1<<s2[0]);i++) if(i==0||f[i])
{
for(j=1;j<=s1[0];j++)
{
int s=0,t=0;
for(k=last[s1[j]];k;k=next[k])
if(bz[to[k]]==2&&!(i&(1<<(nu[to[k]]-1)))) s+=r[1][s1[j]]==re[k],t+=1<<(nu[to[k]]-1);
f[i+t]=max(f[i+t],f[i]+s);
}
}
int s=0;
for(i=1;i<=s1[0];i++) s+=!r[1][s1[i]];
printf("%d
",f[(1<<s2[0])-1]+s);
}
return 0;
}