prufer序列
引入
- 如何为有标号无根树判重?
- 这里可以用到prufer序列——
初识
- prufer序列是与无根树对应的序列。
- 每一棵无根树(点数 n ≥ 2 n≥2 n≥2)都可以得到与其唯一对应的序列,且序列长度为 n − 2 n-2 n−2,
- 通过特定的方式,可以将无根树转为prufer序列,
- 也可以通过prufer序列和确定的点集,还原一棵无根树。
操作
一、无根树转prufer序列
- 每次选取当前度数为 1 1 1且编号最小的点(以保证序列唯一性),将与其相连的点(只有一个)的编号加入prufer序列中,并将该点(指选取的这个点,不是与它相连的这个点)删除。
- 直到树上只剩两个点时停止操作,此时得到长度为 n − 2 n-2 n−2的prufer序列。
- 例如一个无根树,边集为 { ( 1 , 2 ) , ( 2.3 ) , ( 1 , 4 ) , ( 4 , 5 ) , ( 4 , 6 ) } { (1,2),(2.3),(1,4),(4,5),(4,6)} {(1,2),(2.3),(1,4),(4,5),(4,6)},
- 选择 3 3 3号点,此时序列为 { 2 } {2} {2}
- 选择 2 2 2号点,此时序列为 { 2 , 1 } {2,1} {2,1}
- 选择 1 1 1号点,此时序列为 { 2 , 1 , 4 } {2,1,4} {2,1,4}
- 选择 5 5 5号点,此时序列为 { 2 , 1 , 4 , 4 } {2,1,4,4} {2,1,4,4}
- 此时操作结束。
二、prufer序列转无根树
- 每次选择不在prufer序列且在点集中的编号最小的点,将其与prufer序列的第一项连边,并将prufer序列的第一项删除,点集中选择的这个点删除。
- 最后prufer序列为空时,再将点集中剩下的两个点连边。
- 例如上文的prufer序列 { 2 , 1 , 4 , 4 } {2,1,4,4} {2,1,4,4},点集为 { 1 , 2 , 3 , 4 , 5 , 6 } {1,2,3,4,5,6} {1,2,3,4,5,6},
- 选出 2 2 2和 3 3 3号点连边,此时序列为 { 1 , 4 , 4 } {1,4,4} {1,4,4},点集为 { 1 , 2 , 4 , 5 , 6 } {1,2,4,5,6} {1,2,4,5,6},
- 选出 1 1 1和 2 2 2号点连边,此时序列为 { 4 , 4 } {4,4} {4,4},点集为 { 1 , 4 , 5 , 6 } {1,4,5,6} {1,4,5,6},
- 选出 4 4 4和 1 1 1号点连边,此时序列为 { 4 } {4} {4},点集为 { 4 , 5 , 6 } {4,5,6} {4,5,6},
- 选出 4 4 4和 5 5 5号点连边,此时序列为 { } {} {},点集为 { 4 , 6 } {4,6} {4,6},
- 最后再将 4 4 4和 6 6 6号点连边,
- 此时完全还原一棵树。
性质
一、关于唯一性
- 在初始部分提到过的,无根树和prufer序列一一对应。
二、关于点的度数
- 通过构造过程可知,每个点在度数为 1 1 1时被删去,其余时刻被加入prufer序列一次则它的度数减少一。
- 所以每个点在prufer序列中的出现次数为它的度数 d − 1 d-1 d−1。
三、无根树的计数(一)
- 点集大小为 n n n时,prufer序列长度为 n − 2 n-2 n−2,意味着序列中每个数的可能有 n n n种,则整个序列的构造方案有 n n − 2 n^{n-2} nn−2种,
- 再根据prufer序列和无根树一一对应,则点集为 n n n的带标号无根树的构造方案有 n n − 2 n^{n-2} nn−2种,即 n n n个点构成的完全图中,生成树的个数为 n n − 2 n^{n-2} nn−2。
四、无根树的计数(二)
- 点集大小为 n n n,且每个点的度数 d 1 n d_{1~n} d1 n确定时,则每个数在prufer序列中出现次数确定,
- 那么prufer序列的构造方案为 ( n − 2 ) ! (n-2)! (n−2)!再去掉同一个数重复的情况,就是 ( n − 2 ) ! Π ( d i − 1 ) ! frac{(n-2)!}{Pi (d_i-1)!} Π(di−1)!(n−2)!。
应用
- 一般来说,prufer序列用于方便树的计数,对于树的形态重复的判定可以转化为prufer序列重复的判定,大大方便计算。
- 利用性质二,关于对点的度数有限制的树的计数,也可以联想到转化为prufer序列构造的方案数。
例题

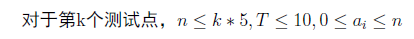
- 直接转化为prufer序列的计数,设 f i , j , k f_{i,j,k} fi,j,k表示选到第 i i i个点,用了 j j j个点,在prufer序列中加入了 k k k个数的方案数,转移时枚举当前点选或不选,选的话选加入几个进prufer序列中(加入 0 0 0个也算选,注意上限为 a i − 1 a_i-1 ai−1),然后用组合数计算更新后的方案数:
- f i , j , k = f i − 1 , j , k + Σ l = 0 a i − 1 f i − 1 , j − 1 , k − l × ( k l ) f_{i,j,k} = f_{i-1,j,k}+Sigma_{l=0}^{a_i-1} f_{i-1,j-1,k-l} × {k choose l} fi,j,k=fi−1,j,k+Σl=0ai−1fi−1,j−1,k−l×(lk)
- 时间复杂度 O ( T n 4 ) O(Tn^4) O(Tn4)。