滤波器的技术指标
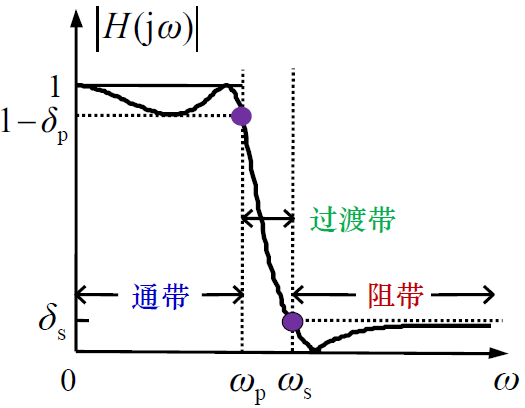
$w_p$:通带截止频率
$w_s$:阻带截止频率
$delta_p$:通带波动
$delta_s$:阻带波动
衰减单位是db
滤波器系数、脉冲响应、频率响应的关系:滤波器变换,时域卷积等于频域乘积,滤波操作在时域表现为输入信号与滤波器脉冲响应的卷积;从频域上看滤波器操作表现为,输入信号的傅立叶变换和脉冲响应的傅立叶变换做乘积。
低通滤波器:只允许某一频率以下的信号无衰减地通过滤波器,其分界处的频率称为截止频率。<p id="lowpass" style="#lowpass:hover{}">图片</p>
高通滤波器:规定高于设定临界值频率(fc)的信号能正常通过,而低于设定临界值频率(fc)的信号则被阻隔和衰减。
带通滤波器:允许特定频率信号通过的滤波器,阻隔和衰减该频带上下频率的信号。带通滤波器可以看做是由高通和低通滤波器协同作用的结果,高通和低通滤波器的截止频率可作为通带的下限频率和上限频率(图3中的L和U点)。其主要参数是中心频率和带宽,上限频率和下限频率之差就是滤波器的带宽。
带阻滤波器:能通过大多数频率分量,但将某些范围的频率分量衰减到极低水平的滤波器,与带通滤波器的概念相对。其中陷波滤波器(notch filter)是一种特殊的带阻滤波器,它的阻带范围极小。
陷波滤波器:可以在某一个频率点迅速衰减输入信号,以达到阻碍此频率信号通过的滤波效果,主要用在电路上滤除不需要的频率的信号。
对于FIR滤波器,滤波器系数即为脉冲响应,因此,对于FIR滤波器,系数的FFT变换即为滤波器的频率响应曲线
巴特沃斯滤波器
butterworth低通滤波器的频域特性
$$|H(jw)|^2=frac{1}{1+(frac{omega }{omega _c})^{2N}}$$
N:滤波器的阶数
$omega _c$:3dB截频

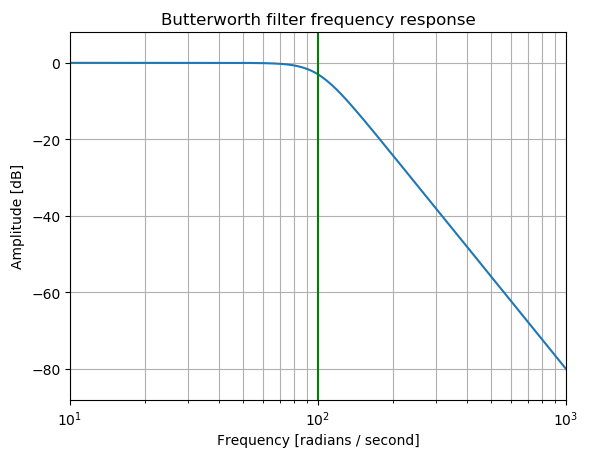
典型BW低通滤波器的幅度响应
特点:在通带的频率响应曲线最平滑
Python实现
scipy.signal.butter(N, Wn, btype='low', analog=False, output='ba')
输入
- N:滤波器的阶数
- Wn:截止频率,对于巴特沃斯滤波器,这是增益下降到通带$frac{1}{sqrt 2}$的点(即“-3db点”)。
- 对于数字滤波器:Wn与fs的单位相同Hz(fs是采样率),在MATLAB中Wn是归一化截止频率(0,1),Wn=截止频率/信号频率,(信号频率=采样率的一半,奈奎斯特采样定理)。归一化频率=1,截止频率$w_c$代表采样频率,0.5代表奈奎斯特频率
- 对于模拟滤波器:Wn是角频率(弧度/秒,radians/second)
- btype:滤波器的类型{'lowpass','highpass','bandpass','bandstop'}
- analog:如果为True,则返回模拟滤波器,否则返回数字滤波器。
输出
- b,a:滤波器系数, a为分母,b为分子。
scipy.signal.freqs(b, a, worN=200, plot=None)
计算模拟滤波器的频率响应H(w)。
$$H(w)=frac{b[0]*(jw)**M+b[1]*(jw)**(M-1)+...+b[M]}{ a[0]*(jw)**N + a[1]*(jw)**(N-1) + ... + a[N]}$$
参数
- b,a:线性滤波器的分子和分母,
- worN:可选,如果为None,则计算响应曲线的有趣部分周围的200个频率。如果是一个整数,则计算那么多频率。
返回
- w:计算h的角频率
- h:频率响应(在该频率值得振幅)
scipy.signal.freqz(b, a=1, worN=512, whole=False, plot=None)
计算数字滤波器的频率响应。
$$H(e^{jw})=frac{B(e^{jw})}{A(e^{jw})}=frac{b(1)+b(2)e^{-jw}+...+b(n+1)e^{-jwn}}{a(1)+a(2)e^{-jw}+...+a(m+1)e^{-jwm}}$$
参数
- b,a:线性滤波器的分子和分母
- worN:如果为None(默认值),则计算在单位圆周围等间隔的512个频率。如果是一个整数,则计算那么多频率。如果是array_like,则计算给定频率的响应(以弧度/样本为单位)。
返回
- w:计算h的频率,单位与fs相同。默认情况下,w被归一化为$[0,1)*pi$范围(radians/sample),例如对于一个采样频率为1000Hz的系统,300Hz则对应300/500=0.6。若要将归一化频率转换为单位圆上的弧度,则将归一化值乘以π即可。图中的0.5表示的是0.5π(rad),即为w = 0.5π, 由 w = 2 * pi * f / fs 得到 f = w * fs / 2pi,即 f = 0.5 * fs / 2 ,因为 fs = 122.88MHz,所以截止频率 f = 30.72MHz。
- h:频率响应,以复数表示
scipy.signal.lfilter(b, a, x, axis=-1, zi=None)
使用IIR或FIR滤波器沿一维过滤数据。使用数字滤波器过滤数据序列x。
输入
- b,a:分子和分母,即滤波器系数
- x:输入数据
返回:数字滤波器的输出
from scipy.signal import butter, lfilter from scipy import signal import numpy as np import matplotlib.pyplot as plt b, a = signal.butter(4, 100, 'low', analog=True) # 设计N阶数字或模拟Butterworth滤波器并返回滤波器系数 w, h = signal.freqs(b, a) # 根据系数计算滤波器的频率响应,w是角频率,h是频率响应 plt.semilogx(w, 20 * np.log10(abs(h))) plt.title('Butterworth filter frequency response') plt.xlabel('Frequency [radians / second]') plt.ylabel('Amplitude [dB]') plt.margins(0, 0.1) plt.grid(which='both', axis='both') plt.axvline(100, color='green') # cutoff frequency plt.show()
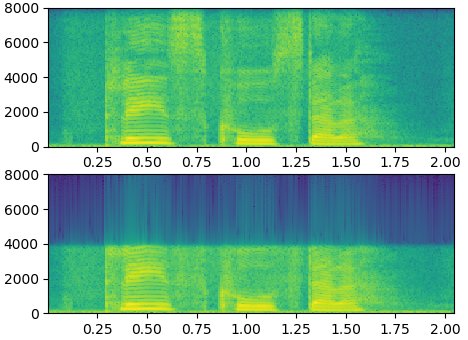
提取窄带语音信号
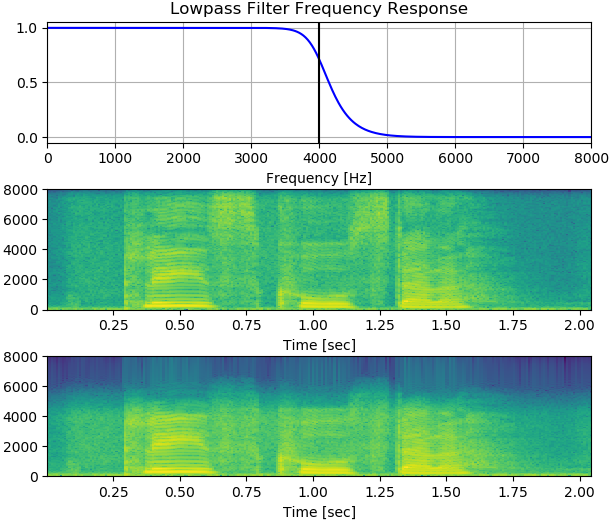
对采样率为16000Hz,奈奎斯特频率为8000Hz的语音,通过巴特沃斯低通滤波器,滤除高于4000Hz频率的语音,提取低频语音。过滤出的信号,在采样率相同的情况下,频率只有原来的一半。
import librosa import numpy as np from scipy.signal import butter, lfilter, freqz import matplotlib.pyplot as plt def butter_lowpass(cutoff, fs, order=5): # cutoff:截止频率 # fs 采样率 nyq = 0.5 * fs # 信号频率 normal_cutoff = cutoff / nyq # 正常截止频率=截止频率/信号频率 b, a = butter(order, normal_cutoff, btype='lowpass', analog=False) return b, a def butter_lowpass_filter(data, cutoff, fs, order=5): b, a = butter_lowpass(cutoff, fs, order=order) y = lfilter(b, a, data) return y # Filter requirements. order = 10 fs = 16000 # 采样率, Hz cutoff = 4000 # 滤波器的期望截止频率,Hz # 得到滤波器系数,这样我们就可以检查它的频率响应。 b, a = butter_lowpass(cutoff, fs, order) # 绘制频率响应 w, h = freqz(b, a) plt.subplot(3, 1, 1) plt.plot(0.5*fs*w/np.pi, np.abs(h), 'b') plt.axvline(cutoff, color='k') plt.xlim(0, 0.5*fs) plt.title("Lowpass Filter Frequency Response") plt.xlabel('Frequency [Hz]') data, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) # 48000--->16000 y = butter_lowpass_filter(data, cutoff, fs, order) plt.subplot(3, 1, 2) plt.specgram(data, Fs=16000, scale_by_freq=True, sides='default') plt.xlabel('Time [sec]') plt.subplot(3, 1, 3) plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default') plt.xlabel('Time [sec]') plt.show()
切比雪夫I形状滤波器
CB I型低通滤波器的频域特性
$$|H(jw)|^2=frac{1}{1+varepsilon ^2C_N^2(frac{w}{w_c})}$$
N:滤波器的阶数
$varepsilon$:通带波纹
$omega _c$:通带截频
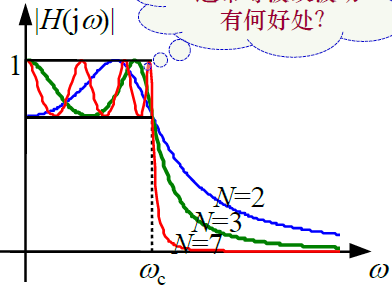
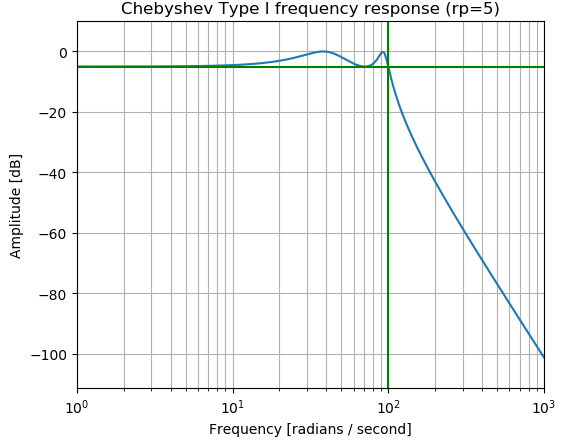
图 CB I型低通滤波器的幅度响应
特点:通带是等波动的,阻带是单调的
scipy.signal.cheby1(N, rp, Wn, btype='low', analog=False, output='ba')
Chebyshev I型数字和模拟滤波器,设计N阶数字或模拟Chebyshev I型滤波器并返回滤波器系数。
参数:
- N:滤波器的阶数
- rp:通带中允许的最大纹波低于单位增益,以分贝为单位,正数
- Wn:对于数字滤波器:Wn应该归一化为(0,1),Wn=截止频率/信号频率,(信号频率=采样率的一半,奈奎斯特采样定理)对于模拟滤波器:Wn是角频率,弧度/样本,rad/s
- btype:滤波器的类型{'lowpass','highpass','bandpass','bandstop'}
- analog:如果为True,则返回模拟滤波器,否则返回数字滤波器。
- output:默认“ba”,输出分子和分母
返回
- b,a:滤波器系数, a为分母,b为分子。
import numpy as np from scipy import signal import matplotlib.pyplot as plt b, a = signal.cheby1(4, 5, 100, 'low', analog=True) w, h = signal.freqs(b, a) plt.semilogx(w, 20 * np.log10(abs(h))) plt.title('Chebyshev Type I frequency response (rp=5)') plt.xlabel('Frequency [radians / second]') plt.ylabel('Amplitude [dB]') plt.margins(0, 0.1) plt.grid(which='both', axis='both') plt.axvline(100, color='green') # cutoff frequency plt.axhline(-5, color='green') # rp plt.show()
切比雪夫II形状滤波器
CB II型低通滤波器的频域特性
$$|H(jw)|^2=1-frac{1}{1+varepsilon ^2C_N^2(frac{w}{w_c})}$$
N:滤波器的阶数
$varepsilon$:阻带波纹
$omega _c$:阻带截频
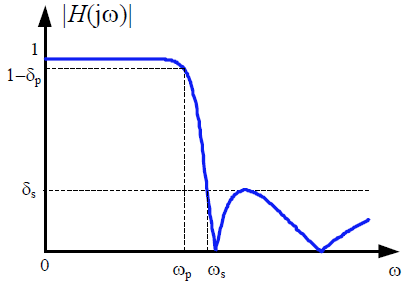
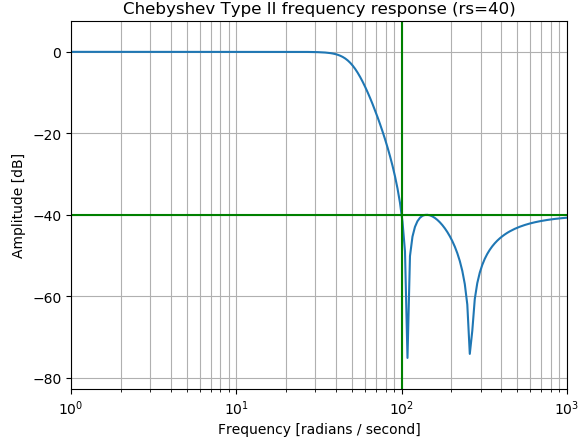
图 CB II型低通滤波器的幅度响应
特点:通带是单调的,阻带是等波动的
scipy.signal.cheby2(N, rs, Wn, btype='low', analog=False, output='ba')
Chebyshev II型数字和模拟滤波器,设计N阶数字或模拟Chebyshev II型滤波器并返回滤波器系数。
参数:
- N:滤波器的阶数
- rs:阻带所需最小衰减,以分贝为单位,正数
- Wn:对于数字滤波器:Wn应该归一化为(0,1),Wn=截止频率/信号频率,(信号频率=采样率的一半,奈奎斯特采样定理)对于模拟滤波器:Wn是角频率,弧度/样本,rad/s
- btype:滤波器的类型{'lowpass','highpass','bandpass','bandstop'}
- analog:如果为True,则返回模拟滤波器,否则返回数字滤波器。
- output:默认“ba”,输出分子和分母
返回
- b,a:滤波器系数, a为分母,b为分子。
from scipy import signal import numpy as np import matplotlib.pyplot as plt b, a = signal.cheby2(4, 40, 100, 'low', analog=True) w, h = signal.freqs(b, a) plt.semilogx(w, 20 * np.log10(abs(h))) plt.title('Chebyshev Type II frequency response (rs=40)') plt.xlabel('Frequency [radians / second]') plt.ylabel('Amplitude [dB]') plt.margins(0, 0.1) plt.grid(which='both', axis='both') plt.axvline(100, color='green') # cutoff frequency plt.axhline(-40, color='green') # rs plt.show()
椭圆低通滤波器
椭圆模拟低通滤波器的频域特性
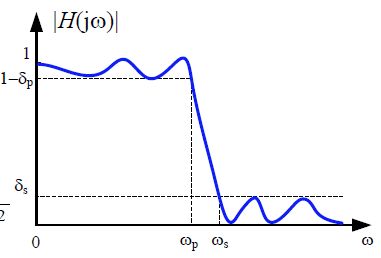
图 椭圆低通滤波器的幅度相应
特点:通带和阻带都等波动
scipy.signal.ellip(N, rp, rs, Wn, btype='low', analog=False, output='ba')
椭圆数字和模拟滤波器,设计N阶数字或模拟椭圆滤波器并返回滤波器系数。
参数:
- N:滤波器的阶数
- rp:通带中允许的最大纹波低于单位增益,以分贝为单位,正数
- rs:阻带所需最小衰减,以分贝为单位,正数
- Wn:对于数字滤波器:Wn应该归一化为(0,1),Wn=截止频率/信号频率,(信号频率=采样率的一半,奈奎斯特采样定理)对于模拟滤波器:Wn是角频率,弧度/样本,rad/s
- btype:滤波器的类型{'lowpass','highpass','bandpass','bandstop'}
- analog:如果为True,则返回模拟滤波器,否则返回数字滤波器。
- output:默认“ba”,输出分子和分母
返回
- b,a:滤波器系数, a为分母,b为分子。
import numpy as np from scipy import signal import matplotlib.pyplot as plt b, a = signal.ellip(4, 5, 40, 100, 'low', analog=True) w, h = signal.freqs(b, a) plt.semilogx(w, 20 * np.log10(abs(h))) plt.title('Elliptic filter frequency response (rp=5, rs=40)') plt.xlabel('Frequency [radians / second]') plt.ylabel('Amplitude [dB]') plt.margins(0, 0.1) plt.grid(which='both', axis='both') plt.axvline(100, color='green') # cutoff frequency plt.axhline(-40, color='green') # rs plt.axhline(-5, color='green') # rp plt.show()
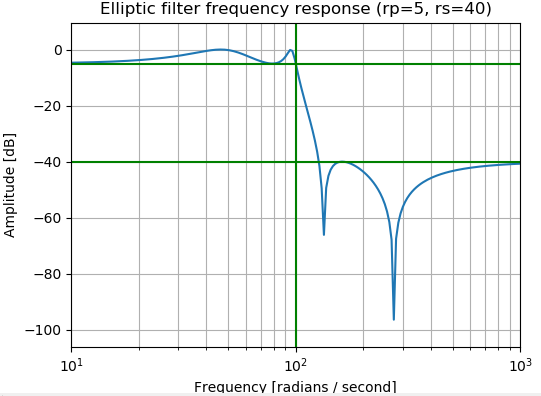
下采样方法
插值方法进行下采样
Volodymyr Kuleshov的论文中使用抗混叠滤波器对语音信号进行下采样,再通过三次样条插值把下采样信号上采样到相同的长度。
from scipy.signal import decimate import librosa import numpy as np import matplotlib.pyplot as plt from scipy import interpolate def upsample(x_lr, r): """ 上采样,每隔一步去掉语音波形的r个点,然后用三次样条插值的方法把去掉的点补回来,有机会可以画图看看 :param x_lr: 音频数据 :param r: 样条插值前个数 :return: 样条插值后的音频信号 """ x_lr = x_lr.flatten() # 把x_lr数组折叠成一维的数组 x_hr_len = len(x_lr) * r i_lr = np.arange(x_hr_len, step=r) i_hr = np.arange(x_hr_len) f = interpolate.splrep(i_lr, x_lr) # 样条曲线插值系数 x_sp = interpolate.splev(i_hr, f) # 给定样条表示的节点和系数,返回在节点处的样条值 return x_sp yt, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) x_lr = decimate(yt, 2) # 应用抗混叠滤波器后对信号进行下采样,获得低分辨率音频,下采样因子scale=2 print(len(yt)) print(len(x_lr)) plt.subplot(2, 1, 1) plt.specgram(yt, Fs=16000, scale_by_freq=True, sides='default') x_lr = upsample(x_lr, 2) # 上采样 plt.subplot(2, 1, 2) plt.specgram(x_lr, Fs=16000, scale_by_freq=True, sides='default') plt.show()
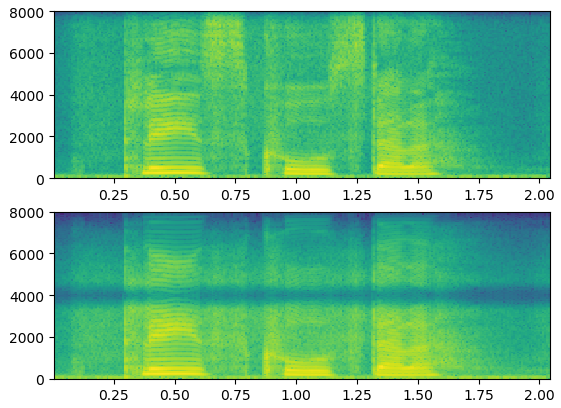
重采样(signal.resample)——下采样
利用重新采样的方法对语音进行下采样
scipy.signal.resample(x, num, t=None, axis=0, window=None)
沿给定轴使用傅立叶方法重新采样x到num个样本。因为使用傅立叶方法,所以假设信号是周期性的。
参数:
- x:要重采样的数组
- num:重采样信号的样本数
返回:
- resample_x:重新采样返回的数组
import librosa from scipy import signal import numpy as np import matplotlib.pyplot as plt y, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) f = signal.resample(y, len(y)//2) f = signal.resample(f, len(y)) plt.subplot(2,1,1) plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default') plt.subplot(2,1,2) plt.specgram(f, Fs=16000, scale_by_freq=True, sides='default') plt.show()
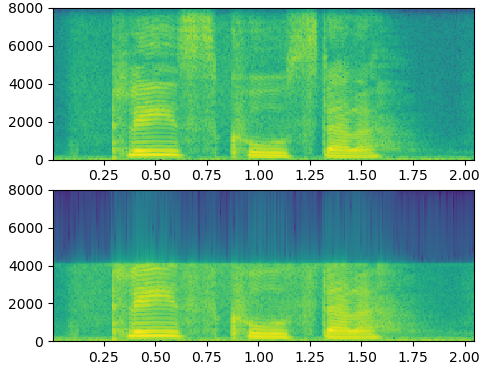
librosa.core.resample重采样(下采样)
凌振华老师的下采样方法和上面的一样
import librosa from scipy import signal import numpy as np import matplotlib.pyplot as plt y, wav_fs = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) audio8k = librosa.core.resample(y, wav_fs, wav_fs/2) # 下采样率 16000-->8000 audio8k = librosa.core.resample(audio8k, wav_fs/2, wav_fs) # 上采样率 8000-->16000,并不恢复高频部分 plt.subplot(2,1,1) plt.specgram(y, Fs=16000, scale_by_freq=True, sides='default') plt.subplot(2,1,2) plt.specgram(audio8k, Fs=16000, scale_by_freq=True, sides='default') plt.show()
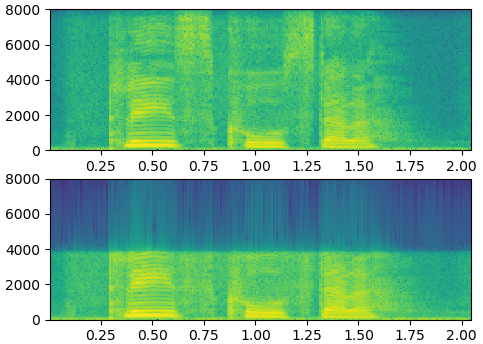
librosa.load下采样
用librosa.load想下采样,再不恢复频率的情况下上采样。
import librosa import matplotlib.pyplot as plt y_16k, fs_16k = librosa.load("./48k/p225_001.wav", sr=16000, mono=True) y_8k, fs_8k = librosa.load("./48k/p225_001.wav", sr=8000, mono=True) librosa.output.write_wav('./8k_sample.wav', y_8k, sr=8000) # 把下采样的写好 y_8k, fs_8k = librosa.load("./8k_sample.wav", sr=16000, mono=True) # 失去的就补不回来了 plt.subplot(2, 1, 1) plt.specgram(y_16k, Fs=16000, scale_by_freq=True, sides='default') plt.xlabel('16k') plt.subplot(2, 1, 2) plt.specgram(y_8k, Fs=16000, scale_by_freq=True, sides='default') plt.xlabel('8k') plt.show()