K近邻算法
1 模型建立的基本思路
学习机器学习,永远是从分类模型开始——这是一种有监督的,最容易理解的机器学习模型。分类算法是根据样本的特征预测出样本所在的类别,因此分类算法中的标签的类别通常使用整数来表示。例如,如果只有两种类别:男女,是否,正负,则我们往往使用0表示一类,1表示一类,或者使用 [1,-1]分别表示两类。当分类的标签中含有多种类别,比如说“哺乳动物,软体动物,节肢动物”,则我们通常将标签表示为0,1,2。理论上来说,表示为10,20,30也是没什么问题的,但行业惯例是将类别表示为从0开始的整数。
对于分类模型,我们首先需要给模型输入一组包含特征和标签的数据,计算机会依据算法的引导从这组数据中进行学习,并逐渐形成我们所需要的模型。这个过程叫做训练,这一组被导入的数据叫做训练集。学习完毕后,模型就建成了,此时我们导入另一组数据,但这组数据中只有特征,没有标签。模型会帮我们预测出这组数据的预测标签,我们则需要对比预测出来的标签和这组特征所对应的真正的标签的差异。差异越小,证明模型的效果越好。
在这个流程中,要求我们将数据分解为训练集和测试集。几乎所有的分类算法原理,都是关于模型如何在训练集上进行学习的过程。越复杂的模型,这个学习过程越难,当学习过程变得逐渐复杂,模型也会逐渐趋向于不可解释。因此,简单而有效的模型是机器学习界的珍宝。
2 KNN原理基础
KNN(K-Nearest Neighbour algorithm),又称为K近邻算法,是数据挖掘技术中原理最简单的算法之一。KNN的核心功能是解决有监督的分类问题,但也可以被用于回归之中。作为惰性学习算法,KNN不产生模型,因此算法准确性并不具备强可推广性,但KNN能够快速高效地解决建立在特殊数据集上的预测分类问题,因此其具备非常广泛的使用情景。在说KNN的原理之前我们来看看下面的这两个问题:
样本 x 应该属于哪个类?
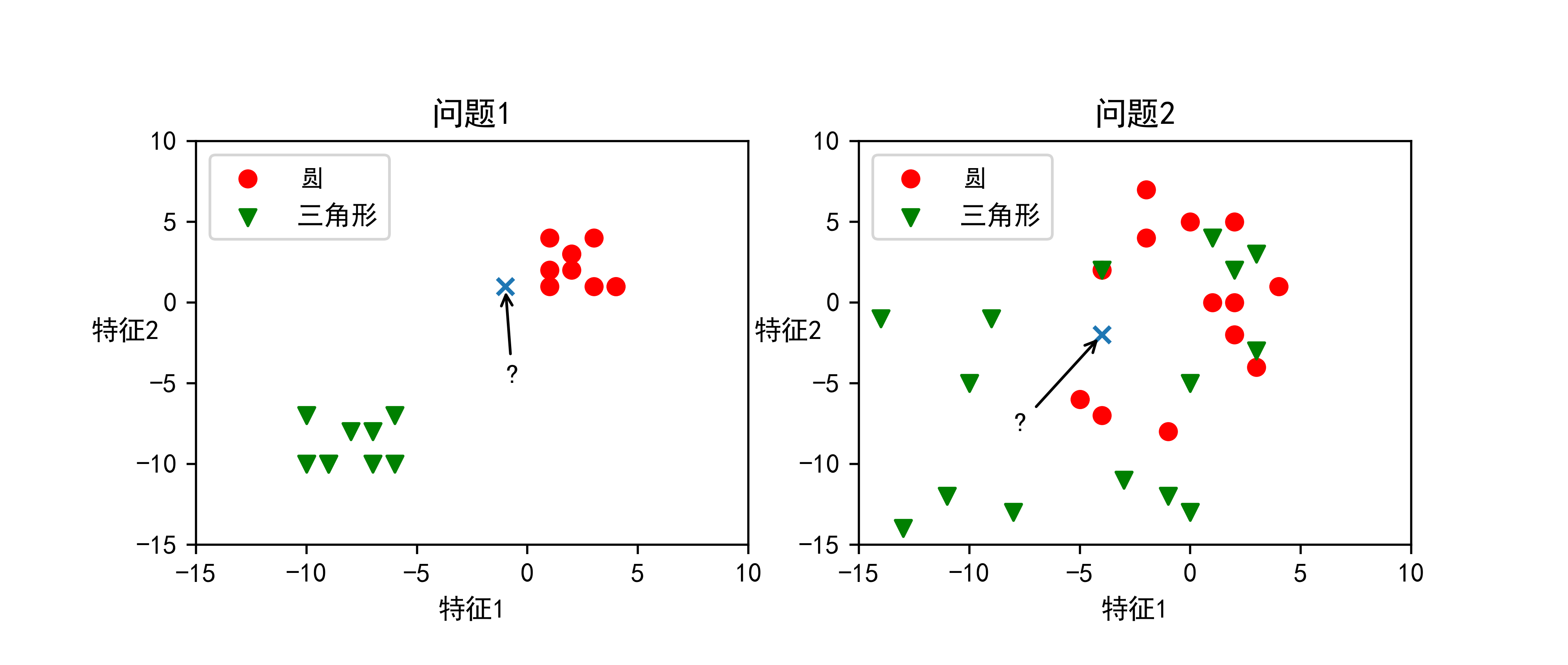
对于这样的两个问题:
第一个问题, 我想我们每个人都会把x分成圆这样一类, 那么为什么呢?
第二个问题, x又该属于哪个类呢?
对于第二个问题,我们很难有什么好的理由简单的判别x是属于哪个类, 既然如此, 我们来看看KNN是如何解决这个问题的。
KNN的算法原理:一个数据集中存在多个已有标签的样本值,这些样本值共有的n个特征构成了一个多维空间N。当有一个需要预测/分类的样本x出现时,我们把这个x放到多维空间n中,找到离其距离最近的k个样本,并将这些样本称为最近邻(nearest neighbour)。对这k个最近邻,查看他们的标签都属于何种类别,根据”少数服从多数,一点算一票”的原则进行判断,数量最多标签类别就是x的标签类别。其中涉及到的原理是“越相近越相似”,这也是KNN的基本假设。
如果还没明白, 也没有关系, 我们再来看看下面这些图:
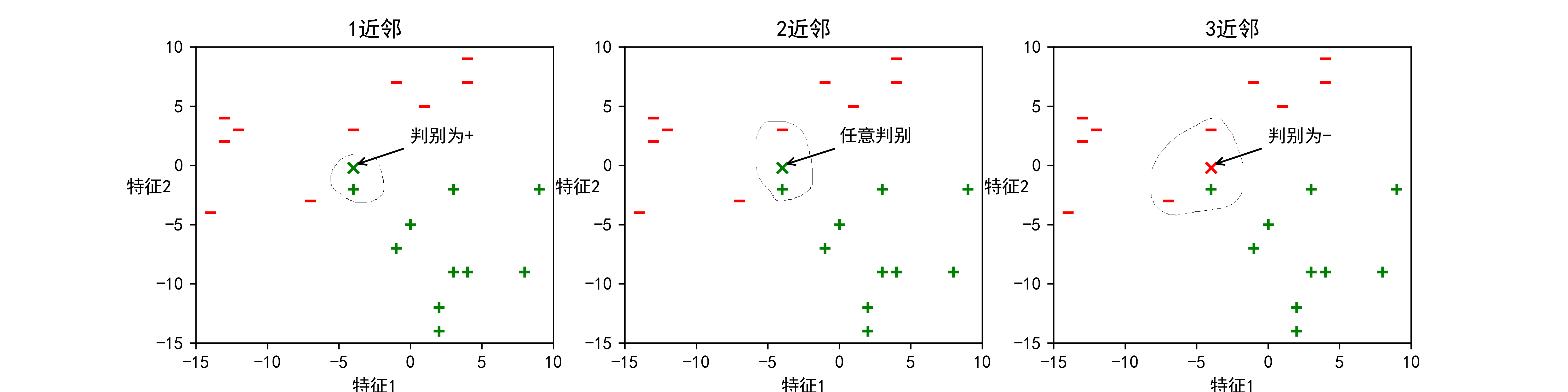
上面的数据集只有两个特征,则针对于数据集的描述可用二维平面空间图来表示。如下图,二位平面空间
由上可知,KNN算法的实现步骤其实非常简单,假设现在我们有一个预测样本X,则判断X的分类的方法为:
1. 计算X到所有训练集上的点的距离
2. 按照距离递增次序对样本点进行排序
3. 取前K个离X最近的点,查看他们的标签
4. 对这K个点的标签分类计数,采取少数服从多数策略,占多数的标签则为点X的预测标签
由此可见KNN的几个关键问题:
-
如何衡量距离, 或者说用什么来衡量最近?
-
k到底应该选择多少?
-
最后的决策规则
2.1 距离类模型的度量
在距离类模型,例如KNN中,有多种常见的距离衡量方法。大多数时候我们使用的是数据距离,又以 欧几里得距离为最常见。
-
欧几里得距离
对于数据之间的距离而言,在欧式空间中我们常常使用欧几里得距离,也就是我们常说的距离平方和开平方。回忆一下,一个平面直角坐标系上,如何计算两点之间的距离?一个立体直角坐标系上,又如何计算两点之间的距离?
在n维空间中,有两个点A和B,两点的坐标分别为:
则A和B两点之间的欧几里得距离的基本计算公式如下:
而在我们的机器学习中,坐标轴上的值正是我们样本数据上的n个特征。
-
曼哈顿距离
曼哈顿距离,也被称作街道距离,该距离用以标明两个点在标准坐标系上的绝对轴距总和,其计算方 法相当于是欧式距离的1次方表示形式,其基本计算公式如下:
-
闵科夫斯基距离
无论是欧式距离还是曼哈顿距离,都可视为闵可夫斯基距离的一种特例,该距离计算公式如下:
当p=1时,为曼哈顿距离
当p=2时,为欧式距离
当p趋于无穷时,为切比雪夫距离
-
夹角余弦
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个样本差异的大小。余弦值越接近1, 说明两个向量夹角越接近0度,表明两个向量越相似。其计算方法如下:
但是在KNN中,几乎默认使用欧几里得距离。
2.2 Python手动实现KNN
2.2.1 构建原始数据集
为了方便验证,这里使用python的字典dict构建数据集,然后再将其转化成DataFrame格式。
# 导入相关包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
plt.style.use('seaborn')
plt.rcParams['font.sans-serif']=['Simhei'] #显示中文
plt.rcParams['axes.unicode_minus']=False #显示负号
# 创建原始的数据
# 创建原始数据集
data={'电影名称':['无问西东','后来的我们','前任3','红海行动','唐人街探案','战狼2'],
'打斗镜头':[1,5,12,108,112,115],
'接吻镜头':[101,89,97,5,9,8],
'电影类型':['爱情片','爱情片','爱情片','动作片','动作片','动作片']}
# 数据读成DataFrame类型
df_data = pd.DataFrame(data)
df_data
2.2.2 原始数据集可视化
# 将电影的类型映射成颜色, 以便在散点图中区别
df_data['颜色'] = df_data.电影类型.map({'爱情片':'r', '动作片':'g'})
df_data
# 创建画布
plt.figure(figsize=(8, 6), dpi=70)
# 数据分布
plt.scatter(x=df_data.打斗镜头, y=df_data.接吻镜头, color=df_data.颜色, marker='*');
# 要预测的点
plt.scatter(24, 67)
# 其他图像设置
plt.xlabel('打斗镜头', fontsize=15)
plt.ylabel('接吻镜头', rotation=0, fontsize=15)
plt.title('电影分类', fontsize=20)
plt.annotate("要预测这个点应该是什么颜色?", (24, 67), (50, 60), arrowprops=dict(arrowstyle="->"), fontsize=15)
plt.savefig('a10.jpg', dpi=500);
2.2.3 KNN算法流程
2.2.3.1 计算预测点[24, 67]到所有样本的距离
# 添加一列每个样本到预测点的距离
df_data['到预测点的距离'] = ((df_data.打斗镜头-24)**2+(df_data.接吻镜头-67)**2)**0.5
df_data
2.2.3.2 按照距离进行升序, 并选取距离最小的k=4个
# 这里我们去k=4
df_data.sort_values('到预测点的距离')[0:4]
2.2.3.3 查看上表的电影类型的计数, 取最高的类别, 即为该预测点的类别
# Series对象的value_counts()方法对每个值进行计数统计
df_data.sort_values('到预测点的距离')[0:4].电影类型.value_counts().index[0]
#最后输出:
# '爱情片'
2.2.3.4 将上诉过程封装成一个函数
def knn(new_data, data_df, k):
'''
函数功能:KNN分类器
参数说明:
new_data:要预测的点, 接受一个列表或者元祖
data_df :训练集
k :k近邻算法的前k个距离最近的点
返回值:
该预测点的分类结果
'''
df_data['到预测点的距离'] = ((df_data.打斗镜头-new_data[0])**2+(df_data.接吻镜头- new_data[1])**2)**0.5
a = df_data.sort_values('到预测点的距离')[0:k]
return a.电影类型.value_counts().index[0]
# 调用函数
knn(new_data, df_data, 4)
# 输出:
# '爱情片'
2.3 使用sklearn实现KNN
我们已经手动实现了KNN算法,并且获得了意料之中的结果。但大家可能发现,在整个建模过程中,我们刚才的函数只实现了算法原理这一小部分,还剩下一堆的:划分训练集和测试集,进行测试,评估模型等过程,都没有进行手写。实际上,如果这些代码全部都要手敲的话,整个KNN大概是需要200行左右的。作为机器学习中最简单的算法尚且如此,更不要说原理复杂得多的算法们了,因此实际上,大多数时候我们是不会手敲代码的。相对的,我们使用自带一系列算法的算法库:sklearn来帮助我们。
scikit-learn,又写作sklearn,是一个开源的基于python语言的机器学习工具包。它通过NumPy, SciPy 和Matplotlib等python数值计算的库实现高效的算法应用,并且涵盖了几乎所有主流机器学习算法。
http://scikit-learn.org/stable/index.html
在工程应用中,用python手写代码来从头实现一个算法的可能性非常低,这样不仅耗时耗力,还不一定能够写出构架清晰,稳定性强的模型。更多情况下,是分析采集到的数据,根据数据特征选择适合的算法,在工具包中调用算法,调整算法的参数,获取需要的信息,从而实现算法效率和效果之间的平衡。而sklearn,正是这样一个可以帮助我们高效实现算法应用的工具包。
其实现代码的过程异常简单,就刚才我们所写的knn函数,在sklearn中仅需要四行就可以。我们先来看看sklearn的一般建模流程:
在这个流程下,KNN对应的代码是:
# 从sklearn.neighbors里导入 KNN分类器的类 from sklearn.neighbors import KNeighborsClassifier # 通过类实例化一个knn分类器对象 # 类中的具体参数 # KNeighborsClassifier(n_neighbors=5,weights='uniform',algorithm='auto',leaf_size=30,p=2, # metric='minkowski',metric_params=None,n_jobs=None,**kwargs,) knn_clf = KNeighborsClassifier(n_neighbors=k) # 通过对象调fit()方法, 传入训练集, 训练模型 knn_clf.fit(x_train, y_train) # 训练好的模型, 通过其他接口, 传入测试集查看模型效果 knn_clf.score(x_test, y_test)
其中参数n_neighbors就是我们的参数K:最近的K个点。 我们可以试试看刚才的电影数据集:
2.3.1 首先给我们的数据集加一列数字标签
# 我们要求预测的是这个电影类型, 但是现在电影类型 爱情片 动作片是文本型
# 但是在算法里要求是数值型, 于是, 我们用0表示爱情片, 1表示动作片
df_data['标签'] = df_data.电影类型.map({'爱情片':0, '动作片':1})
df_data
2.3.2 提取 训练集 的 特征 和 标签
一般而言, 在sklearn, 我们通过fit(X,y)进行训练的时候, 特征X通常需要接受一个二维的数组或者DataFrame, 标签y通常接受一维的数组或者Series对象。
# 提取训练集的特征 x_train = df_data.loc[:, ['打斗镜头', '接吻镜头']] # 提取训练集的标签 y_train = df_data['标签']
2.3.3 训练模型
# 导入KNN分类器的类 from sklearn.neighbors import KNeighborsClassifier # 实例化一个knn分类器对象, 采取5个最近邻 knn_clf = KNeighborsClassifier(n_neighbors=5) # .fit(X, y)分别接受训练集的特征和标签 knn_clf.fit(x_train,y_train)
2.3.4 传入测试集查看结果
# .predict()接口, 返回类别标签 knn_clf.predict([[24, 57]]) # array([0], dtype=int64) , 告诉我们这个点是0类 # .predict_proba接口返回分别属于0类, 1类, 2类...的概率 knn_clf.predict_proba([[24, 57]]) # array([[0.6, 0.4]]) # 告诉我们, 这个点属于0类的概率是0.6, 属于1类的概率是0.4 # .score(x_test, y_test), 返回的是准确率 knn_clf.score([[24, 67]], [0]) # 1.0
这就是如何使用KNN进行建模的步骤, 当然, 我们这里的数据集太简单了, 我们来一个比较大的数据集。在sklearn里面已经给我们内置了许多数据集。
https://scikit-learn.org/stable/modules/classes.html#module-sklearn.datasets
3 KNN实战乳腺癌数据集
# 导入KNN的类 from sklearn.neighbors import KNeighborsClassifier # 导入乳腺癌数据集 from sklearn.datasets import load_breast_cancer # 导入划分测试集和训练集的工具 from sklearn.model_selection import train_test_split
3.1 提取数据中的特征和标签
# 提取数据集
data = load_breast_cancer()
# sklearn里面的数据集返回的是一个字典
# 'data'对应的是特征, 'target'的标签, 'target_names'对应的是类别的名称
# 'feature_names'对应的是每一列的名字
data
# 提取特征, 返回的是一个二维数组
X = data['data']
# 通常, 习惯上我们喜欢将其转化为DataFrame,然后重新给每列加上列名
X = pd.DataFrame(X)
X.columns = name = ['平均半径','平均纹理','平均周长','平均面积',
'平均光滑度','平均紧凑度','平均凹度',
'平均凹点','平均对称','平均分形维数',
'半径误差','纹理误差','周长误差','面积误差',
'平滑度误差','紧凑度误差','凹度误差',
'凹点误差','对称误差',
'分形维数误差','最差半径','最差纹理',
'最差的边界','最差的区域','最差的平滑度',
'最差的紧凑性','最差的凹陷','最差的凹点',
'最差的对称性','最差的分形维数']
X
# 提取标签
y = data['target']
3.2 划分测试集和训练集
# 可查看用法 train_test_split? # 划分测试集和训练集 #按照训练集占70%, 测试集占30%划分, 随机划分的方式可以设置, 保证下次划分的结果和此次一次 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) X_train.shape y_train.shape X_test.shape y_test.shape
3.3 建立模型与模型评估
# 实例化一个5个最近邻的knn分类器 knn_clf = KNeighborsClassifier(n_neighbors=5) # 训练模型 knn_clf.fit(X_train, y_train) # 测试模型的准确率 knn_clf.score(X_test, y_test) # 0.9590643274853801
我们这里的最近邻k, 选取的是5, 得到的模型的准确率大概在0.96左右, 我们知道的是, 随着k的选择的不同, 结果肯定会不一样, 那么k到底该选哪个更合适呢?
4 模型调参
4.1 学习曲线
KNN中的K是一个超参数,所谓“超参数”,就是需要人为输入,算法不能通过计算得出的参数。KNN中的K代表的是距离需要分类的测试点x最近的K个样本点,如果不输入这个值,KNN算法中的重要部分“选出K个最近邻”就无法实现。从KNN的原理中可见,是否能够确认合适的k值对算法有极大的影响。如果K太小,则最近邻分类器容易受到由于训练数据中的噪声而产生的过分拟合的影响;相反。如果k太大,最近邻分类器可能会将测试样例分类错误,因为k个最近邻中可能包含了距离较远的,并非同类的数据点。因此,超参数K的选定是KNN中的头号问题。
那我们怎样选择一个最佳的K呢?在这里我们要使用机器学习中的神器:参数学习曲线。参数学习曲线是一条以不同的参数取值为横坐标,不同参数取值下的模型结果为纵坐标的曲线,我们往往选择模型表现最佳点的参数取值作为这个参数的取值。比如我们的乳腺癌数据集:我们让k从1-20, 可以返回20个准确率, 使得准确率最高的那个k就是我们要的。
L = []
for k in range(1, 21):
knn_clf = KNeighborsClassifier(n_neighbors=k)
knn_clf.fit(X_train, y_train)
L.append((k, knn_clf.score(X_test, y_test)))
L
# 将结果转化为DataFrame
score = pd.DataFrame(L)
score.columns = ['k', '准确率']
score
画k值得学习曲线:
# 画学习曲线
plt.figure(figsize=(8, 6), dpi=100)
plt.plot(score.k, score.准确率)
plt.annotate("最高的准确率", (10, 0.982456), (14, 0.978), arrowprops=dict(arrowstyle="->"))
plt.xticks(score.k)
plt.xlabel('k值', fontsize=20)
plt.ylabel('准确率', fontsize=20)
plt.savefig('学习曲线.png', dpi=350)
plt.title("k值学习曲线")
plt.show();
用这样的方式我们就找出了最佳的K值——这体现了机器学习当中,一切以“模型效果”为导向的性质,我们可以使用模型效果来帮助我们选择参数。
4.2 交叉验证
好像到这里, 我们已经大功告成了, 我们可以通过学习曲线找出最优的k, 看上去是如此的简单优雅, 但是, 上帝总会在天空是给你飘几朵乌云...请看下面的代码:
# 这里划分测试集和训练集的时候, 我们不要指定随机方式, 让每次划分的训练集和测试集不一样
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
L = []
for k in range(1, 21):
knn_clf = KNeighborsClassifier(n_neighbors=k)
knn_clf.fit(X_train, y_train)
L.append((k, knn_clf.score(X_test, y_test)))
score = pd.DataFrame(L)
score.columns = ['k', '准确率']
# 画学习曲线
plt.figure(figsize=(8, 6), dpi=100)
plt.plot(score.k, score.准确率)
plt.xticks(score.k)
plt.xlabel('k值', fontsize=20)
plt.ylabel('准确率', fontsize=20)
plt.savefig('学习曲线.png', dpi=350)
plt.title("k值学习曲线")
plt.show();
你发现了什么?每次运行的时候学习曲线都在变化,模型的效果时好时坏,这是为什么呢?实际上,这是由于训练集和测试集的划分不同造成的。每次都使用不同的训练集进行训练,不同的测试集进行测试,自然也就会有不同的模型结果。在业务当中,我们的训练数据往往是已有的历史数据,但我们的测试数据却是新进入系统的一系列还没有标签的数据。我们的确追求模型的效果,但我们追求的是模型在未知数据集上的效果,在陌生数据集上表现优秀的能力被成为泛化能力,即我们追求的是模型的泛化能力。
我们认为,如果模型在一套训练集和数据集上表现优秀,那说明不了问题,只有在众多不同的训练集和测试集上都表现优秀,模型才是一个稳定的模型,模型才具有泛化能力。为此,机器学习领域有着发挥神作用的技能:交叉验证,来帮助我们认识模型。
最简单的交叉验证叫做K折交叉验证。我们将数据划分为n份,依次使用其中一份作为测试集,其他n-1份作为训练集,这样就会出现n个准确率, 我们再对这n个准确率求平均值。如果平均准确率高的, 就说明泛化能力更强。
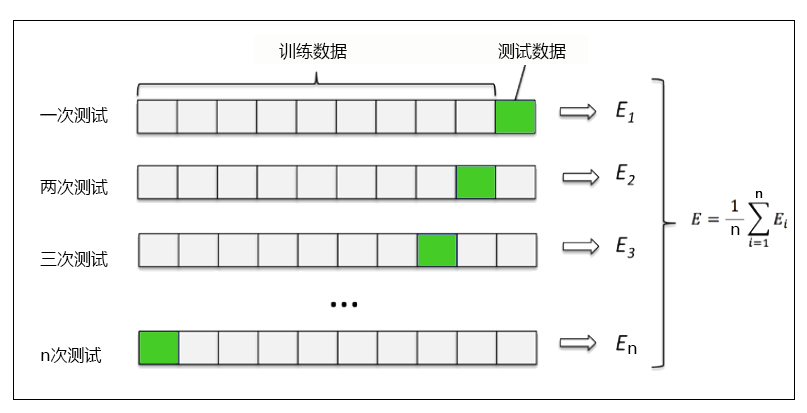
当然, 幸运的是, sklearn里面同样为我们提供了交叉验证的类cross_val_score
# 导入交叉验证的类
from sklearn.model_selection import cross_val_score
cross_val_score?
# 导入交叉验证的类
knn3_clf = KNeighborsClassifier(n_neighbors=3) # k=3
result = cvs(knn3_clf, # 已经实例化好了的一个, 还没有进行训练的模型
X, # 输入没有进行划分的数据的特征
y, # 输入没有进行划分的数据的标签
cv = 5) # 输入交叉验证的折数
result
# array([0.87826087, 0.92173913, 0.94690265, 0.9380531 , 0.91150442])
# 均值:查看模型的平均效果
result.mean() # 0.9192920353982302
# 方差:查看模型的稳定性
result.var() # 0.0005729030951466963
也就是说, 通过5折交叉验证, 我们看见在k=3的KNN的平均准确率是0.92左右,现在判断一个模型好不好, 不仅要求其平均准确率高, 好要求模型稳定也就是方差要较小。
绘制带5折交叉验证的学习曲线
L = []
for k in range(1, 21):
knn_clf = KNeighborsClassifier(n_neighbors=k)
result = cvs(knn_clf, # 已经实例化好了的一个, 还没有进行训练的模型
X, # 输入没有进行划分的数据的特征
y, # 输入没有进行划分的数据的标签
cv = 5) # 输入交叉验证的折数
result_mean = result.mean()
result_var = result.var()
L.append((k, result_mean, result_var))
score = pd.DataFrame(L)
score.columns = ['k', '平均准确率', '方差']
score
# 画学习曲线
plt.figure(figsize=(8, 6), dpi=100)
plt.plot(score.k, score.平均准确率)
# 再画两条偏离均值2倍方差的曲线
plt.plot(score.k, score.平均准确率+2*score.方差, linestyle='--', color='r')
plt.plot(score.k, score.平均准确率-2*score.方差, linestyle='--', color='r')
plt.xticks(score.k)
plt.xlabel('k值', fontsize=20)
plt.ylabel('平均准确率', fontsize=20)
plt.savefig('带5折交叉验证的学习曲线.png', dpi=350)
plt.title("带5折交叉验证的k值学习曲线")
plt.show();
对于带交叉验证的学习曲线,我们需要观察的就不仅仅是最高的准确率了,而是准确率高,方差还相 对较小的点,这样的点泛化能力才是最强的。在交叉验证+学习曲线的作用下,我们选出的超参数能够保证更好的泛化能力。
然而交叉验证却没有这么简单。交叉验证有许多坑大家可能会踩进去,在这里给大家列举出来:
-
最标准,最严谨的交叉验证应该有三组数据:训练集,验证集和测试集。当我们获取一组数据后, 我们会先将数据集分成整体的训练集和测试集,然后我们把训练集放入交叉验证中,从训练集中分割出更小的训练集(n-1份)和验证集(1份),此时我们返回的交叉验证结果其实是验证集上的结果。我们使用验证集寻找最佳参数,确认一个我们认为泛化能力最佳的模型,然后我们将这个模型使用在测试集上,观察模型的表现。通常来说,我们认为经过验证集找出最后参数后的模型的泛化能力是增强了的,因此模型在未知数据(测试集)上的效果会更好,但尴尬的是,模型经过交叉验证在验证集上的调参之后,在测试集上的结果没有变好的情况时有发生。原因其实是:我们自己分的测试集和训练集,会影响模型的结果,同时,交叉验证后的模型泛化能力增强了,表示它在未知数据集上方差更小,平均水平更高,但却无法保证它在现在分出来的测试集上预测能力最强——如此说来,是否有测试集的存在,其实意义不大了。如果我们相信交叉验证的调整结果是增强了模型的泛化能力的,那即便测试集上的测试结果并没有变好(甚至变坏了),我们也认为模型是成功的,如果我们不相信交叉验证的调整结果能够增强模型的泛化能力,而一定要依赖于测试集来进行判断,我们完全没有进行交叉验证的必要,直接用测试集上的结果来跑学习曲线就好了。所以,究竟是否需要验证集,其实是存在争议的,在严谨的情况下,大家还是要使用有验证集的方式。即:要先划分测试集和训练集。
-
交叉验证方法不止K折一种,分割训练集和测试集的方法也不止一种,分门别类的交叉验证占据了sklearn中非常长的一章:https://scikit-learn.org/stable/modules/cross_validation.html。
所有的交叉验证都是在分割训练集和测试集,只不过侧重的方向不同,像K折法就是按顺序取训练集和测试集,ShuffleSplit就侧重于让测试集分布在数据的全方位之内,StratifiedKFold则是认为训练数据和测试数据必须在每个标签分类中占有相同的比例。各类交叉验证的原理繁琐,大家在机器学习道路上一定会逐渐遇到更难的交叉验证,但是万变不离其宗:本质交叉验证是为了解决分训练集和测试集对模型带来的影响,同时检测模型的泛化能力的。
![]()
![]()
![]()
具体中文文档可参考:https://sklearn.apachecn.org/docs/0.21.3/30.html
-
K折交叉验证对数据的分割方式是按顺序的,因此在使用交叉验证之前需要排查数据的标签本身是否有顺序,如果有顺序则需要打乱原有的顺序,或者更换交叉验证方法,像ShuffleSplit就完全不在意数据本身是否是有顺序的。
关于交叉验证的思考:我们说交叉验证是为了提高模型的泛化能力, 使其在未知数据集上表现也会不错, 那么为什么我们模型的泛化能力会不够呢?归根到底还是数据量太少,我们拿到的数据根本不足以说明整个情况 , 这就导致很多为难的情况, 如果我们把训练集拟合的足够好,但是如果训练集本身没有包含整体情况的多数信息, 当我们把这个模型运用到未知的数据集上时, 效果往往是不好的, 这就是机器学习中常说的过拟合(overfitting):即模型在训练集上很好, 但在测试集上表现很差, 与之相对的就有欠拟合(underfitting), 即模型的对数据的拟合能力不足。所以, 一个模型的能力要想够好, 训练数据一定会非常非常大才行。
5 KNN中距离的讨论
在乳腺癌数据集上我们发现,5折交叉验证的情况下, 模型的结果最好也就是大约93%左右,如果我们希望继续提升模型效果, 怎么做呢?来看下面这一段代码:
# 导入数据归一化的包
from sklearn.preprocessing import MinMaxScaler as mms
# 对特征进行数据归一化
X_ = mms().fit_transform(X)
L = []
for k in range(1, 21):
knn_clf = KNeighborsClassifier(n_neighbors=k)
result = cvs(knn_clf, # 已经实例化好了的一个, 还没有进行训练的模型
X_, # 输入没有进行划分的数据的特征
y, # 输入没有进行划分的数据的标签
cv = 5) # 输入交叉验证的折数
result_mean = result.mean()
result_var = result.var()
L.append((k, result_mean, result_var))
score = pd.DataFrame(L)
score.columns = ['k', '平均准确率', '方差']
score
# 画学习曲线
plt.figure(figsize=(8, 6), dpi=100)
plt.plot(score.k, score.平均准确率)
# 再画两条偏离均值2倍方差的曲线
plt.plot(score.k, score.平均准确率+2*score.方差, linestyle='--', color='r')
plt.plot(score.k, score.平均准确率-2*score.方差, linestyle='--', color='r')
plt.xticks(score.k)
plt.xlabel('k值', fontsize=20)
plt.ylabel('平均准确率', fontsize=20)
#plt.savefig('带5折交叉验证的学习曲线.png', dpi=350)
plt.title("带5折交叉验证的k值学习曲线")
plt.show();
你发现了什么?模型的效果很快就上升了,而我只增加了两行代码:
# 导入数据归一化的包 from sklearn.preprocessing import MinMaxScaler as mms # 对特征进行数据归一化 X_ = mms().fit_transform(X)
5.1 距离类模型的归一化需求
什么是归一化呢?我们看看X与归一化后的X_有什么区别:
原来的数据有些很大, 有些很小, 这种情况在机器学习中被称为——量纲不统一, KNN是距离类模型,欧式距离的计算公式中存在着特征上的平方和:
试想看看,如果某个特征的取值非常大,其他特征的取值和它比起来都不算什么,那距离的大小很大程度上都会由这个巨大特征来决定,其他的特征之间的距离可能就无法对的大小产生什么影响了,这种现象会让KNN这样的距离类模型的效果大打折扣。然而在实际分析情景当中,绝大多数数据集都会存在各特征值量纲不同的情况,此时若要使用KNN分类器,则需要先对数据集进行归一化处理,即是将所有的数据压缩到同一个范围内。数据的归一化或者标准化, 主要目的是消除量纲对距离类模型的影响,还有就是加速梯度下降等算法的迭代速度,使其更快找到最优解。
-
preprocessing.MinMaxScaler
当数据(x)按照最小值中心化后,再按极差(最大值 - 最小值)缩放,数据移动了最小值个单位,并且会 被收敛到[0,1]之间,而这个过程,就叫做数据归一化(Normalization,又称Min-Max Scaling)。注意Normalization是归一化,不是正则化,真正的正则化是regularization,不是数据预处理的一种手段。 0-1归一化的公式如下:
在sklearn当中,我们使用preprocessing.MinMaxScaler来实现这个功能。MinMaxScaler有一个重要 参数,feature_range,控制我们希望把数据压缩到的范围,默认是[0,1]。
# 导入归一化的类 from sklearn.preprocessing import MinMaxScaler # 实例化一个归一化对象, 默认归一到(0-1)之间 mms = MinMaxScaler() data = np.array([[-1, 2], [-0.5, 6], [0, 10], [1, 18]]) data
# .fit()这一步相当于是找到data里面的最大值max(x)和最小值min(x) mms.fit(data) # .transform()相当于导出最后的归一化结果 mms.transform(data) # 还有一种一步到位的方式 mms.fit_transform(data)
思考:先切分训练集和测试集,还是先进行归一化?
学会了归一化的类之后,来看看正确的归一化流程。最初的时候,为了让大家能够最快地看到模型的效果变化,我直接在全数据集X上进行了归一化,然后放入交叉验证绘制学习曲线,这种做法是错误的,只是为了教学目的方便才这样操作。真正正确的方式是,先分训练集和测试集,再归一化!
为什么呢?想想看归一化的处理手段,我们是使用数据中的最小值和极差在对数据进行压缩处理,如果我们在全数据集上进行归一化,那最小值和极差的选取是会参考测试集中的数据的状况的。因此,当我们归一化之后,无论我 们如何分割数据,都会由一部分测试集的信息被“泄露”给了训练集(当然,也有部分训练集的信息被泄露给了测试集,但我们不关心这个),这会使得我们的模型效果被高估。
在现实业务中,我们只直到训练集的数据,不了解测试集究竟会长什么样,所以我们要利用训练集上的最小值和极差来归一化测试集。正确的操作是这样的:
# 先划分测试集和训练集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 导入归一化类
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler() # 实例化对象
mms.fit(X_train) # 这一步是在学习训练集,生成训练集上的极小值和极差
X_train = mms.transform(X_train) # 用训练集上的极小值和极差归一化训练集
X_test = mms.transform(X_test) # 用训练集上的极小值和极差归一化测试集
# 重新建模找k
from sklearn.model_selection import cross_val_score as csv
L = []
for k in range(1, 21):
knn_clf = KNeighborsClassifier(n_neighbors=k)
result = cvs(knn_clf, # 已经实例化好了的一个, 还没有进行训练的模型
X_train, # 使用训练集
y_train,
cv = 5) # 5折交叉验证
result_mean = result.mean()
result_var = result.var()
L.append((k, result_mean, result_var))
score = pd.DataFrame(L)
score.columns = ['k', '平均准确率', '方差']
# 画学习曲线
plt.figure(figsize=(8, 6), dpi=100)
plt.plot(score.k, score.平均准确率)
# 再画两条偏离均值2倍方差的曲线
plt.plot(score.k, score.平均准确率+2*score.方差, linestyle='--', color='r')
plt.plot(score.k, score.平均准确率-2*score.方差, linestyle='--', color='r')
plt.xticks(score.k)
plt.xlabel('k值', fontsize=20)
plt.ylabel('平均准确率', fontsize=20)
plt.title("k值学习曲线")
#plt.savefig('训练.png', dpi=350)
plt.show();
观察, 我们发现, 在k=15的时候, 准确率最高, 还是试试其他的为准。
from sklearn.neighbors import KNeighborsClassifier # 实例化一个k=15的看看 KNN_clf = KNeighborsClassifier(n_neighbors=15) KNN_clf.fit(X_train, y_train) KNN_clf.score(X_train, y_train) KNN_clf.score(X_test, y_test) # 0.9723618090452262 # 0.9532163742690059
5.2 以距离作为惩罚因子的优化
用最近邻点距离远近修正在对未知点分类过程中“一点一票”的规则是KNN模型优化的一个重要步骤。也就是说,对于原始分类模型而言,在选取最近的K个元素之后,将参考这些点的所属类别,并对其进行简单计数,而在计数的过程中这些点“一点一票”,这些点每个点对分类目标点的分类过程中影响效力相同。
但这实际上是不公平的,就算是最近邻的K个点,每个点和分类目标点的距离仍然有远近之别,而近 的点往往和目标分类点有更大的可能性属于同一类别(注意,该假设也是KNN分类模型的基本假设)。因此,我们可以选择合适的惩罚因子,让入选的K个点在最终判别目标点属于某类别过程中发挥的作用不相同,即让相对较 远的点判别效力更弱,而相对较近的点判别效力更强。这一点也可以减少KNN算法对k取值的敏感度。
关于惩罚因子的选取有很多种方法,最常用的就是根据每个最近邻距离的不同对其作用加权,加权方法为设置 的权重,该权重计算公式为:距离的倒数
这里需要注意的是,关于模型的优化方法只是在理论上而言进行优化会提升模型判别效力,但实际应用过程中最终能否发挥作用,本质上还是取决于优化方法和实际数据情况的契合程度,如果数据本身存在大量异常值点,则采用 距离远近作为惩罚因子则会有较好的效果,反之则不然。因此在实际我们进行模型优化的过程当中,是否起到优化效果还是要以最终模型运行结果为准。
在sklearn中,我们可以通过参数weights来控制是否适用距离作为惩罚因子:
| 重要参数:weights |
|---|
| 用于决定是否使用距离作为惩罚因子的参数,默认"uniform" 可能输入的值有: "uniform":表示一点一票 "distance":表示以每个点到测试点的距离的倒数计算该点的距离所占的权重,使得距离测试点更近的样本点 比离测试点更远的样本点具有更大的影响力 |
# 加上距离惩罚性
# 先划分测试集和训练集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 导入归一化类
from sklearn.preprocessing import MinMaxScaler
mms = MinMaxScaler() # 实例化对象
mms.fit(X_train) # 这一步是在学习训练集,生成训练集上的极小值和极差
X_train = mms.transform(X_train) # 用训练集上的极小值和极差归一化训练集
X_test = mms.transform(X_test) # 用训练集上的极小值和极差归一化测试集
# 重新建模找k
from sklearn.model_selection import cross_val_score as csv
L = []
for k in range(1, 21):
knn_clf = KNeighborsClassifier(n_neighbors=k, weights='distance')
result = cvs(knn_clf, # 已经实例化好了的一个, 还没有进行训练的模型
X_train, # 使用训练集
y_train,
cv = 5) # 5折交叉验证
result_mean = result.mean()
result_var = result.var()
L.append((k, result_mean, result_var))
score = pd.DataFrame(L)
score.columns = ['k', '平均准确率', '方差']
# 画学习曲线
plt.figure(figsize=(8, 6), dpi=100)
plt.plot(score.k, score.平均准确率)
# 再画两条偏离均值2倍方差的曲线
plt.plot(score.k, score.平均准确率+2*score.方差, linestyle='--', color='r')
plt.plot(score.k, score.平均准确率-2*score.方差, linestyle='--', color='r')
plt.xticks(score.k)
plt.xlabel('k值', fontsize=20)
plt.ylabel('平均准确率', fontsize=20)
plt.title("加距离惩罚项的训练的k值学习曲线")
plt.savefig('加距离惩罚项的训练.png', dpi=350)
plt.show();
KNN = KNeighborsClassifier(n_neighbors=15, weights='distance') KNN_clf.fit(X_train, y_train) KNN_clf.score(X_train, y_train) KNN_clf.score(X_test, y_test) # 0.9773869346733668 # 0.9649122807017544
到这里,能够对KNN进行的全部优化就已经完成了。KNN代表着“投票类”的算法,一直广泛受到业界的欢迎。不过KNN也有自己的缺点,那就是它计算非常缓慢,因为KNN必须对每一个测试点来计算到每一个训练数据点的距离,并且这些距离点涉及到所有的特征,当数据的维度很大,数据量也很大的时候,KNN的计算会成为诅咒,大概几万数据就足够让KNN跑几个小时了。
无论怎样, 恭喜同学,我们就学完了KNN。


