问题描述
Sylvia 是一个热爱学习的女孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有$ n imes m $ 名学生,方阵的行数为 n,列数为 m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 $ n imes m$ 编上了号码(参见后面的样例)。即:初始时,第 i 行第 j 列 的学生的编号是 ((i-1) imes m + j)。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 q件这样的离队事件。每一次离队事件可以用数对 ((x,y) (1 le x le n, 1 le y le m)) 描述,表示第 x 行第 y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
- 向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 x 行第 m列。
- 向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 n 行第 m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n 行 第 m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
输入格式
输入共 q+1 行。
第 1 行包含 3 个用空格分隔的正整数 n, m, q,表示方阵大小是 n 行 m 列,一共发 生了 q 次事件。
接下来 q 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x, y,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 x 行第 y 列。
输出格式
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学 生的编号。
说明
【输入输出样例 1 说明】
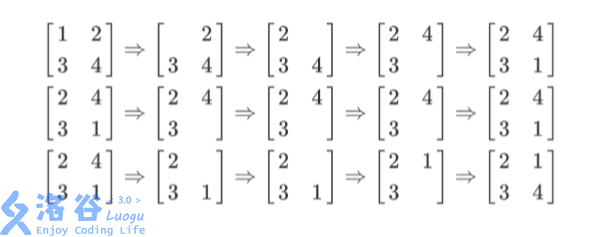
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为1 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 2 的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为4的同学向上一步,这时空位移动到第二行第二列。最后编号 为1 的同学返回填补到空位中。
【数据规模与约定】
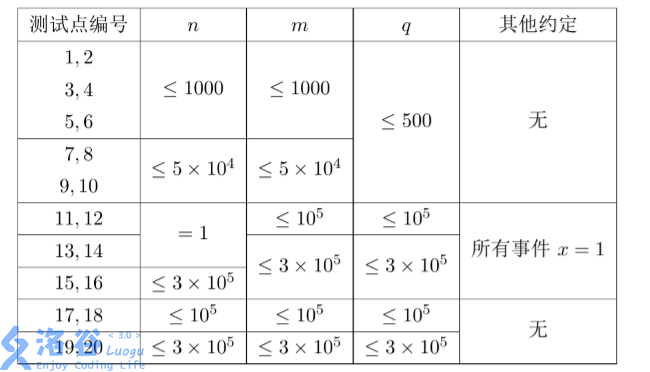
数据保证每一个事件满足 (1 le x le n,1 le y le m)
解析
部分分
我们可以对每一行的前m-1列开一个vector,同时给最后一列也开一个vector,模拟出队和入队的过程。显然在时间和空间上都不能通过。因此,我们来考虑一下优化。
空间优化
如果要输出出队者的编号,就意味着vector中需要保存所有的点。但是,对于每一行的前m-1个同学,他们的编号是可以直接计算得到的,不需要保存。那么每次判断一下出队的同学是不是前m-1个,是就直接计算,不是再到vector里面去找。
时间优化
耗时最久的部分在于每次删除时还要向左、向前看齐,意味着每次都要遍历最后一个vector。所以,考虑用权值线段树和vector一起维护每一行以及最后一列。权值线段树中保存的是当前哪些位置上有人,vector保存每次入队的历史记录。对于每次离队操作,用权值线段树查询这是第几个同学,然后到vector中查询编号。
按上述写法实现,会得到TLE&MLE的好成绩。
反向操作
即使使用权值线段树,修改每一个节点的复杂度还是过高。不妨反过来,初始默认每个位置都有人,就可以直接利用下标查询第k大。当有人出队时,就把那个人的位置置为1,查询第k大时减掉所有为1的点。这样就可以用一次修改操作来实现了。
动态开点
用线段树动态开点就可以优化空间复杂度。再加上之前提到过的空间优化,就可以通过本题。
细节
注意讨论在前m-1列和第m列的情况。修改前m-1列的信息时要将第m列中对应行的元素加入那一行的权值线段树中,同时更新第m列的值。
代码
#include <iostream>
#include <cstdio>
#include <vector>
#define int long long
#define N 300002
using namespace std;
struct SegmentTree{
int l,r,val;
}t[N*40];
int n,m,q,i,root[N],num;
vector<int> v[N];
int read()
{
char c=getchar();
int w=0;
while(c<'0'||c>'9') c=getchar();
while(c<='9'&&c>='0'){
w=w*10+c-'0';
c=getchar();
}
return w;
}
int kth(int &p,int l,int r,int x)
{
if(p==0) p=++num,t[p].val=0;
t[p].val++;
if(l==r) return l;
int mid=(l+r)/2;
int tmp=mid-l+1-t[t[p].l].val;
if(x<=tmp) return kth(t[p].l,l,mid,x);
return kth(t[p].r,mid+1,r,x-tmp);
}
signed main()
{
n=read();m=read();q=read();
int l1=m-1+q,l2=n+q;
for(i=1;i<=q;i++){
int x=read(),y=read();
if(y<m){
int pos1=kth(root[x],1,l1,y);
int ans=pos1<=m-1?m*(x-1)+pos1:v[x][pos1-m];
v[n+1].push_back(ans);
int pos2=kth(root[n+1],1,l2,x);
int id=pos2<=n?pos2*m:v[n+1][pos2-n-1];
v[x].push_back(id);
printf("%lld
",ans);
}
else{
int pos=kth(root[n+1],1,l2,x);
int ans=pos<=n?pos*m:v[n+1][pos-n-1];
v[n+1].push_back(ans);
printf("%lld
",ans);
}
}
return 0;
}