问题描述
有时候程序员有很奇怪的方法来隐藏他们的口令。Binny会选择一个字符串S(由N个小写字母组成,5<=N<=5,000,000),然后他把S顺时针绕成一个圈,每次取一个做开头字母并顺时针依次取字母而组成一个字符串。这样将得到一些字符串,他把它们排序后取出第一个字符串。把这个字符串的第一个字母在原字符串中的位置-1做为口令。
如字符串alabala,按操作的到7个字符串,排序后得:
aalabal
abalaal
alaalab
alabala
balaala
laalaba
labalaa
第一个字符串为aalabal,这个a在原字符串位置为7,7-1=6,则6为口令。
输入格式
第一行:一个数:N
第二行开始:字符串:S(每72个字符一个换行符)
输出格式
一行,为得到的口令
样例输入
7
anabana
样例输出
6
数据范围
题目满足:
30%的数据n<=10000
70%的数据n<=100000
100%的数据n<=5000000
解析
暴力的做法很好想。为了贪心,我们要保证每一位最小,就是每次用一个位置与当前最优的位置进行比较,如果相同就不断比较之后的字符,否则就可以更新最优解或继续往下枚举。
但这样显然会超时。仔细分析过程可以发现,我们可以如下来设计:
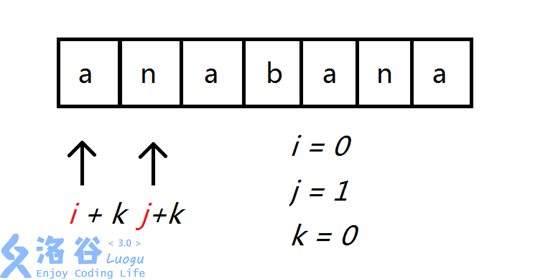
对于这个字符串,我们定义两个指针分别为 i 和 j 分别指向 ‘a’ 和 ’n’ 即 i = 0 j = 1 再定义一个累加器 k 则表示分别以 i 和 j 为首的字符串的第 k 个字符.根据贪心思想,每一项显然要选最小的最好。在这里 ’n’ 的字典序大于 ’a’ 那么j显然不会是我们所要的答案那么我们就对j进行移位即 j++接下来我们便重复上面的操作
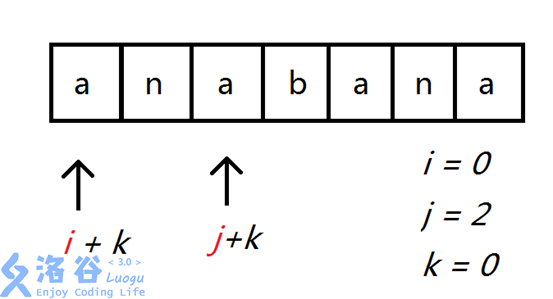
因为 i 和 j 所指的值是相同的,所以我们并不能通过比较这一位从而得出这两个字符串的顺序关系所以我们就要对 k 进行移位即 k++。我们对 i+k 和 j+k 所指的字符进行比较,显然可以得出 ’b’ 是比 ’n’ 要更优的那么这时候我们就要对i进行移位,因为在 [i ,i+k) 内我们都已经判断完了,那么我们就可以将 i 移到 i+k+1 继续接下来的判断。
但是我们还要考虑以下几个问题
- 当i=j时,我们的操作便无法正常的运行,因为显然的在i=j时,i+k=j+k,这样的话我们的k就会不断的增加从而导致WA
- i+k 和 j+k是可能越界的
- k是可能大于length的
解决方法如下:
- 当i=j时,j++
- 只要将i+k和j+k Mod length即可
- 限制k < length ,在k = length 直接返回i和j中位置较前的即可
代码
#include <iostream>
#include <cstdio>
#define N 5000002
using namespace std;
int n,i,j=1,k;
char c[N];
int main()
{
cin>>n;
for(i=0;i<n;i++) cin>>c[i];
i=0;
while(i<n&&j<n){
k=0;
while(c[(i+k)%n]==c[(j+k)%n]&&k<n) k++;
if(k==n) break;
if(c[(i+k)%n]>c[(j+k)%n]) i=i+k+1;
else j=j+k+1;
if(i==j) j++;
}
cout<<min(i,j)<<endl;
return 0;
}