Description
FGD 想从成都去上海旅游。在旅途中他希望经过一些城市并在那里欣赏风景,品尝风味小吃或者做其他的有趣的事情。经过这些城市的顺序不是完全随意的,比如说 FGD 不希望在刚吃过一顿大餐之后立刻去下一个城市登山,而是希望去另外什么地方喝下午茶。幸运的是,FGD 的旅程不是既定的,他可以在某些旅行方案之间进行选择。由于 FGD 非常讨厌乘车的颠簸,他希望在满足他的要求的情况下,旅行的距离尽量短,这样他就有足够的精力来欣赏风景。整个城市交通网络包含 N 个城市以及城市与城市之间的双向道路 M 条。城市自 1 至 N 依次编号,道路亦然。没有从某个城市直接到它自己的道路,两个城市之间最多只有一条道路直接相连,但可以有多条连接两个城市的路径。任意两条道路如果相遇,则相遇点也必然是这 N 个城市之一,在中途,由于修建了立交桥和下穿隧道,道路是不会相交的。每条道路都有一个固定长度。在中途,FGD 想要经过 K(K<=N-2)个城市。成都编号为 1,上海编号为 N,而 FGD 想要经过的 N 个城市编号依次为 2,3,...,K+1。举例来说,假设交通网络如下图。FGD 想要经过城市 2,3,4,5,并且在 2 停留的时候在 3 之前,而在 4,5 停留的时候在 3 之后。那么最短的旅行方案是1-2-4-3-4-5-8 , 总长度为 19。注意 FGD 为了从城市 2 到城市 4 可以路过城市 3,但不在城市 3 停留。这样就不违反 FGD 的要求了。并且由于 FGD 想要走最短的路径,因此这个方案正是 FGD需要的。
Input
第一行包含 3 个整数 N(2<=N<=20000),M(1<=M<=200000),K(0<=K<=20),意义如上所述。以下 M 行,每行包含 3 个整数 X,Y,Z,(1<=X<y<=n, 1<="Z=1000)表示城市 X与 Y 之间有一条双向道路。你可以认为输入文件使得一定能自成都到上海以及任何 FGD 想要去的城市。"下一行包含一个整数 G(0<=G<=K*(K-1)/2)。以下 G 行,每行包含 2 个整数 X Y,(2<=X,Y<=K+1)表示 FGD 想要在游览城市Y 之前,一定要游览城市 X。你可以认为至少存在一种满足所有限制的游览方案。
Output
只包含一行,包含一个整数,表示最短的旅行距离。
Sample Input
8 15 4
1 2 3
1 3 4
1 4 4
1 6 2
1 7 3
2 3 6
2 4 2
2 5 2
3 4 3
3 6 3
3 8 6
4 5 2
4 8 6
5 7 4
5 8 6
3
2 3
3 4
3 5
Sample Output
19
Hint
下面对应于题目中给出的例子。
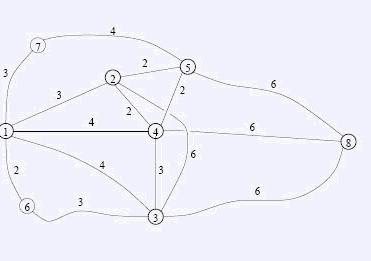
Solution
看到k非常小,就可以想到状态压缩的动态规划(先例:售货员的难题)。设f[i][j]表示经过的1到k+1的点的集合为i,当前所在点为j时的最短路径。那么有如下状态转移方程:
其中dis[j][l]表示从j到l的最短路径,那么为了判断一个点是否满足其先要访问的点的条件,可以用g[i]表示一个点i的所有前驱节点集合(同样用状态压缩),如果在状态转移方程中满足i&g[i]=g[i],就说明可行 。dis数组可以用SPFA跑出来。动态规划完成后,由于没有将第n个点计算在内,所以最终的答案为:
另外,为了表示方便和节省空间,第i个点在二进制集合中的位置可设为i-2,这样就可以从第0位开始表示了。
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
#define N 20002
#define M 200002
#define int long long
using namespace std;
int head[N],ver[M*2],nxt[M*2],edge[M*2],l;
int n,m,k,c,i,j,d[22][22],dis[N],f[1048576][22],g[22];
bool in[N];
int read()
{
char c=getchar();
int w=0;
while(c<'0'||c>'9') c=getchar();
while(c<='9'&&c>='0'){
w=w*10+c-'0';
c=getchar();
}
return w;
}
void insert(int x,int y,int z)
{
l++;
ver[l]=y;
edge[l]=z;
nxt[l]=head[x];
head[x]=l;
}
void SPFA(int s)
{
queue<int> q;
memset(in,0,sizeof(in));
memset(dis,0x3f,sizeof(dis));
q.push(s);
in[s]=1;
dis[s]=0;
while(!q.empty()){
int x=q.front();
q.pop();
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(dis[y]>dis[x]+edge[i]){
dis[y]=dis[x]+edge[i];
if(!in[y]){
q.push(y);
in[y]=1;
}
}
}
in[x]=0;
}
for(int i=1;i<=k+1;i++) d[s][i]=dis[i];
d[s][k+2]=dis[n];
}
signed main()
{
freopen("atr.in","r",stdin);
freopen("atr.out","w",stdout);
n=read();m=read();k=read();
for(i=1;i<=m;i++){
int u,v,w;
u=read();v=read();w=read();
insert(u,v,w);
insert(v,u,w);
}
c=read();
for(i=1;i<=c;i++){
int x,y;
x=read();y=read();
g[y]|=(1<<(x-2));
}
for(i=1;i<=k+1;i++) SPFA(i);
memset(f,-1,sizeof(f));
f[0][1]=0;
for(i=0;i<=(1<<k)-1;i++){
for(j=1;j<=k+1;j++){
if(f[i][j]!=-1){
for(l=2;l<=k+1;l++){
if((i&g[l])==g[l]){
if(f[i|(1<<(l-2))][l]==-1) f[i|(1<<(l-2))][l]=f[i][j]+d[j][l];
else f[i|(1<<(l-2))][l]=min(f[i|(1<<(l-2))][l],f[i][j]+d[j][l]);
}
}
}
}
}
int ans=1<<30;
for(i=1;i<=k+1;i++){
if(f[(1<<k)-1][i]!=-1) ans=min(ans,f[(1<<k)-1][i]+d[i][k+2]);
}
cout<<ans<<endl;
fclose(stdin);
fclose(stdout);
return 0;
}