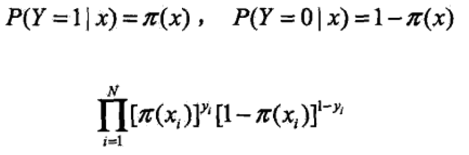模式识别课程-总结

1. Introduction

1.1 大纲

1. 贝叶斯
2. SVM
3. Unsupervised Learning & Clustering
4. Algorithm-independent ML
5. Application & Examples

1.2 PR ?

• 定义：输入原数据，提取它潜在的模式，并对模式做分类
• 目标：(1)对原数据去噪声；(2)建立若干model来近似描述数据背后对应的的真实概率分布；(3)选择一个能最佳近似的model, 并且基于最佳model 对数据中存在的若干模式进行分类

1.3 ML ?

• 基于数据开发一类可以依靠数据进行自我进化的算法
• 自动化地执行模式识别和制定决策

1.4 PR vs. ML

• PR: 问题的范畴，ML: 工具(方法)的范畴

1.5 "学习"的定义

• 定义任务T，性能度量P和训练经验E，如果计算机程序，在T上，以P衡量的性能，随着经验E而自我完善，则称这个计算机程序从经验E中学习

  

1.6 Pattern ?

• 混沌的反义词，它是一个有名称标识的实体

1.7 Pattern Class ?

• 两类差异：类间差异(同一类)和类别差异(不同类)

  

• 不同类别的描述：数学形式化(比如, 概率密度分布, i.e. probability density like Gaussian)

  

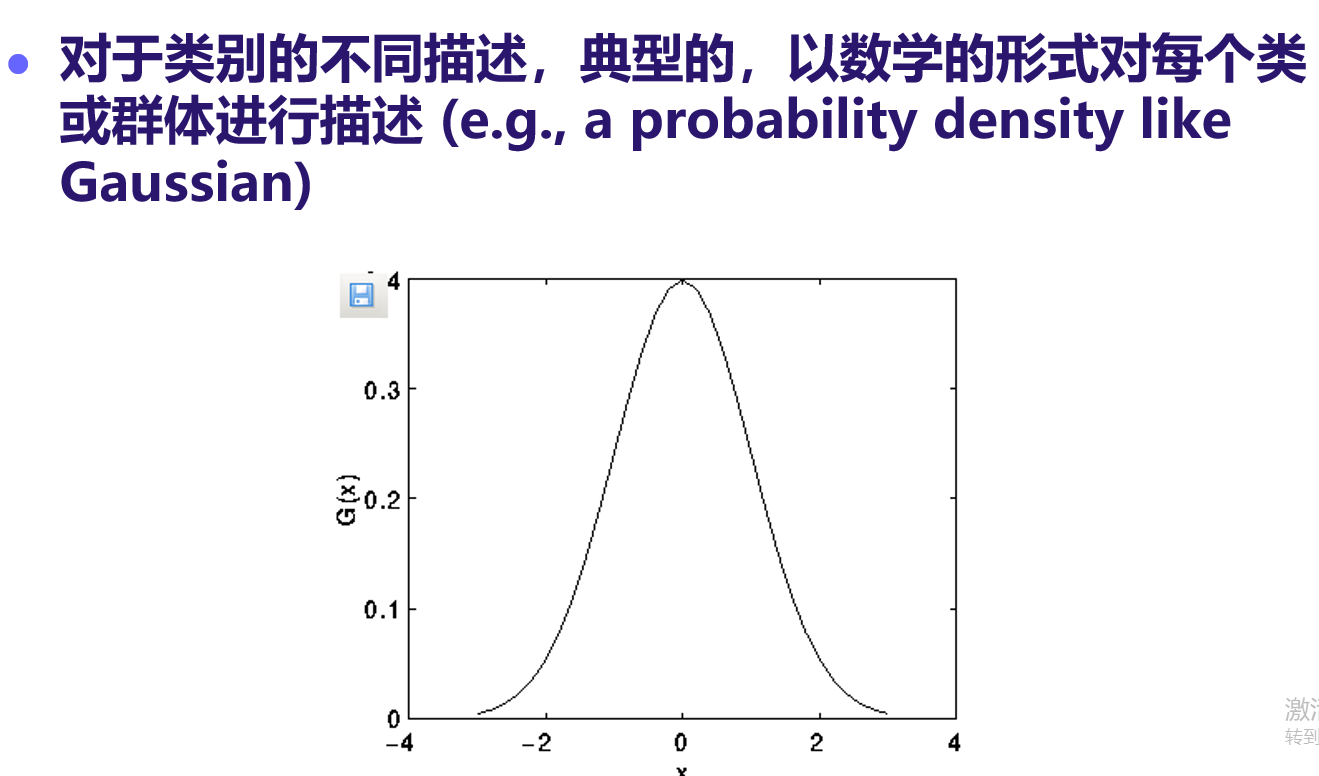
• 分类中的两类错误：

  • FP: 错误地把原本是负类的样本判定为正类
  • FN: 错误地把原本是正类的样本判定为负类

• 防止模型过拟合与提高模型的泛化性

1.8 设计 PR system

1. 流程

   

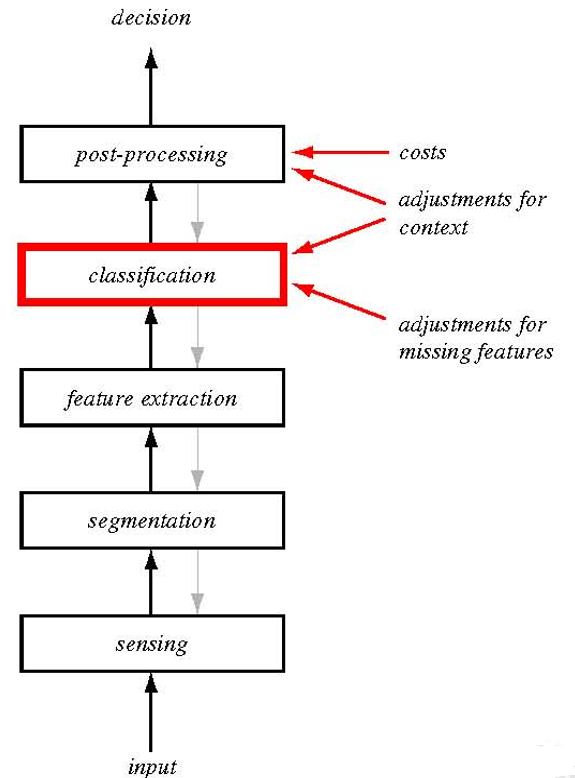
2. Design Cycle

   

3. 注意事项

   1. 噪声

   2. 特征提取

      

      

      

4. 模式的表达 (Pattern Representation)

   

5. 模型选择问题

   

6. 模型过拟合问题

   

7. 模型的泛化性

   

8. 计算复杂度

   

2. 贝叶斯

2.1 背景知识

1. 先验与后验概率：P(x) and P(y|x)， 【注意：p(x|y)是类条件概率】

2. 条件概率，全概率公式(略)

3. 贝叶斯公式：条件概率的变形

4. 分别基于先验p(yi)和后验概率p(yi|x) = bayes... 决策

   这里提到一个概念：似然likelihood到底是什么？见这张图：(似然的含义是：在已知x属于类别wi的条件下，x发生的概率)

   

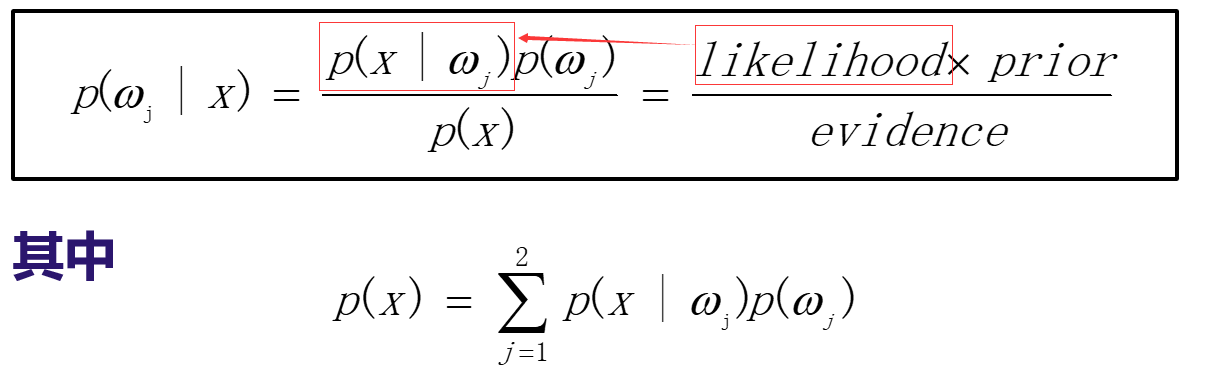
   • 后验概率具体是啥？举个例子，

     

5. 一个例题：利用贝叶斯公式，求 P(Ci|x)

   • 确定先验P(Ci)，easy，分别统计每个类别Ci包含的x的数量
   • 确定likilihood P(x|Ci)，分别考虑不同类别Ci条件下，x的分布直方图
   • 确定evidence P(x)，借助上面求的分量，以及全概率公式

2.2 更一般化的贝叶斯

• 条件风险：某个决策选择Wi的风险的条件即p(Wi|x)

  • 

  • 

  • 

    • 注：此处的w & a 的物理含义: w是真实标签，w0表示真实label为第0-th 类，w1即 1-th 类；而a表示 PR system的输出结果即所谓的决策行为，a0表示预测类别是第0-th 类，a1即预测结果为第 1-th 类

  • 所以依据min R 制定决策：

  • 一种特殊的情况，

    • 

• 由贝叶斯准则引出的具体的决策准则：

  • 假设P(x|Ci)这个likelihood服从多元混合高斯分布 (多元强调x是一个高维vector，混合强调的是多个高斯分布然后通过线性加权的方式组合起来) 的假设下，做各种case下(关于多元高斯的两个参数做各种假设) 的判别函数与决策边界的推导，下面记录几个我认为的重难点

• Case 1:

  • 

    • 核心是：假设每个高斯的sigma 相同且为常数

  • 

    • 这个gi(x)前面就已经充分讨论过，P(x|wi)的自变量还是x，wi不参与概率密度的公式

  • 

  • 

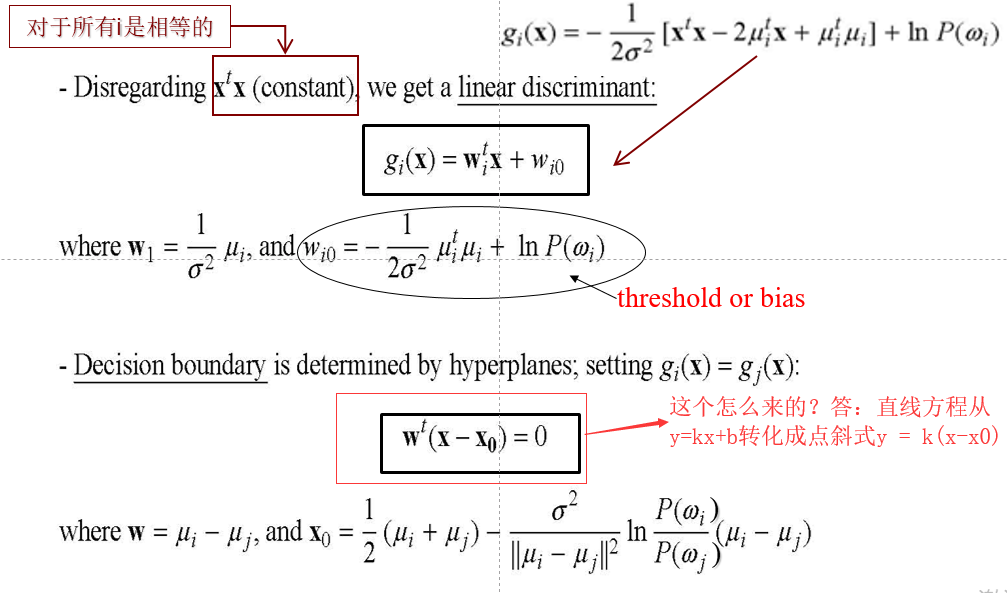
  • 有问题，如下：

    • 
    • 回答：
      • q1 显然
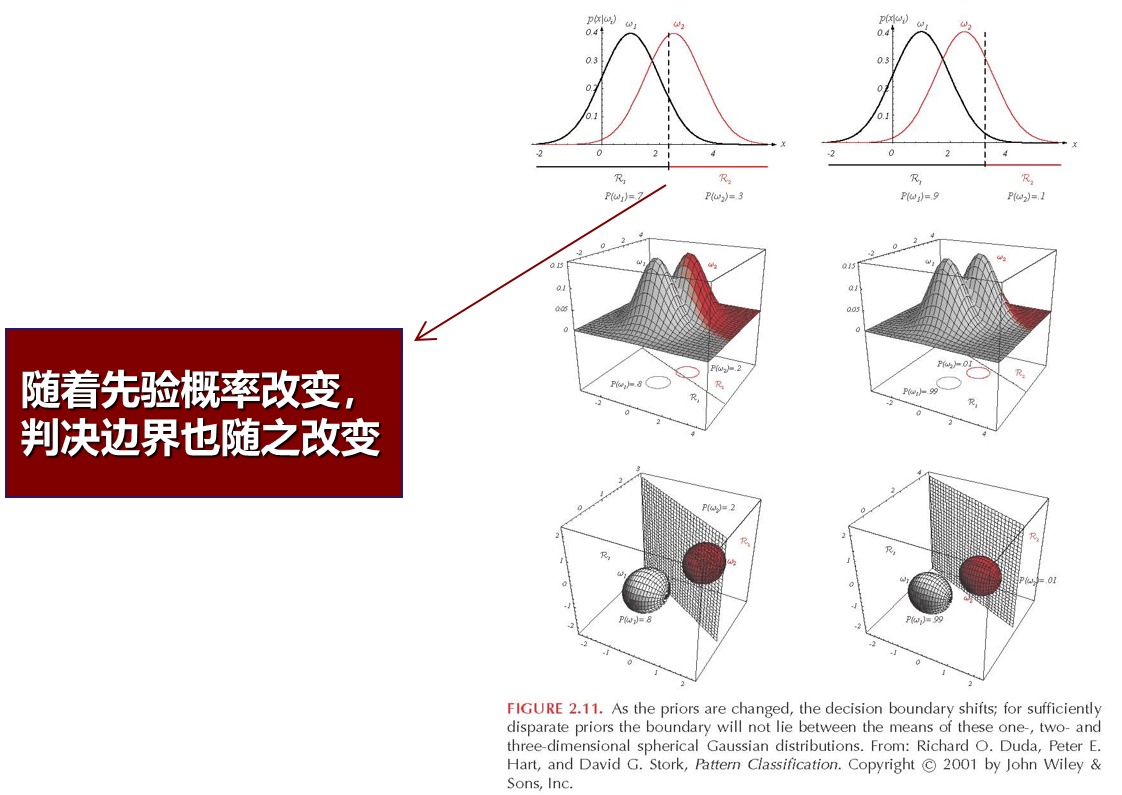
      • q2 描述的是：我的分界面(线)与 两个高斯分布即P(W0|x)与P(W1|x)的均值点的连线(因为高斯是一个球形分布，球心就是均值点)垂直，可以画图示意
      • q3 描述的是：点恰好落在分界面上
      • q4 描述的是：x0处于分界面上，x0更偏向于“体积更小”的那个高斯 （待验证）
      • q5 我的猜测是：因为delta很小，取平方后会更小(比如,0.0001)，作为乘积因子，导致第二项很小，就减低了 P(Wi)的作用

  • 

• Case 2:

  • 

  • 若干问题，

    

  • 突然对高斯分布的参数对于形状的影响，有个物理上的理解：均值决定这个高斯分布的中心的location，而方差决定这个高斯分布的形状是【高瘦还是矮胖，是圆形还是椭圆】

  • 

  • 

• Case 3:

  

• 有点复杂，暂时不讨论了

2.3 贝叶斯置信网

1. 作用：描述事件之间的概率依赖，最终求联合分布，也可以求其他单个事件的概率

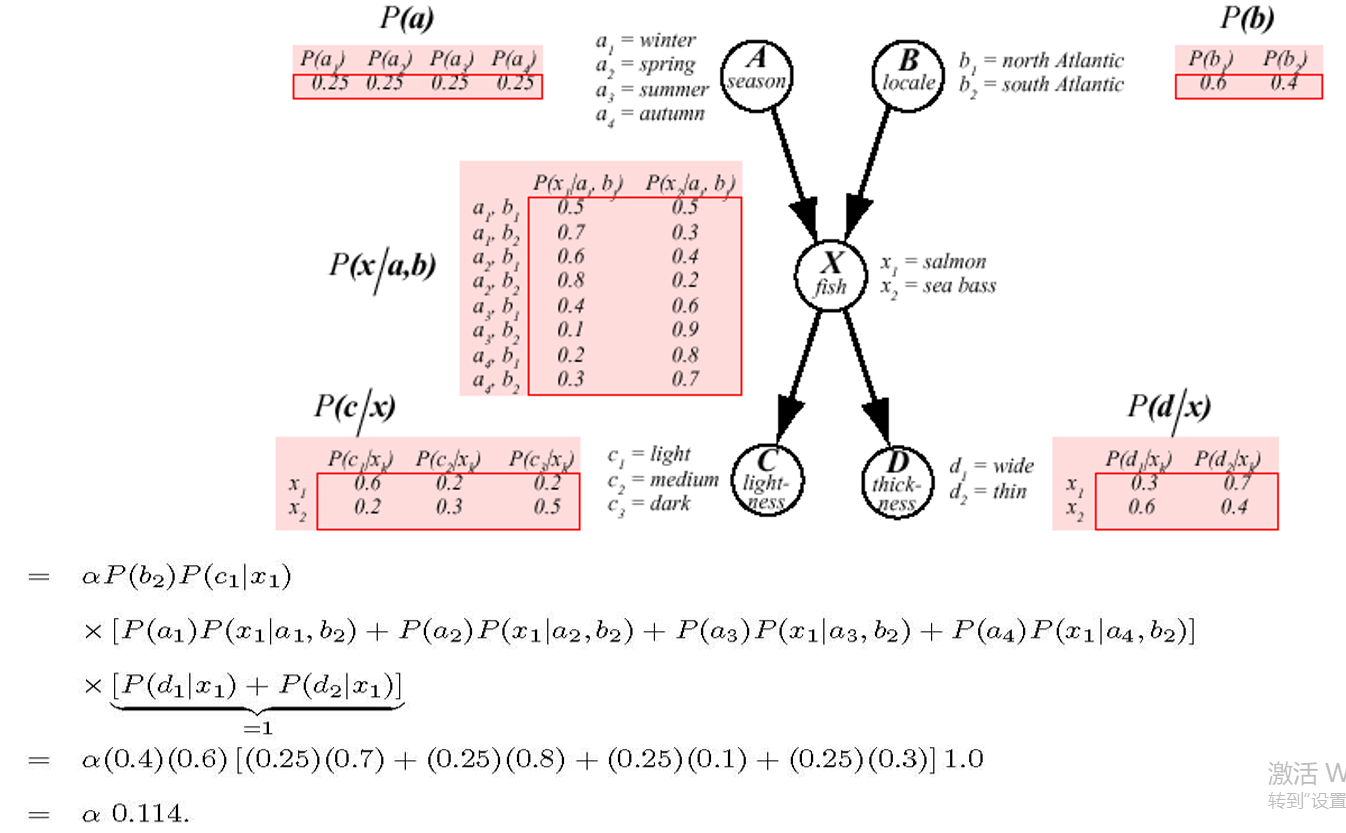
   • example-1

     

   • example-2

     

2. Bayesian Inference

   • 
   • 
   • 

3. Naive Bayes

   • 

   • 

   • 

   • 

   • 

   • 一些issue

     • 不符合独立性假设的，需要其他模型

     • 如果出现属性缺失，需处理

     • 分子为0，需要加入 平滑项(一个额外的参数)

     • 如果X的属性非离散，则：

       

4. Conclusion

   

3. Logistric Regression & CRF

3.1 LR (本质是classification)

1. 简单理解：

   • 二分类

   

   • 多分类

     

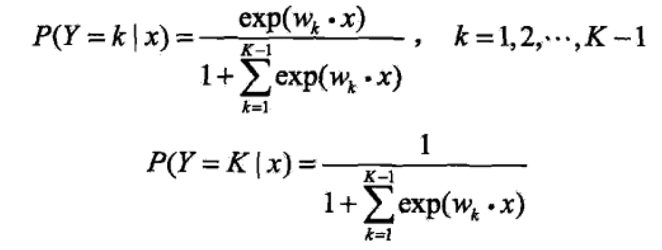
2. 训练(参数估计-极大似然估计)

   • 
   • 

3.2 CRF

1. 几个问题：

   • Markov property：属性之间彼此独立

   • MM(马尔科夫模型)与HMM(隐含马尔科夫模型)的区别：后者考虑了观测状态是由隐状态决定的

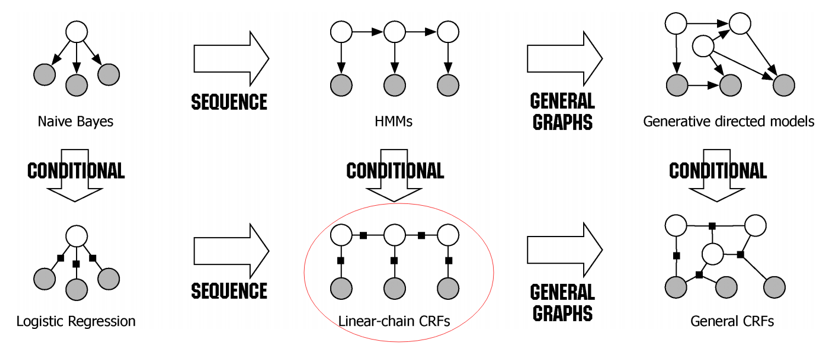
   • CRF与HMM的区别：将HMM中的马尔科夫性(属性之间彼此独立)升级为N-阶条件概率依赖

2. 直观理解CRF

   • 
   • 
   • 

3. 数学化

   • 
   • 

4. 训练(参数估计-最大似然估计)

   • 

5. 测试inference

   • 

   • CRF还没完全搞懂，有空再TODO

4. SVM

4.1 LLSVM

1. 本质：
   • 最大间隔的线性分类器
   • 只有 support vectors 是对模型有作用的(其他点没有贡献)，小样本统计学习
2. 数学形式化
   • 
   • 
   • 
   • 
   • 
   • 
   • 
   • 
3. Kernel Trick
   • 
   • 
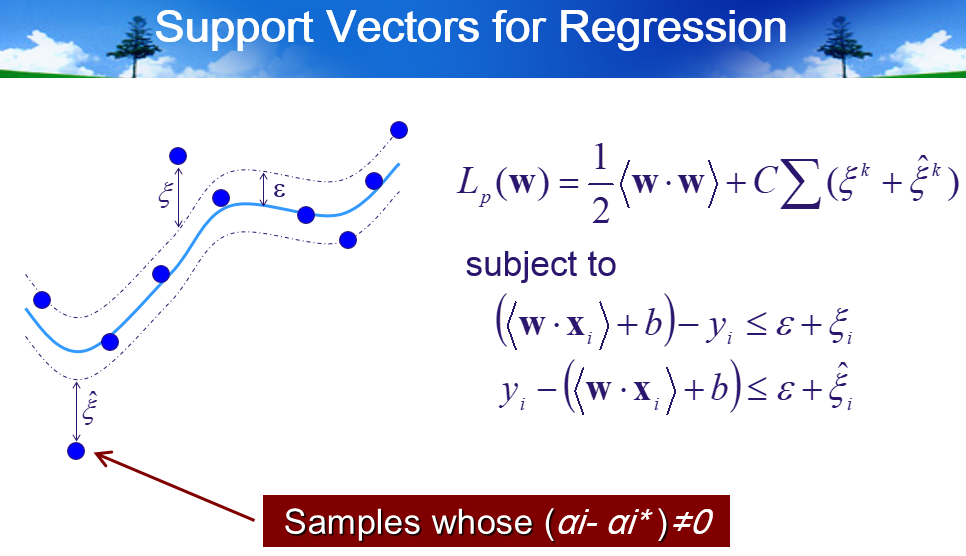
4. Introduce to SVR
   • 
5. Some important ingredients of SVMs
   • Support Vectors
     • 
     • 
   • Loss function
     • 
   • The selection of Hyperparameters
     • 

5. Clustering

5.1 Unsupervised Learning & Cluster Analysis

5.2 k-means & Fuzzy k-means

1. k-means:

   • 本质是一个交替优化的过程，初始化c个质心(mu1, mu2, ... muc)，循环进行交替优化直至停止条件：(1)根据质心重新扫描距离它最近的点并加入它所属的类别，(2)根据更新后类的所有点，计算新的质心

   • 细节：

     • 初始化质心：具体选几个质心？如何选择每一个？
     • 计算新的质心：计算当前类所有点的均值
     • 距离度量：欧式距离，余弦距离，相似度(泛化的定义)
     • 停止条件：质心不再发生大的变化或者迭代次数

   • 算法复杂度：o(T * c * n * d)，迭代次数 * num_class * num_point * num_feature

   • 一个难题：如何初始化质心(选几个？怎么选？)

     

   • 聚类效果的评价指标

     

   • 二分k-means

     • 参考博客

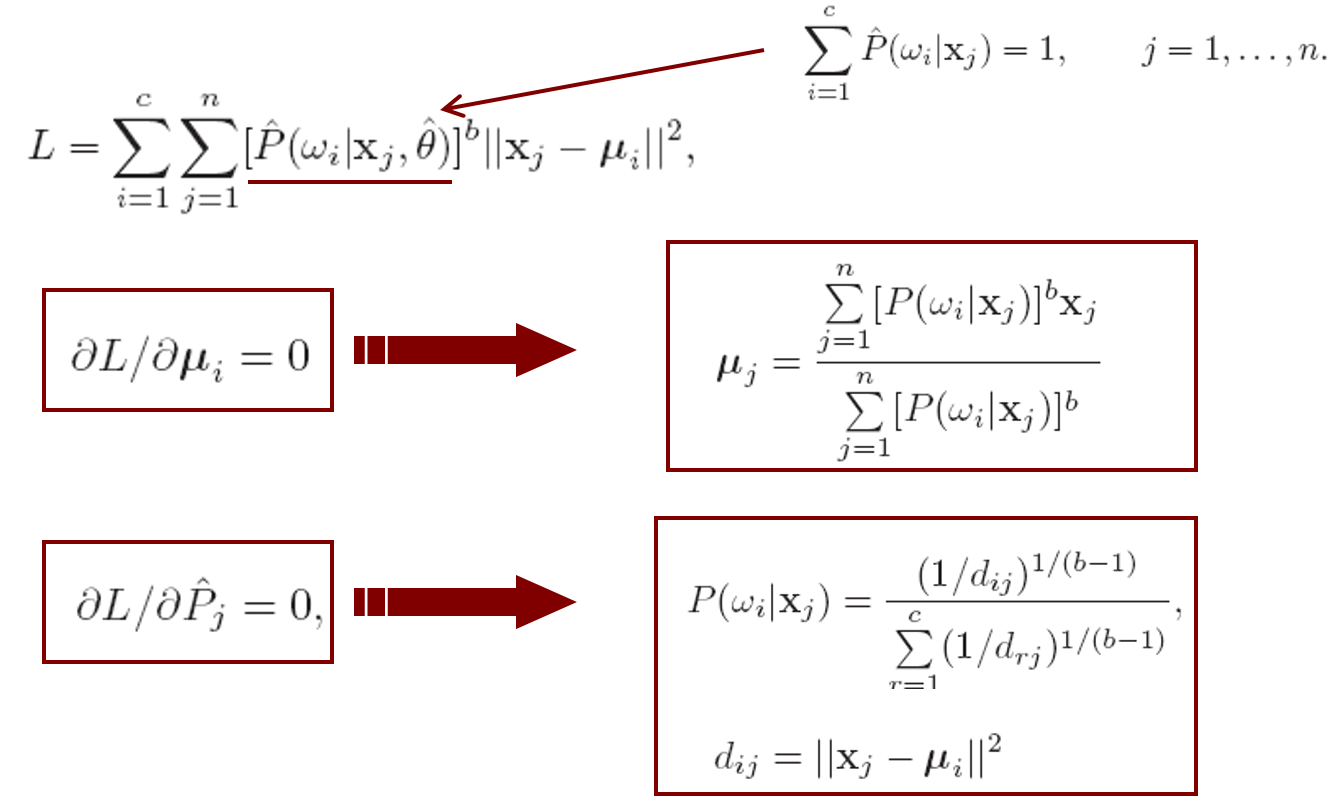
2. Fuzzy k-means

   • 
   • 
   • 

5.3 Theory

1. Mixture Densities and Identifiability
   • 
     • 上图的内涵是：(1)任意一个混合密度都能分解为：多个分量密度的线性加权求和，权重是P(Wj)，分量密度是p(x|Wj)，模型参数是theta
     • 如何做分类呢？一旦求解出了模型参数theta，首先将p(x)分解为c个p(x|Wj)，然后再利用贝叶斯设计最大后验分类器(MAP)
     • 
     • 
     • 
     • 
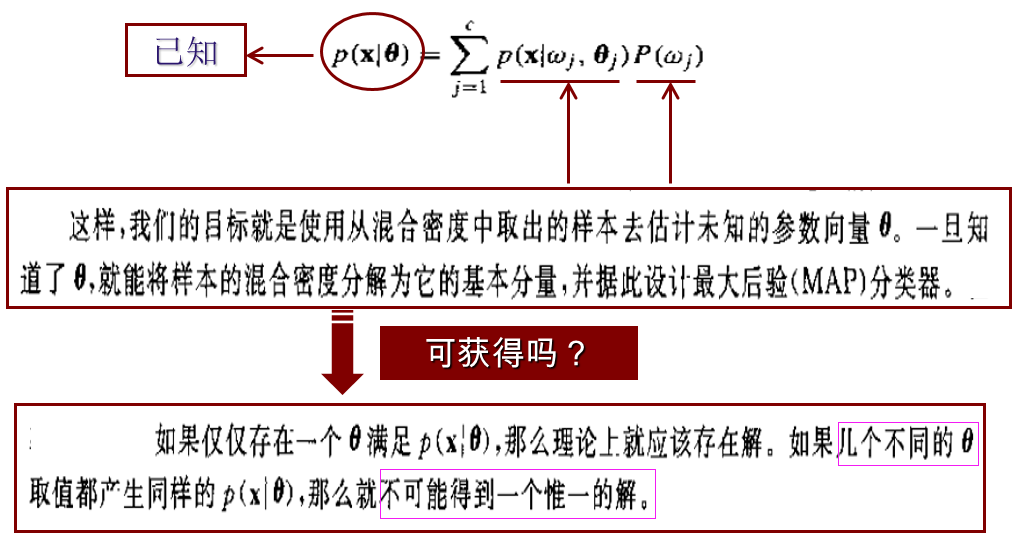
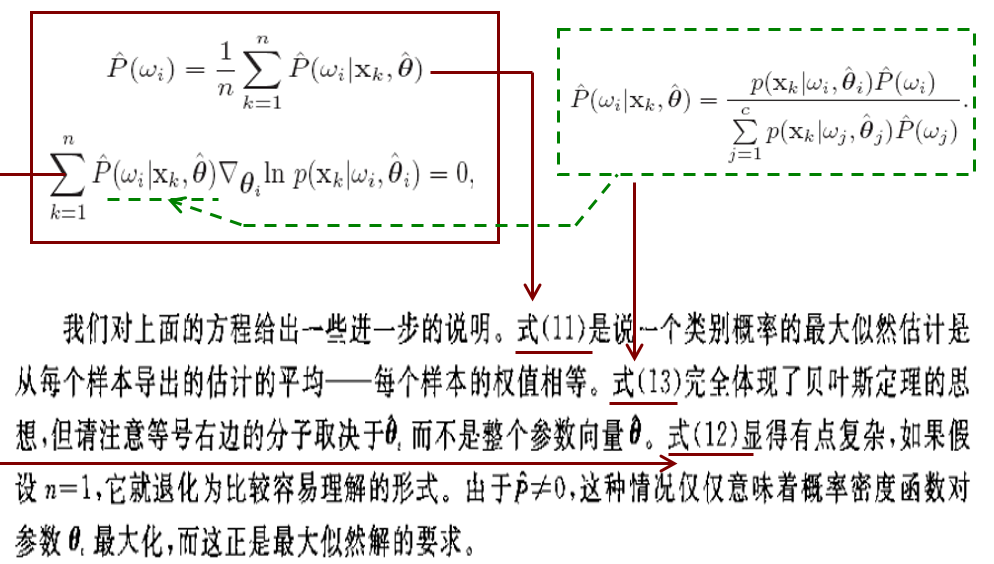
2. Maximum Likelihood Estimates
   • 
   • 
   • 
   • 
   • 
   • 
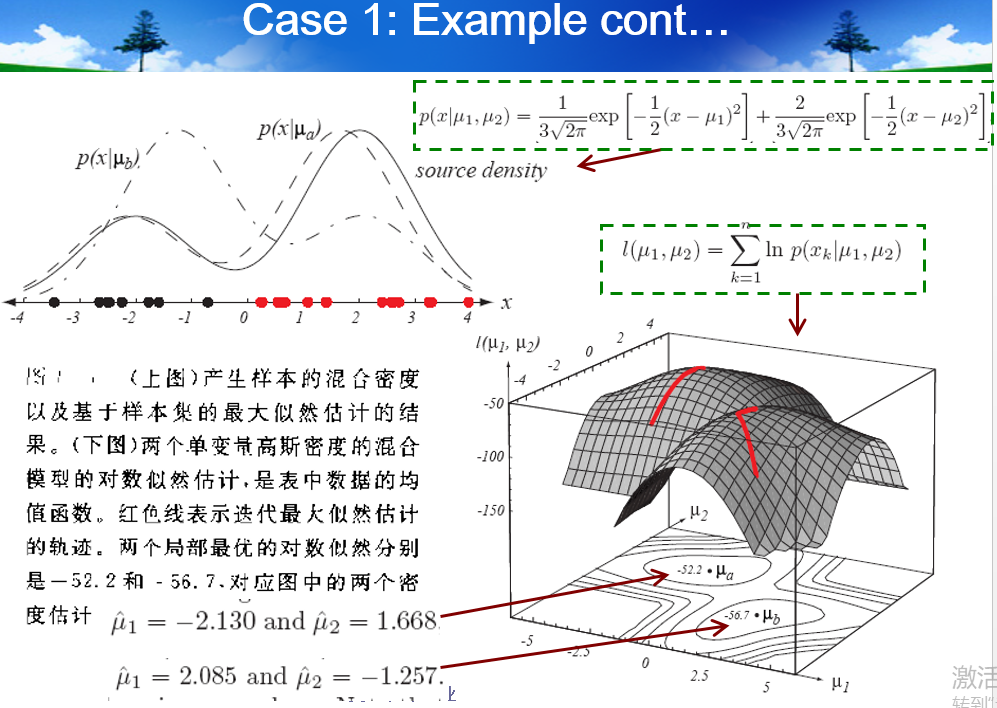
3. Application to Normal Mixtures
   • 
   • 
   • 
   • 
   • 
   • 

5.4 Data description and Clustering

1. Data description

   • 
   • 

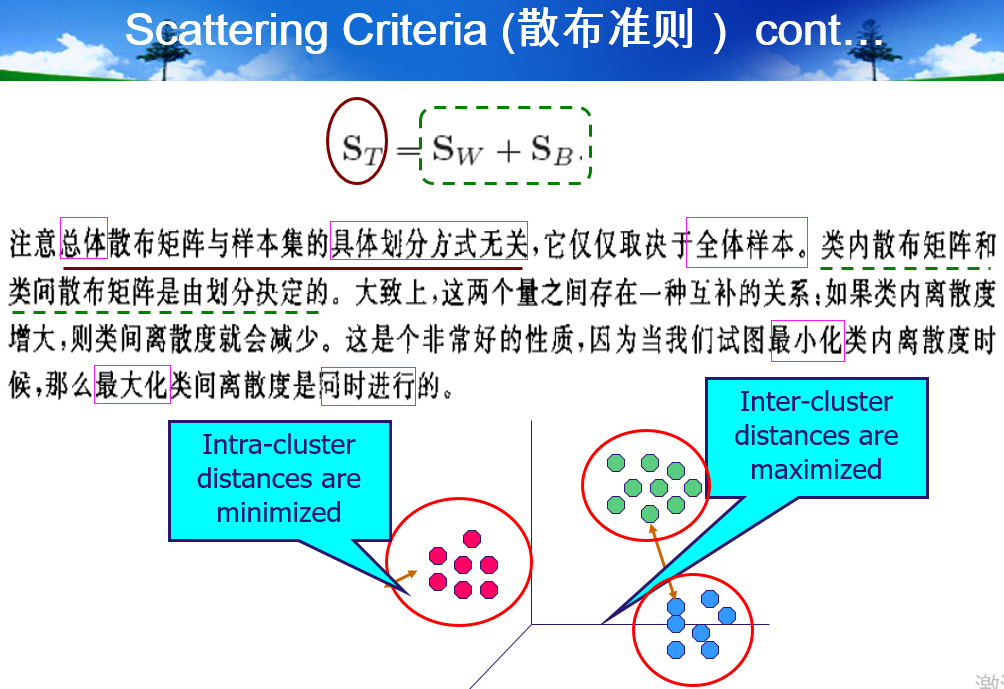
2. Clustering

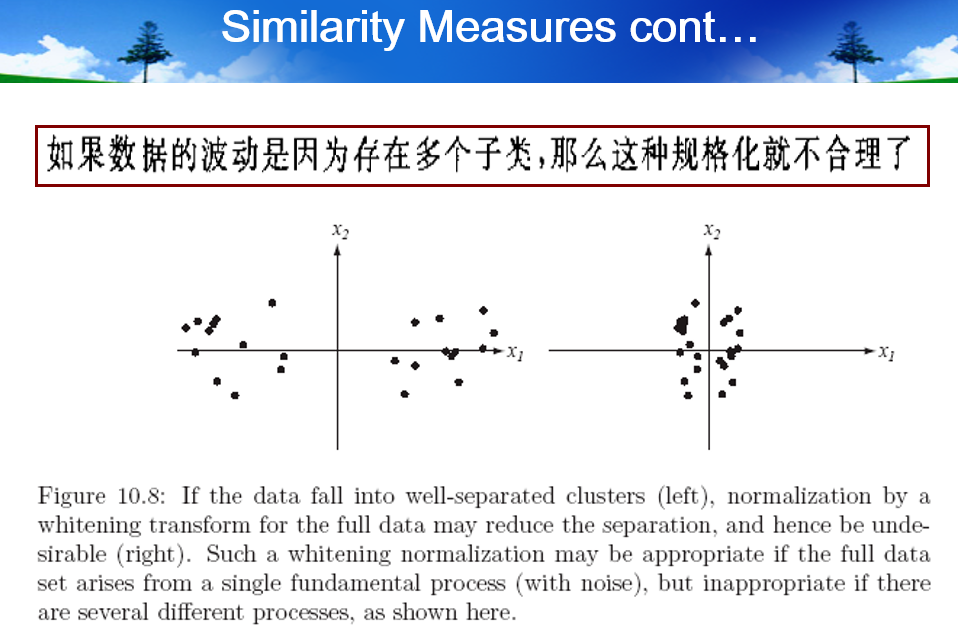
   • Similarity measure

     • 
     • 
     • 
     • 

   • Criterion function

     • 参考：http://ccftp.scu.edu.cn:8090/Download/4f294876-4c9b-4a3b-af5c-86ad5641948c.pdf
     • 
     • 
     • 
     • 

   • Iterative Optimization

     • 

     • 本质是和k-means的交替优化相同，反复循环下面两个：(1)得到一个划分，(2)重新更新所有点所属的划分，监督信号是：更新后的划分要使准则函数值performance更好

       

       • 这种爬山算法通用的问题是：如何选取初始点，一个简单的策略，随机选取多个初始点并各自运算，最终综合所有的结果(比如求均值)

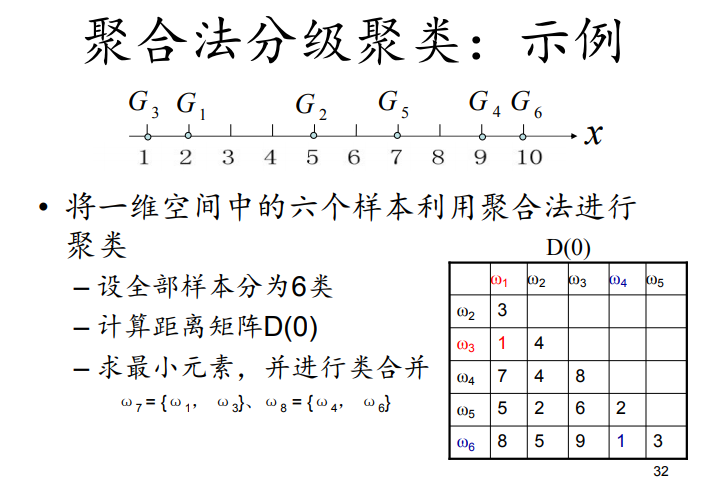
3. Hierarchical clustering

   • Difinition
     • 
   • Algorithm
     • 
     • 
     • 

4. Semi-supervised ( classification + clustering )

6. Algorithm-independent ML

6.1 与算法无关的具体内涵

1. 数学基础不依赖于所采用的特定分类器和特定学习算法
2. 可以与不同的学习算法组合使用

6.2 NFL & Ugly Ducking Thorem & Occam razor

1. NFL(No Free Lunch): (1) 学习算法必须要做与问题领域相关的假设才能由于其他算法，完全无任何假设条件下，所有算法的效果是相同的; (2)不存在万能算法，任何算法都只能在它能很好匹配的问题领域优于其他算法
2. Ducking Thorem: 不存在与问题无关的“最好的”特征或者属性，再次比较一定要基于具体问题
3. Occam razor: 除非有必要，否则越简单越好

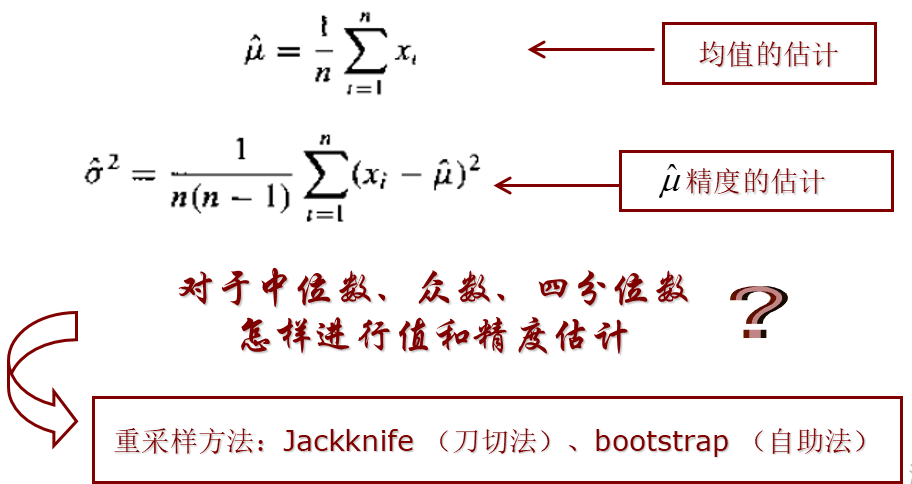
6.3 Resampling for estimating statistics

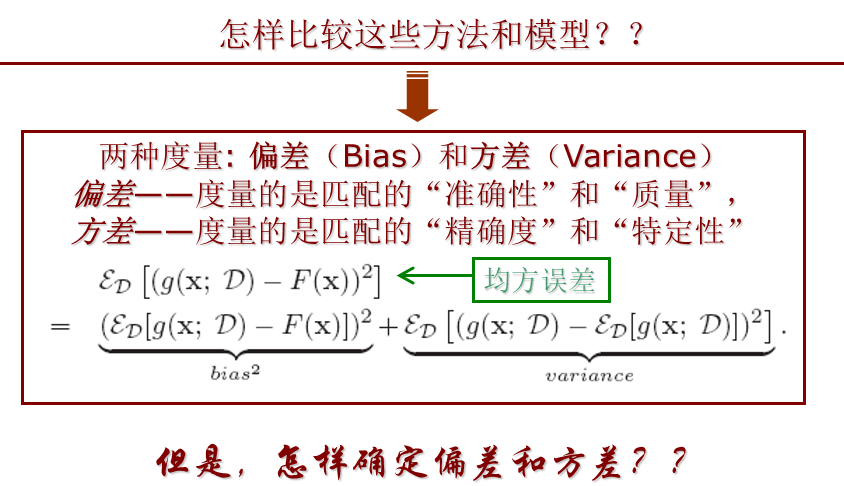
1. Bias and Variance
   • 
   • 
2. Jackknife
   • 
3. Bootstrap
   • 
   • 

6.4 Resampling for classifier design

1. Bagging
   • 
   • Bagging = Bootstrap + aggregation
   • 
2. Boosting
   • 
   • Boosting的核心理念是：(1)串行依次堆叠多个分类器，(2)下一个分类器将重点放在上一个分类器分错的样本点上，期待纠正上一个分类器犯的错误
   • 
   • 
3. AdaBoost
   • 
   • 
   • 
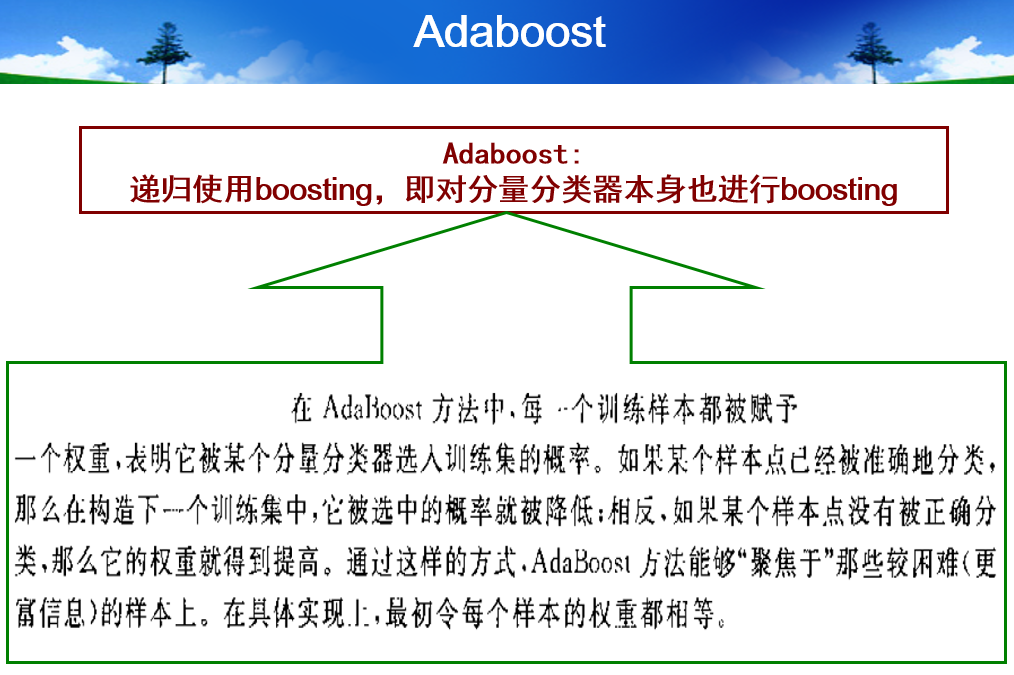
     • 注意：我个人的疑惑和反思：从Adaboost的思路来讲，必须要确保 E_k < 1/2，不然下面的权重更新公式就出现逻辑矛盾(正确分类的点的权重乘了一个大于1的放大因子，错误分类的点的权重反而乘了一个小于1的缩小因子)

6.5 Estimating and comparing classifiers

1. Cross validation
   • k-fold即要数据集D分成k组，每次留一组作为validation set，其他组作为training set，所以形成k个子数据集
2. Jackknife and Bootstrap Estimation of Classification
   • 即留一法，k==n(n是训练集D的样本数目)
   • 

6.6 Conclusion

•