A. Lunar New Year and Cross Counting
题解:

1 #include <cstdio> 2 3 using namespace std; 4 const int maxn=500+10; 5 const int dx[]={1,1,-1,-1}; 6 const int dy[]={1,-1,1,-1}; 7 char G[maxn][maxn]; 8 int n; 9 int ans; 10 int main(){ 11 scanf("%d",&n); 12 for(int i=0;i<n;i++) 13 scanf("%s",G[i]); 14 for(int i=0;i<n;i++){ 15 for(int j=0;j<n;j++){ 16 if(G[i][j]=='X'){ 17 int flag=1; 18 for(int k=0;k<4;k++){ 19 int nx=i+dx[k]; 20 int ny=j+dy[k]; 21 if(G[nx][ny]!='X'){ 22 flag=0; 23 break; 24 } 25 } 26 if(flag){ 27 ans++; 28 } 29 } 30 } 31 } 32 printf("%d ",ans); 33 return 0; 34 }
B. Lunar New Year and Food Ordering
题解:

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <queue> 6 7 using namespace std; 8 const int maxn=1e5+100; 9 int a[maxn],c[maxn]; 10 struct HeapNode{ 11 int idx,cost; 12 bool operator<(const HeapNode& rhs)const{ 13 return (cost>rhs.cost||(cost==rhs.cost&&idx>rhs.idx)); 14 } 15 }; 16 int n,m; 17 int main(){ 18 scanf("%d%d",&n,&m); 19 for(int i=1;i<=n;i++){ 20 scanf("%d",&a[i]); 21 } 22 for(int i=1;i<=n;i++){ 23 scanf("%d",&c[i]); 24 } 25 priority_queue<HeapNode>q; 26 for(int i=1;i<=n;i++){ 27 q.push((HeapNode){i,c[i]}); 28 } 29 for(int i=1;i<=m;i++){ 30 int t,d; 31 scanf("%d%d",&t,&d); 32 if(a[t]>=d){ 33 a[t]-=d; 34 //printf("!"); 35 printf("%I64d ",(long long)d*c[t]); 36 }else{ 37 long long res=(long long)a[t]*c[t]; 38 d-=a[t]; 39 a[t]=0; 40 while(!q.empty()&&d){ 41 HeapNode u=q.top();q.pop(); 42 // printf("@%d %d ",u.idx,a[u.idx]); 43 if(a[u.idx]>d){ 44 res+=(long long)d*u.cost; 45 a[u.idx]-=d; 46 q.push(u); 47 d=0; 48 break; 49 }else{ 50 res+=(long long)a[u.idx]*u.cost; 51 d-=a[u.idx]; 52 a[u.idx]=0; 53 } 54 } 55 if(d)printf("0 "); 56 else 57 printf("%I64d ",res); 58 } 59 } 60 return 0; 61 }
C. Lunar New Year and Number Division
题解:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <iostream> 5 6 using namespace std; 7 const int maxn=3e5+10; 8 int a[maxn]; 9 int n; 10 int main(){ 11 scanf("%d",&n); 12 for(int i=1;i<=n;i++){ 13 scanf("%d",&a[i]); 14 } 15 sort(a+1,a+1+n); 16 long long ans=0; 17 for(int i=1;i<=n/2;i++){ 18 ans+=(a[i]+a[n-i+1])*(a[i]+a[n-i+1]); 19 } 20 printf("%I64d ",ans); 21 return 0; 22 }
D. Lunar New Year and a Wander
题解:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <iostream> 5 #include <vector> 6 #include <queue> 7 8 using namespace std; 9 const int maxn=1e5+100; 10 int vis[maxn]; 11 int n,m,sz; 12 vector<int>G[maxn]; 13 void dfs(int u){ 14 vis[u]=1; 15 printf("%d ",u); 16 for(int i=0;i<G[u].size();i++){ 17 int v=G[u][i]; 18 if(!vis[v]){ 19 dfs(v); 20 } 21 } 22 } 23 int main(){ 24 scanf("%d%d",&n,&m); 25 for(int i=1;i<=m;i++){ 26 int a,b; 27 scanf("%d%d",&a,&b); 28 G[a].push_back(b); 29 G[b].push_back(a); 30 } 31 priority_queue<int,vector<int>,greater<int> >q; 32 q.push(1); 33 vis[1]=1; 34 while(!q.empty()){ 35 int u=q.top();q.pop(); 36 printf("%d ",u); 37 for(int i=0;i<G[u].size();i++){ 38 int v=G[u][i]; 39 if(!vis[v]){ 40 vis[v]=1; 41 q.push(v); 42 } 43 } 44 } 45 46 return 0; 47 }
E. Lunar New Year and Red Envelopes
题意:
时间线为从1到n,第i个红信封可以打开在时间[si,ti]之间,里面有wi个硬币。如果他打开了这个信封,那么他不能再打开其他的信封直到时间di,di>=ti>=si。 Bob会贪心的去打开这些信封,如果当前时间Bob可以打开好几个信封,那么他会选择硬币最多的那个打开,如果有多个信封应该都是最多,那么Bob会选择d值最大的那个。如果仍然有多个,Bob会随机选一个。
Alice不希望Bob获得太多的硬币,因此她可以骚扰Bob m次,如果Alice决定骚扰Bob在时间x,那么Bob在时间x不能做任何事情。请你计算Bob可以获得的最少的硬币数如果Alicee采取最优策略。
题解:
1.预处理出在时间i点,要选择哪个信封。
2.设dp[i][j]处理到前i个,已经使用了j次骚扰的最少值。那么(i,j)可以转移到(d[i]+1,j)和(i+1,j+1)

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <iostream> 5 #include <set> 6 #include <vector> 7 8 using namespace std; 9 typedef long long LL; 10 11 const LL INF=1e18; 12 const int maxn=1e5+10; 13 const int maxm=200+10; 14 int n,m,k; 15 struct Even{ 16 int d,w,t; 17 bool operator<(const Even& rhs)const{ 18 return w>rhs.w||(w==rhs.w&&d>rhs.d); 19 } 20 }even[maxn]; 21 vector<Even>st[maxn],en[maxn]; 22 LL f[maxn][maxm]; 23 24 int main(){ 25 scanf("%d%d%d",&n,&m,&k); 26 for(int i=1;i<=k;i++){ 27 int s,t,d,w; 28 scanf("%d%d%d%d",&s,&t,&d,&w); 29 st[s].push_back((Even){d,w,1}); 30 en[t+1].push_back((Even){d,w,-1}); 31 } 32 multiset<Even>S; 33 for(int i=1;i<=n;i++){ 34 for(int j=0;j<st[i].size();j++) 35 S.insert(st[i][j]); 36 for(int j=0;j<en[i].size();j++){ 37 multiset<Even>::iterator it=S.find(en[i][j]); 38 if(it!=S.end()) 39 S.erase(it); 40 } 41 if(S.empty()){ 42 even[i]=(Even){0,0,0}; 43 }else{ 44 even[i]=*S.begin(); 45 } 46 } 47 for(int i=1;i<=n+1;i++){ 48 for(int j=0;j<=m;j++){ 49 f[i][j]=INF; 50 } 51 } 52 // for(int i=1;i<=n;i++){ 53 // printf("%d %d %d ",i,even[i].d,even[i].w); 54 // } 55 f[1][0]=0; 56 for(int i=1;i<=n;i++){ 57 for(int j=0;j<=m;j++){ 58 if(f[i][j]>=INF) 59 continue; 60 if(even[i].w==0){ 61 f[i+1][j]=min(f[i+1][j],f[i][j]); 62 }else{ 63 f[even[i].d+1][j]=min(f[even[i].d+1][j],f[i][j]+even[i].w); 64 if(j!=m)f[i+1][j+1]=min(f[i+1][j+1],f[i][j]); 65 } 66 } 67 } 68 LL ans=INF; 69 for(int i=0;i<=m;i++) 70 ans=min(ans,f[n+1][i]); 71 printf("%I64d ",ans); 72 return 0; 73 }
E. Lunar New Year and Red Envelopes
题意:
给出三个整数k,m和n和一个递推式。当i<k的时候,f1,f2,...,fk-1=1。当i>k的时候递推式如下。
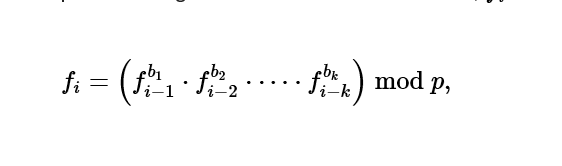
现在已知fn=m,求fk的值。
题解:
手推一下可以发现,fi一定可以表示为fk^x的形式。设f[i]=f[k]^x[i],我们可以推出x[i]=x[i-1]*b[1]+x[i-2]*b[2]+...+x[i-k]*b[k].而f[n]=f[k]^x[n]=m,x[n]可以由矩阵快速幂得到。然后998244353的原根为3,由原根的性质可以知道一定可以表示为3^c=m(mod p),那么c可以通过bsgs得到。然后3^c=f[k]^x[n]=3^(a*x[n])(mod p),然后由欧拉定理可以知道,a^c mod p=a^(c mod (p-1)) mod p。所以c =a*x[n]( mod p-1 ),这个公式显然可以用扩展欧几里得求解出a的值。所以f[k]=3^a mod p.

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <cmath> 5 #include <map> 6 7 using namespace std; 8 typedef long long LL; 9 const int maxn=100+10; 10 const int mod=998244353; 11 int k,n,m; 12 int b[maxn]; 13 LL q_pow(LL a,LL n,LL p){ 14 LL res=1; 15 while(n){ 16 if(n&1)res=res*a%p; 17 a=a*a%p; 18 n>>=1; 19 } 20 return res; 21 } 22 LL bsgs(LL a,LL b,LL p){ 23 map<long ,long>hash; 24 hash.clear(); 25 b%=p; 26 int t=(int)sqrt(p)+1; 27 for(int j=0;j<t;j++){ 28 int val=(long long)b*q_pow(a,j,p)%p; 29 hash[val]=j; 30 } 31 a=q_pow(a,t,p); 32 if(a==0){ 33 if(b==0){ 34 return 1; 35 }else{ 36 return -1; 37 } 38 } 39 for(int i=0;i<=t;i++){ 40 int val=q_pow(a,i,p); 41 int j=hash.find(val)==hash.end()?-1:hash[val]; 42 if(j>=0&&i*t-j>=0){ 43 return i*t-j; 44 } 45 } 46 return -1;//无解时返回-1 47 } 48 49 struct Matrix{ 50 int n,m; 51 LL a[maxn][maxn]; 52 void init(){ 53 memset(a,0,sizeof(a)); 54 for(int i=0;i<maxn;i++) 55 a[i][i]=1; 56 } 57 }; 58 Matrix mul(Matrix a,Matrix b){ 59 Matrix res; 60 res.n=a.n,res.m=b.m; 61 for(int i=0;i<a.n;i++){ 62 for(int j=0;j<b.m;j++){ 63 res.a[i][j]=0; 64 for(int k=0;k<a.m;k++){ 65 res.a[i][j]=(res.a[i][j]+a.a[i][k]*b.a[k][j])%(mod-1); 66 res.a[i][j]%(mod-1); 67 } 68 } 69 } 70 return res; 71 } 72 Matrix qpow(Matrix a,int n){ 73 Matrix res; 74 res.n=res.m=a.n; 75 res.init(); 76 while(n){ 77 if(n%2)res=mul(res,a); 78 a=mul(a,a); 79 n>>=1; 80 } 81 return res; 82 } 83 void gcd(LL a,LL b,LL& d,LL& x,LL& y){ 84 if(!b){ 85 d=a;x=1;y=0; 86 }else{ 87 gcd(b,a%b,d,y,x); 88 y-=x*(a/b); 89 } 90 } 91 92 int main(){ 93 scanf("%d",&k); 94 for(int i=0;i<k;i++){ 95 scanf("%d",&b[i]); 96 } 97 scanf("%d%d",&n,&m); 98 Matrix in; 99 in.n=in.m=k; 100 for(int i=0;i<k;i++){ 101 in.a[0][i]=b[i]; 102 } 103 for(int i=1;i<k;i++){ 104 for(int j=0;j<k;j++){ 105 if(j==i-1)in.a[i][j]=1; 106 else in.a[i][j]=0; 107 } 108 } 109 in=qpow(in,n-k); 110 111 Matrix st; 112 st.n=k,st.m=1; 113 for(int i=0;i<st.n;i++) 114 st.a[i][0]=(i==0?1:0); 115 in=mul(in,st); 116 // printf("!%I64d ",in.a[0][0]); 117 LL xn=in.a[0][0]; 118 //xn=729806697; 119 LL c=bsgs(3,m,mod); 120 //printf("!!%I64d ",c); 121 //printf("@I64d ",q_pow(3,c,mod)); 122 LL d,x,y; 123 gcd(xn,mod-1,d,x,y); 124 if(c%d){ 125 printf("-1 "); 126 return 0; 127 } 128 //printf("%I64d ",d); 129 130 x=(x+(mod-1)/d)%(mod-1); 131 x=x*(c/d); 132 //printf("!!!%I64d %I64d ",x,y); 133 LL ans=q_pow(3,x,mod); 134 printf("%I64d ",ans); 135 return 0; 136 }
