踪电子表格中的单元格（Spreadsheet Tracking, ACM/ICPC World Finals 1997, UVa512）

有一个r行c列（1≤r，c≤50）的电子表格，行从上到下编号为1～r，列从左到右编号为1 ～c。如图4-2（a）所示，如果先删除第1、5行，然后删除第3, 6, 7, 9列，结果如图4-2（b） 所示。

接下来在第2、3、5行前各插入一个空行，然后在第3列前插入一个空列，会得到如图4- 3所示结果。

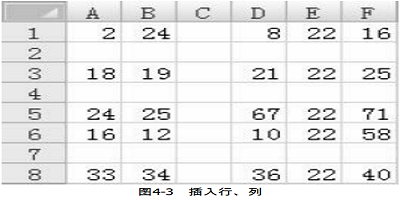
你的任务是模拟这样的n个操作。具体来说一共有5种操作：

　　EX r1 c1 r2 c2交换单元格(r1,c1),(r2,c2)。

　　<command>A x1 x2 … xA 插入或删除A行或列（DC-删除列，DR-删除行，IC-插入 列，IR-插入行，1≤A≤10）。

在插入／删除指令后，各个x值不同，且顺序任意。接下来是q个查询，每个查询格式 为“r c”，表示查询原始表格的单元格(r,c)。对于每个查询，输出操作执行完后该单元格的新 位置。输入保证在任意时刻行列数均不超过50。

【分析】

　　最直接的思路就是首先模拟操作，算出最后的电子表格，然后在每次查询时直接在电子 表格中找到所求的单元格。

（直接上代码，不是很难理解）

#include<stdio.h>
#include<string.h>
#define maxd 100
#define BIG 10000
int r, c, n, d[maxd][maxd], d2[maxd][maxd], ans[maxd][maxd], cols[maxd];
void copy(char type, int p, int q) {
    if(type == 'R') {
        for(int i = 1; i <= c; i++)
            d[p][i] = d2[q][i];
    } 
    else {
        for(int i = 1; i <= r; i++)
            d[i][p] = d2[i][q];
    }
}
void del(char type) {
    memcpy(d2, d, sizeof(d));
    int cnt = type == 'R' ? r : c, cnt2 = 0;
    for(int i = 1; i <= cnt; i++) {
        if(!cols[i]) copy(type, ++cnt2, i);
    }
    if(type == 'R') r = cnt2; else c = cnt2;
}
void ins(char type) {
    memcpy(d2, d, sizeof(d));
    int cnt = type == 'R' ? r : c, cnt2 = 0;
    for(int i = 1; i <= cnt; i++) {
        if(cols[i]) copy(type, ++cnt2, 0);
        copy(type, ++cnt2, i);
    }
    if(type == 'R') r = cnt2; else c = cnt2;
}
int main() {
    int r1, c1, r2, c2, q, kase = 0;
    char cmd[10];
    memset(d, 0, sizeof(d));
    while(scanf("%d%d%d", &r, &c, &n) == 3 && r) {
        int r0 = r, c0 = c;
        for(int i = 1; i <= r; i++)
            for(int j = 1; j <= c; j++)
                d[i][j] = i*BIG + j;
    while(n--) {
        scanf("%s", cmd);
        if(cmd[0] == 'E') {
            scanf("%d%d%d%d", &r1, &c1, &r2, &c2);
            int t = d[r1][c1]; d[r1][c1] = d[r2][c2]; d[r2][c2] = t;
        } 
        else {
            int a, x;
            scanf("%d", &a);
            memset(cols, 0, sizeof(cols));
            for(int i = 0; i < a; i++) { scanf("%d", &x); cols[x] = 1; }
            if(cmd[0] == 'D') del(cmd[1]); else ins(cmd[1]);
        }
    }
    memset(ans, 0, sizeof(ans));
    for(int i = 1; i <= r; i++)
        for(int j = 1; j <= c; j++) {
            ans[d[i][j]/BIG][d[i][j]%BIG] = i*BIG+j;
    }
    if(kase > 0) printf("
");
    printf("Spreadsheet #%d
", ++kase);
    scanf("%d", &q);
    while(q--) {
    scanf("%d%d", &r1, &c1);
    printf("Cell data in (%d,%d) ", r1, c1);
    if(ans[r1][c1] == 0) printf("GONE
");
    else printf("moved to (%d,%d)
", ans[r1][c1]/BIG, ans[r1][c1]%BIG);
    }
}
return 0;
}

　　另一个思路是将所有操作保存，然后对于每个查询重新执行每个操作，但不需要计算整 个电子表格的变化，而只需关注所查询的单元格的位置变化。对于题目给定的规模来说，这 个方法不仅更好写，而且效率更高。代码如下：

#include<stdio.h>
#include<string.h>
#define maxd 10000
struct Command {
    char c[5];
    int r1, c1, r2, c2;
    int a, x[20];
} cmd[maxd];
int r, c, n;
int simulate(int* r0, int* c0) {
    for(int i = 0; i < n; i++) {
        if(cmd[i].c[0] == 'E') {
            if(cmd[i].r1 == *r0 && cmd[i].c1 == *c0) { *r0 = cmd[i].r2; *c0 = cmd[i].c2; }
            else if(cmd[i].r2 == *r0 && cmd[i].c2 == *c0) { *r0 = cmd[i].r1; *c0 = cmd[i].c1; }
        } 
        else {
            int dr = 0, dc = 0;
            for(int j = 0; j < cmd[i].a; j++) {
                int x = cmd[i].x[j];
                    if(cmd[i].c[0] == 'I') {
                        if(cmd[i].c[1] == 'R' && x <= *r0) dr++;
                        if(cmd[i].c[1] == 'C' && x <= *c0) dc++;
                    }
                    else {
                        if(cmd[i].c[1] == 'R' && x == *r0) return 0;
                        if(cmd[i].c[1] == 'C' && x == *c0) return 0;
                        if(cmd[i].c[1] == 'R' && x < *r0) dr--;
                        if(cmd[i].c[1] == 'C' && x < *c0) dc--;
                    }
            }        
        *r0 += dr; *c0 += dc;
        }
    }
    return 1;
}
int main() {
    int r0, c0, q, kase = 0;
    while(scanf("%d%d%d", &r, &c, &n) == 3 && r) {
        for(int i = 0; i < n; i++) {
            scanf("%s", cmd[i].c);
            if(cmd[i].c[0] == 'E') {
                scanf("%d%d%d%d", &cmd[i].r1, &cmd[i].c1, &cmd[i].r2, &cmd[i].c2);
            } 
            else {
                scanf("%d", &cmd[i].a);
                for(int j = 0; j < cmd[i].a; j++) scanf("%d", &cmd[i].x[j]);
            }
        }
        if(kase > 0) printf("
");
        printf("Spreadsheet #%d
", ++kase);
        scanf("%d", &q);
        while(q--) {
            scanf("%d%d", &r0, &c0);
            printf("Cell data in (%d,%d) ", r0, c0);
            if(!simulate(&r0, &c0)) printf("GONE
");
            else printf("moved to (%d,%d)
", r0, c0);
        }
    }
    return 0;
}