长度为n的环状串有n种表示法,分别为从某 个位置开始顺时针得到。例如,图3-4的环状串 有10种表示:
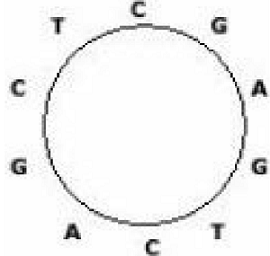
CGAGTCAGCT,GAGTCAGCTC,AGTCAGCTCG等。
在这些表示法中,字典序最小的称 为"最小表示"。 输入一个长度为n(n≤100)的环状DNA串(只包含A、C、G、T这4种字符)的一种表示法,你的任务是输出该环状串的最小表示。
例如,CTCC的最小表示是 CCCT,CGAGTCAGCT的最小表示为AGCTCGAGTC。
【分析】
本题出现了一个新概念:字典序。所谓字典序,就是字符串在字典中的顺序。一般地, 对于两个字符串,从第一个字符开始比较,当某一个位置的字符不同时,该位置字符较小的串,字典序较小(例如,abc比bcd小);如果其中一个字符串已经没有更多字符,但另一个字符串还没结束,则较短的字符串的字典序较小(例如,hi比history小)。字典序的概念可 以推广到任意序列,例如,序列1, 2, 4, 7比1, 2, 5小。 学会了字典序的概念之后,本题就不难解决了:就像"求n个元素中的最小值"一样,用变量ans表示目前为止,字典序最小串在输入串中的起始位置,然后不断更新ans。
#include<cstdio> #include<cstring> #define maxn 105 using namespace std; int ans[maxn];//ans数组含义:在y处存了y的最小生成元 bool less(char *s,int p,int q){ int n=strlen(s); for(int i=0;i<n;i++){ if(s[(p+i)%n]!=s[(q+i)%n]) return s[(p+i)%n]<s[(q+i)%n]; } return 0;//相等 } int main(){ char s[maxn]; scanf("%s",s); int ans=0; int n=strlen(s); for(int i=0;i<n;i++){ if(less(s,i,ans)) ans=i; } for(int i=0;i<n;i++){ putchar(s[(i+ans)%n]); } putchar(' '); return 0; }
注意环状在数据结构上的表示!!