网上已经有很多大佬总结得很好了,我就直接转发膜拜一发。
入门讲解博客Small_Orange_glory大佬的讲解,单点更新,区间查询,带图挺好理解
进阶讲解博客园cc123321大佬的讲解,区间修改,单点查询;区间修改,区间查询,写得很明朗
总结讲解博客园胡小兔大佬的讲解,所有操作都讲了一遍,还附带了二维的树状数组(还没学,留个坑)
耐心看完这三位大佬的博客,我想理解树状数组并不难。其实树状数组并不难,但第一次遇到时,自己心气浮躁,不能静下心去好好学习一下,学习还是得静心,戒骄戒躁。当然光看懂就是不行的,还是得会用,这里拉几题练练手。
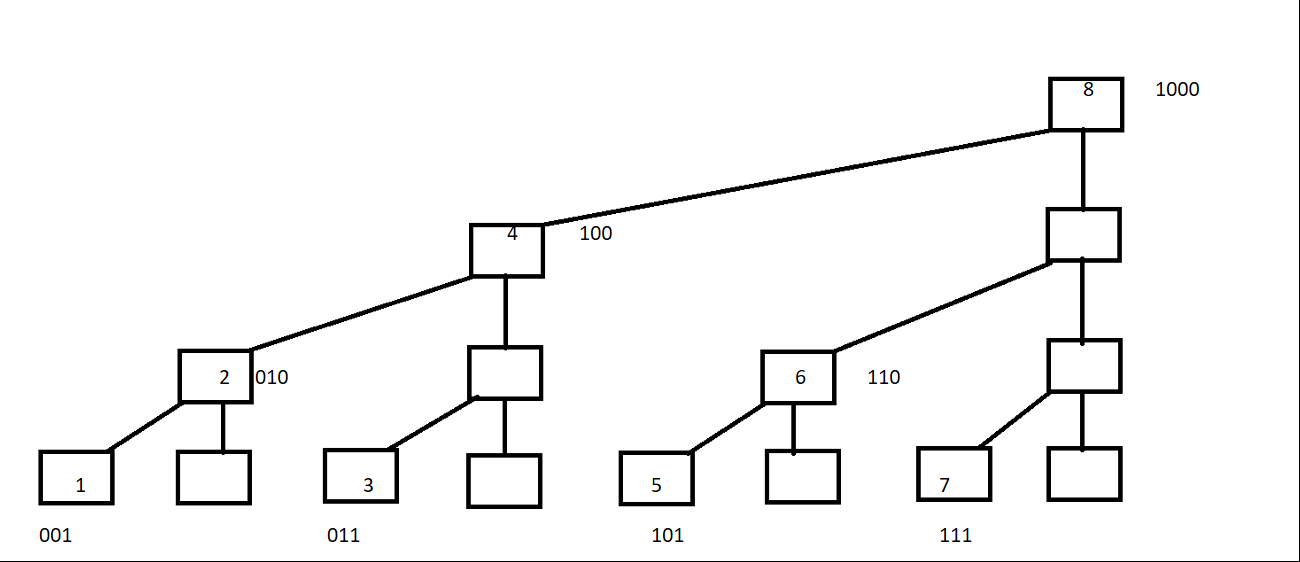
不得不说,整出树状数组的那个人真是神奇,虽然说有些线段树的操作。树状数组做不了,但是在都能做的操作下,树状数组不管是效率还是实现都快得多。我个人感觉树状数组是一个二进制和树结构的结合,lowbit就相当于树中每个节点相连的边,当要更新某个节点的信息时,受它影响的节点的信息也同步更新。像这个看这个简单的丑丑的上图,我们要求a数组区间1~4的和的话,也就是a1+a2+a3+a4时,不就是求c4吗,所以更新a1时同步的c2,c4也更新,a1+lowbit(a1)其实就可以看成a1和c2的连线。而当我们要求a1+a2+a3时,也就是求c2+a3,这时a3-lowbit(a3)可以看出a3和c2连的一条虚线(忘了画了,假装有的样子)。lowbit(x)的本质是什么,x最尾部1所代表的数,也就是2k(k就是尾部0的长度)。+lowbit的话从下图中体现就是,一直斜着向上到最近的节点(看1到2到4到8)(产生影响),-lowbit就是反过来的斜着向上到最近的节点(看7到6到4)(统计权值,因为像6不能由4加lowbit转移过来,所以4中的修改,6是不受4影响的,所以我们要统计前7个数的加和时就是节点7把在它之前没有对它产生影响的节点权值加上)。

#include<cstdio> #define ll long long #define lowbit(x) x&(-x) const int N=520118; int n,m,op; long a[N]={0}; void updata(int x,ll y) { while(x<=n) { a[x]+=y; x+=lowbit(x); } } ll getsum(int x) { ll ans=0; while(x) { ans+=a[x]; x-=lowbit(x); } return ans; } int main() { ll x,y; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) { scanf("%lld",&x); updata(i,x); } while(m--) { scanf("%d%lld%lld",&op,&x,&y); if(op==1) updata(x,y); else printf("%lld ",getsum(y)-getsum(x-1)); } return 0; }
我们在做单点更新区间查询时,就是把a数组当成叶子节点,然后求sum数组,所以现在单点查询的话,我们就可以把a数组当成sum数组,也就是另一个数组的前n项和,假设a[i]=a[i-1]+b[i]的话,那么a[i[不就是b[i[的前n项和了。所以我们把b[i]用树状数组表示出来,查询a[i]就是查询b[1]+b[2]+b[3]+b[4]+。。+b[i](a[i]的单点查询就是b[1]~b[i]的区间查询),然后区间修改呢,我们要想在a数组的,[l,r]这样一个区间里的每个a[i]都加x的话。我们看,a[l]=b[1]+b[2]+b[3]+..+b[l],a[l+1]=b[1]+b[2]+b[3]+..+b[l]+b[l+1],a[r]=b[1]+b[2]+b[3]+..+b[l]+b[l+1]+..+b[r],所以只要在b[l]处加上x,那么对后面的a[l],a[l+1]..a[r}都产生了加x的影响,那么怎么不对后面的产生影响呢,很简单,在b[r+1]处加上个-x就可以了(a[i]~a[j]的区间修改就是b[i]和b[j+1]的单点更新)

#include<cstdio> #define lowb(x) x&(-x) #define ll long long const int N=520118; ll a[N]={0},b[N]={0}; int n,m; void updata(int x,ll y) { while(x<=n) { b[x]+=y; x+=lowb(x); } } void modify(int x,int y,ll z) { updata(x,z); updata(y+1,-z); } ll geta(int x) { ll ans=0; while(x) { ans+=b[x]; x-=lowb(x); } return ans; } int main() { ll k; int x,y,op; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",&a[i]); while(m--) { scanf("%d%d",&op,&x); if(op==1) { scanf("%d%lld",&y,&k); modify(x,y,k); } else printf("%lld ",geta(x)+a[x]); } return 0; }
现在我们要求区间a[1]~a[i]的和,因为a[i]是b[i]的前n项和,那么a[1]+..+a[i]=b[1]+b[1]+b[2]+b[1]+b[2]+b[3]+...+b[1]+..+b[i]=i*b[1]+(i-1)*b[2]+(i-2)*b[3]+...+b[i],那怎么用树状数组表示出来呢,我们把公式转换一下就是,k*(b[1]+b[2]+b[3]+..b[i])-(0*b[1]+1*b[2]+2*b[3]+..+(i-1)*b[i])),b[1]+b[2]+b[3]+..+b[i]不难求吧,就是b[1]~b[i]的区间查询,然后后面部分呢,我们让c[i]=(i-1)*b[i],这时候把c[i]用树状数组表示出来,后面部分就是c[1]~c[i]的区间查询。可能会对c[i]的更新有疑惑,这里说一下,加入b[i]一开始是y,那么c[i[就是(i-1)*y,这时b[i]加上x,那么c[i]也得更新,也就是c[i]加上(i-1)*x,然后b[i]变成了x+y,c[i]变成了(i-1)(x+y),完美同步更新

1 #include<cstdio> 2 #define ll long long 3 #define lowb(x) x&(-x) 4 const int N=100118; 5 char op[3]; 6 ll n,m,a[N]={0},b[N]={0},c[N]={0}; 7 void updata(ll q[],ll x,ll y) 8 { 9 while(x<=n) 10 { 11 q[x]+=y; 12 x+=lowb(x); 13 } 14 } 15 ll geta(ll q[],ll x) 16 { 17 ll ans=0; 18 while(x) 19 { 20 ans+=q[x]; 21 x-=lowb(x); 22 } 23 return ans; 24 } 25 void modify(ll x,ll y,ll z) 26 { 27 updata(b,x,z); 28 updata(b,y+1,-z); 29 updata(c,x,(x-1)*z); 30 updata(c,y+1,-y*z); 31 } 32 ll getsum(ll x,ll y) 33 { 34 ll ans=0; 35 ans+=y*geta(b,y)-geta(c,y); 36 ans-=(x-1)*geta(b,x-1)-geta(c,x-1); 37 return ans; 38 } 39 int main() 40 { 41 scanf("%lld%lld",&n,&m); 42 for(int i=1;i<=n;i++) 43 { 44 scanf("%lld",&a[i]); 45 updata(b,i,a[i]-a[i-1]); 46 updata(c,i,(i-1)*(a[i]-a[i-1])); 47 } 48 ll x,y,z; 49 while(m--) 50 { 51 scanf("%s%lld%lld",op,&x,&y); 52 if(op[0]=='Q') 53 printf("%lld ",getsum(x,y)); 54 else 55 { 56 scanf("%lld",&z); 57 modify(x,y,z); 58 } 59 } 60 return 0; 61 }
