POJ

POJ - 1155TELE

　题目大意：有n个节点，电视台节点1转播一场比赛，会转播给其他转播点（2~n-m）或者是其他用户（n-m+1~n）,同时转播点也一样会转播给其他未被转播点或者用户，每个转播的连接都需要一定的费用，而每个用户也会支付一定的钱来观看比赛，问在不亏本去情况下，最多能转播几个用户?

　树形dp从题目的描述中就可得出一个树形结构，照理先画图理解和推导。

　

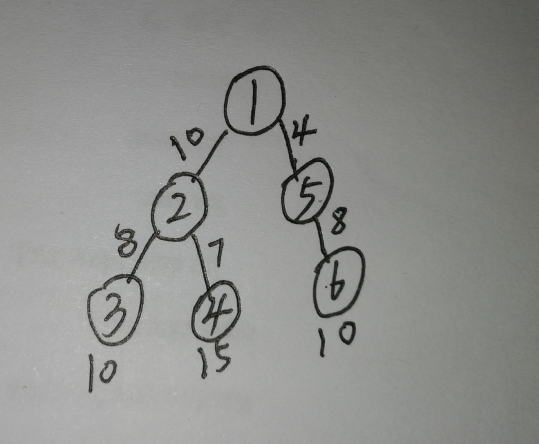
　　用户肯定就是叶子节点了，然后我们观察会发现，如果单纯的dp路径上的花费是很难做到的，像转播给3肯定是花费18，但此时再转播给4就只需要额外花费7就行了，无需再花费在1和2连接上的10.所以我们想要保留一个客户的话，那它的父节点也得保留，同时还得考虑它的父节点是否已经是为其他用户保留了，这是个比较难处理的地方。不过由这个留不留，要不要，我们可以想到什么？没错就是背包。那这题就是和二叉苹果树一样的思路了，dp[i][j]就表示i节点保存j个用户的最大收益值（负数的话就是亏损了），具体怎么做呢？

　　首先我们把每个点设为根节点的话，肯定统计得它的所有分支里有一共多少用户，在有新的分支时，然后遍历所有能保留的数目i个，在新分支保留j个用户时，已经遍历的部分就是保留I-j个用户，例如2节点的左边已经遍历了，dp[2][1]就等于10-8=2，然后这时4节点要加入，这时2节点就能保留两个客户了，并且有类似dp[2][2]=max(dp[2][2],dp[2][1]+dp[4][1]),dp[2][1]=max(dp[2][1],dp[2][0]+dp[4][1])这样的转移，转移方程就是

dp[u][i]=max(dp[u][i],dp[u][i-j]+dp[v][j])(u节点保留p个用户,已经遍历的部分保留i-j个用户，新加入的子节点保留j个用户）

　　从而我们可以得到2节点保留1个用户，2个用户的最大收益，当然最后2的所有分支加入完后不管是dp[2][1]还是dp[2][2]都得减去和1的连接的花费10。同理到其他节点也是一样的处理，最后我们再在1节点由所有用户数从后往前找到第一个收益不是负数的答案。详情见代码。

　　

#include<cstdio>
#include<cstring>
#include<algorithm> 
using namespace std;
const int N=3003;
struct Side{
    int v,ne,cost;
}S[N*N];
int sn,n,m,head[N],pay[N],man[N],dp[N][N];
void add(int u,int v,int c)
{
    S[sn].v=v;
    S[sn].cost=c;
    S[sn].ne=head[u];
    head[u]=sn++;
}
void dfs(int u,int cost)//cost连接父节点的花费 
{
    for(int i=head[u];i!=-1;i=S[i].ne)
    {
        int v=S[i].v;
        dfs(v,S[i].cost);
        man[u]+=man[v];//统计用户人数 
        for(int i=man[u];i>=1;i--)//类似01背包的原地滚动
        //如果是从1到man[u],dp[u][i]会被已经更新的dp[u][i-j]影响 
            for(int j=1;j<=man[v]&&j<=i;j++)
                dp[u][i]=max(dp[u][i],dp[u][i-j]+dp[v][j]);
            //当前保留i个用户，已经遍历过的部分保留i-j个，新加入的分支保留j个 
    }
    for(int i=1;i<=man[u];i++)
        dp[u][i]+=pay[u]-cost;//所有情况都加上支付的钱减去连接到父节点的花费 
    //用户外的其他节点的pay为0,只有根节点的cost为0 
}
int main()
{
    int k,a,c;
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=0;i<=n-m;i++)
        {
            head[i]=-1;
            pay[i]=0;//非用户节点支付为0 
            man[i]=0;//并且初始没有用户 
            dp[i][0]=0; 
            for(int j=1;j<=m;j++)//要更新收益最大值，初始化为负的最大值 
                dp[i][j]=-0x3f3f3f3f;
        }
        for(int i=n-m+1;i<=n;i++)
        {
            head[i]=-1; 
            man[i]=1;//用户一开始自己算一个 
            dp[i][1]=0;//用户节点不需要更新，初始化为0 
        }
        sn=0;
        for(int i=1;i<=n-m;i++)
        {
            scanf("%d",&k);
            while(k--)
            {
                scanf("%d%d",&a,&c);
                add(i,a,c);
            }
        }
        for(int i=n-m+1;i<=n;i++)//从用户的编号开始 
            scanf("%d",&pay[i]);
        dfs(1,0);
        for(int i=m;i>=0;i--)//从最大用户数倒过来遍历 
            if(dp[1][i]>=0)//保留用户时不亏损就是答案 
            {
                printf("%d
",i);
                break;
            }
    }
    return 0;
}